Energie tworzenia wiązań jonowych

wiązania jonowe powstają, gdy dodatnio i ujemnie naładowane jony są utrzymywane razem przez siły elektrostatyczne. Rozważmy pojedynczą parę jonów, jeden kation i jeden anion. Jak silna będzie siła ich przyciągania? Zgodnie z Prawem Coulomba energia przyciągania elektrostatycznego (\(e\)) pomiędzy dwoma naładowanymi cząstkami jest proporcjonalna do wielkości ładunków i odwrotnie proporcjonalna do odległości między jądrami (\(r\)):

\

\

gdzie ładunek każdego jonu jest reprezentowany przez symbol Q. stała proporcjonalności k jest równa 2,31 × 10-28 J·M. ta wartość k obejmuje ładunek pojedynczego elektronu (1,6022 × 10-19 C) dla każdego jonu. Równanie można również zapisać za pomocą ładunku każdego jonu, wyrażonego w kulombach (C), włączonych do stałej. W tym przypadku stała proporcjonalności, k, wynosi 8,999 × 109 J·m/C2. W podanym przykładzie Q1 = +1(1,6022 × 10-19 C) i Q2 = -1(1,6022 × 10-19 C). Jeśli Q1 i Q2 mają przeciwne znaki (jak w NaCl, na przykład, gdzie Q1 jest +1 dla Na+ I Q2 jest -1 dla Cl−), to E jest ujemne, co oznacza, że energia jest uwalniana, gdy przeciwstawnie naładowane jony są połączone ze sobą z nieskończonej odległości, tworząc izolowaną parę jonów.

energia jest zawsze uwalniana podczas tworzenia wiązania i odpowiednio, zawsze wymaga energii do zerwania wiązania.

Jak pokazuje Zielona krzywa w dolnej połowie rysunku \(\PageIndex{1}\), maksymalna energia zostanie uwolniona, gdy jony będą nieskończenie blisko siebie, przy r = 0. Ponieważ jony zajmują przestrzeń i mają strukturę z dodatnim jądrem otoczonym przez elektrony, nie mogą one być nieskończenie blisko siebie. Przy bardzo krótkich odległościach oddziaływania elektron-elektron pomiędzy elektronami na sąsiednich jonach stają się silniejsze niż oddziaływania atrakcyjne między jonami o przeciwnych ładunkach, co pokazuje czerwona krzywa w górnej połowie rysunku \(\PageIndex{1}\). Całkowita energia układu jest równowagą między atrakcyjnymi i odpychającymi oddziaływaniami. Fioletowa krzywa na rysunku \(\PageIndex{1}\) pokazuje, że całkowita energia układu osiąga minimum w r0, punkcie, w którym elektrostatyczne odpychanie i przyciąganie są dokładnie zrównoważone. Odległość ta jest taka sama jak doświadczalnie zmierzona odległość wiązania.

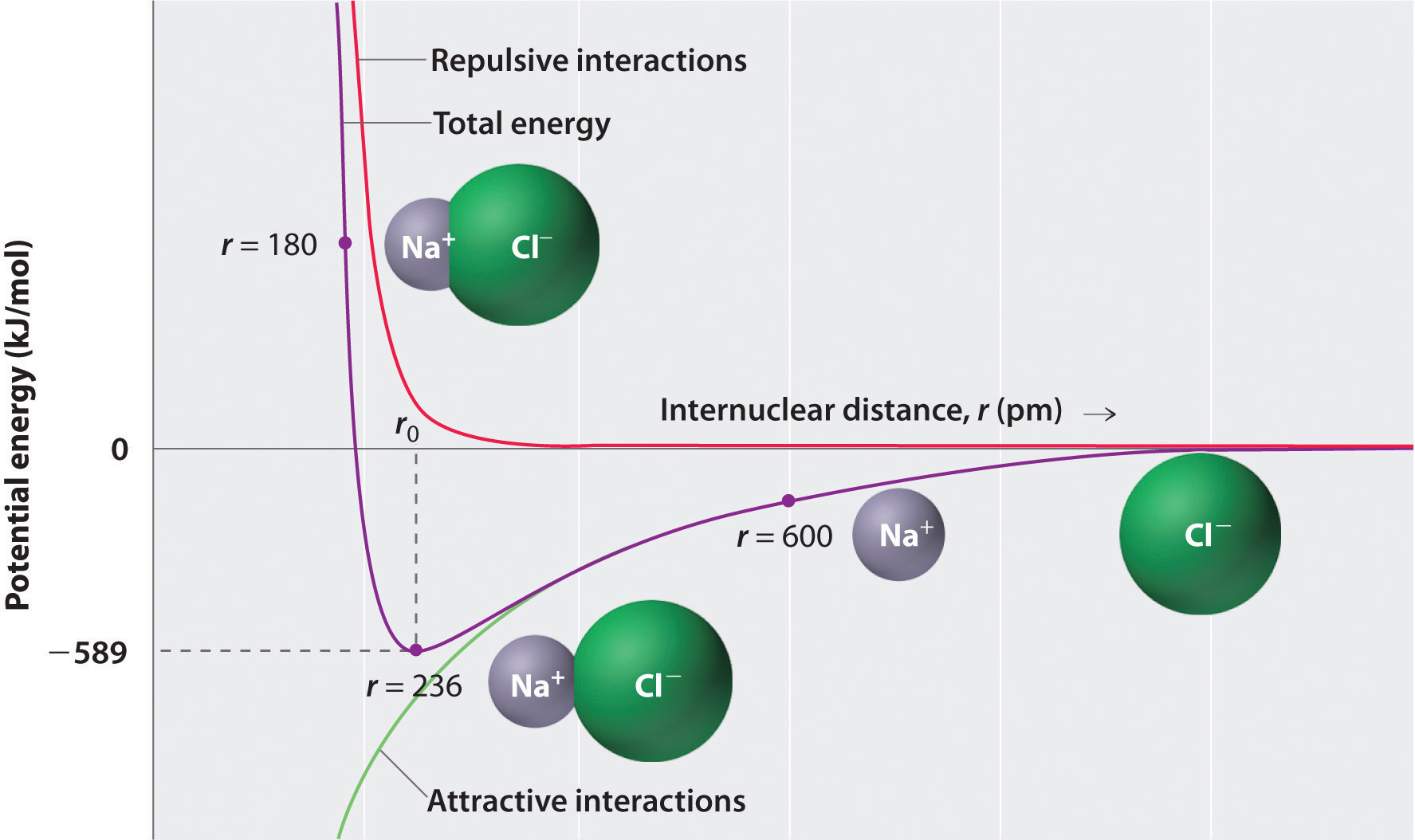
rozważmy energię uwolnioną, gdy jon gazowy \(Na^+\) i Jon gazowy \(Cl^-\) są połączone z r = ∞ do r = R0. Biorąc pod uwagę, że obserwowana odległość między jądrami w fazie gazowej wynosi 236 pm, zmiana energii związana z utworzeniem pary jonów z jonu \(na^+_{(G)}\) i jonu \(CL^-_{(g)}\) jest następująca:

\ &= (2.31 \times {10^ {- 28}}\RM{J}\cdot \cancel{m} ) \left( \dfrac{( + 1)( – 1)}{236\; \cancel{pm} \ times 10^{ – 12} \cancel{M/pm}} \ right) \ \ & = – 9.79\ times 10^{ – 19}\; j / ion\; pair \ label{Eq2} \ end{align*}\]

ujemna wartość wskazuje, że energia została uwolniona. Nasza konwencja jest taka, że jeśli proces chemiczny dostarcza energii światu zewnętrznemu, zmiana energii jest negatywna. Jeśli wymaga energii, zmiana energii jest pozytywna. Aby obliczyć zmianę energii w tworzeniu mola par NaCl, musimy pomnożyć energię na parę jonów przez liczbę Avogadro:

\

jest to energia uwalniana, gdy powstaje 1 mol par jonów gazowych, a nie Gdy 1 mol jonów dodatnich i ujemnych skrapla się, tworząc siatkę krystaliczną. Ze względu na dalekie oddziaływania w strukturze sieci, energia ta nie odpowiada bezpośrednio energii sieci krystalicznej ciała stałego. Jednak duża wartość ujemna wskazuje, że łączenie jonów dodatnich i ujemnych jest energetycznie bardzo korzystne, niezależnie od tego, czy powstaje para jonów, czy siatka krystaliczna.

podsumowujemy ważne punkty dotyczące wiązania jonowego:

• przy r0 jony są bardziej stabilne (mają mniejszą energię potencjalną) niż w nieskończonej odległości międzyjądrowej. Gdy przeciwstawnie naładowane jony są połączone od R = ∞ do r = r0, energia układu jest obniżana (energia jest uwalniana).
• ze względu na niską energię potencjalną w r0, energia musi zostać dodana do układu, aby oddzielić jony. Ilość potrzebnej energii to energia wiązania.
• energia układu osiąga minimum w określonej odległości międzyprocesorowej (odległości wiązania).