proszę podać Liczby oddzielone przecinkiem do obliczenia.

powiązane Kalkulator statystyk | Kalkulator odchylenia standardowego | Kalkulator wielkości próbki

Średnia

słowo mean, które jest homonimem dla wielu innych słów w języku angielskim, jest podobnie niejednoznaczne nawet w dziedzinie matematyki. W zależności od kontekstu, czy to matematycznego, czy statystycznego, co rozumie się przez „średnie” zmiany. W najprostszej definicji matematycznej dotyczącej zbiorów danych, średnia używana jest średnia arytmetyczna, zwana również oczekiwaniem matematycznym lub średnią. W tej postaci średnia odnosi się do wartości pośredniej między dyskretnym zbiorem liczb, a mianowicie do sumy wszystkich wartości w zbiorze danych, podzielonej przez całkowitą liczbę wartości. Równanie do obliczania średniej arytmetycznej jest praktycznie identyczne z równaniem do obliczania pojęć statystycznych populacji i średniej próby, z niewielkimi różnicami w używanych zmiennych:

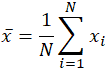
średnia jest często oznaczana jako X, wymawiana „X bar”, a nawet w innych zastosowaniach, gdy zmienna nie jest x, notacja słupkowa jest częstym wskaźnikiem jakiejś formy średniej. W konkretnym przypadku średniej populacji, zamiast używać zmiennej x, stosuje się grecki symbol mu lub μ. Podobnie, a raczej myląco, średnia próby w statystykach jest często oznaczana dużą literą X. Biorąc pod uwagę zestaw danych 10, 2, 38, 23, 38, 23, 21, zastosowanie sumowania powyżej plonów:

jak wcześniej wspomniano, jest to jedna z najprostszych definicji średniej, a niektóre inne obejmują ważoną średnią arytmetyczną (która różni się tylko tym, że niektóre wartości w zbiorze danych przyczyniają się do większej wartości niż inne) i średnią geometryczną. Właściwe zrozumienie danych sytuacji i kontekstów często może dostarczyć osobie narzędzi niezbędnych do określenia, jaką statystycznie istotną metodę zastosować. Ogólnie rzecz biorąc, średnia, mediana, tryb i zakres powinny idealnie Wszystkie być obliczane i analizowane dla danej próbki lub zestawu danych, ponieważ wyjaśniają różne aspekty danych, a jeśli rozpatrywane samodzielnie, może prowadzić do błędnych przedstawień danych, jak zostanie wykazane w następujących sekcjach.

Mediana

koncepcja statystyczna mediany jest wartością, która dzieli próbkę danych, populację lub rozkład prawdopodobieństwa na dwie połowy. Znalezienie mediany zasadniczo polega na znalezieniu wartości w próbce danych, która ma fizyczną lokalizację między resztą liczb. Należy zauważyć, że przy obliczaniu mediany skończonej listy liczb, kolejność próbek danych jest ważna. Konwencjonalnie, wartości są wymienione w porządku rosnącym, ale nie ma prawdziwego powodu, że Wymienianie wartości w porządku malejącym dałoby różne wyniki. W przypadku, gdy całkowita liczba wartości w próbce danych jest nieparzysta, mediana jest po prostu liczbą w środku listy wszystkich wartości. Gdy próbka danych zawiera parzystą liczbę wartości, mediana jest średnią z dwóch średnich wartości. Chociaż może to być mylące, po prostu pamiętaj, że nawet jeśli mediana czasami obejmuje obliczenie średniej, gdy ten przypadek powstaje, będzie to obejmować tylko dwie wartości środkowe, podczas gdy średnia obejmuje wszystkie wartości w próbce danych. W nieparzystych przypadkach, gdy istnieją tylko dwie próbki danych lub istnieje parzysta liczba próbek, w których wszystkie wartości są takie same, średnia i mediana będą takie same. Biorąc pod uwagę ten sam zestaw danych, co poprzednio, mediana zostanie uzyskana w następujący sposób:

2,10,21,23,23,38,38

Po wymienieniu danych w kolejności rosnącej i ustaleniu, że istnieje Nieparzysta liczba wartości, jasne jest, że mediana 23 jest w tym przypadku. Jeśli do zestawu danych dodano inną wartość:

2,10,21,23,23,38,38,1027892

ponieważ istnieje parzysta liczba wartości, mediana będzie średnią dwóch średnich liczb, w tym przypadku 23 i 23, których średnia wynosi 23. Należy zauważyć, że w tym konkretnym zbiorze danych dodanie wartości odstającej (wartości znacznie wykraczającej poza oczekiwany zakres wartości), wartość 1,027,892, nie ma rzeczywistego wpływu na zestaw danych. Jeśli jednak średnia jest obliczana dla tego zestawu danych, wynik wynosi 128,505. 875. Ta wartość wyraźnie nie jest dobrą reprezentacją siedmiu innych wartości w zbiorze danych, które są znacznie mniejsze i bliższe wartości niż średnia i odstająca. Jest to główna zaleta wykorzystania mediany w opisywaniu danych statystycznych w porównaniu ze średnią. Podczas gdy oba, jak również inne wartości statystyczne, powinny być obliczane przy opisywaniu danych, jeśli można użyć tylko jednej, mediana może zapewnić lepsze oszacowanie typowej wartości w danym zbiorze danych, gdy występują bardzo duże różnice między wartościami.

tryb

w statystykach tryb jest wartością w zbiorze danych, która ma największą liczbę powtórzeń. Możliwe jest, że zbiór danych jest multimodalny, co oznacza, że ma więcej niż jeden tryb. Na przykład:

2,10,21,23,23,38,38

oba 23 i 38 pojawiają się dwa razy, co czyni je trybem dla powyższego zestawu danych.

podobnie jak średnia i mediana, tryb jest używany jako sposób wyrażania informacji o zmiennych losowych i populacjach. W przeciwieństwie jednak do średniej i mediany, tryb ten jest koncepcją, którą można zastosować do wartości nie numerycznych, takich jak marka chipsów tortilla najczęściej kupowanych w sklepie spożywczym. Na przykład, porównując marki Tostitos, Mission i XOCHiTL, jeśli okaże się, że w sprzedaży chipsów tortilla, XOCHiTL jest trybem i sprzedaje w stosunku 3:2:1 w porównaniu odpowiednio do chipsów tortilla marki tostitos i Mission, stosunek ten może być użyty do określenia, ile torebek każdej marki do zapasów. W przypadku, gdy w danym okresie sprzedają się 24 Torebki chipsów tortilla, sklep będzie zaopatrywał 12 torebek chipsów XOCHiTL, 8 Tostitos i 4 Mission, jeśli korzystasz z tego trybu. Jeśli jednak sklep po prostu używał średniej i sprzedawał 8 torebek każdego, może potencjalnie stracić 4 sprzedaż, jeśli klient pożądał tylko żetonów XOCHiTL, a nie żadnej innej marki. Jak wynika z tego przykładu, ważne jest, aby wziąć pod uwagę wszystkie sposoby wartości statystycznych przy próbie wyciągnięcia wniosków na temat dowolnej próbki danych.

zakres

zakres zbioru danych w statystykach jest różnicą między największą i najmniejszą wartością. Podczas gdy zakres ma różne znaczenia w różnych dziedzinach statystyki i matematyki, jest to jego najbardziej podstawowa definicja i jest to, co jest używane przez dostarczony Kalkulator. W tym samym przykładzie:

2,10,21,23,23,38,38
38 – 2 = 36

zakres w tym przykładzie wynosi 36. Podobnie jak średnia, zakres może mieć znaczący wpływ na bardzo duże lub małe wartości. Używając tego samego przykładu co poprzednio: