Articles

łatwe permutacje i kombinacje

by admin

zawsze myliłem „permutację” i „kombinację” – która jest która?

Oto prosty sposób na zapamiętanie: permutacja brzmi skomplikowanie, prawda? I tak jest. W przypadku permutacji liczy się każdy szczegół. Alice, Bob and Charlie różni się od Charlie, Bob and Alice (wpisz tutaj imiona znajomych).

kombinacje, z drugiej strony, są dość łatwe. Szczegóły nie mają znaczenia. Alice, Bob i Charlie to to samo co Charlie, Bob i Alice.

permutacje są dla list (kolejność ma znaczenie) i kombinacji są dla grup (kolejność nie ma znaczenia).

wiesz, „zamek szyfrowy” powinien być naprawdę nazywany „blokadą permutacji”. Kolejność umieszczania liczb ma znaczenie.

łatwe permutacje i kombinacje

prawdziwy „zamek szyfrowy” zaakceptowałby zarówno 10-17-23, jak i 23-17-10 jako poprawne.

permutacje: szczegóły

Zacznijmy od permutacji, czyli wszystkich możliwych sposobów robienia czegoś. Używamy wymyślnego terminu „permutacja”, więc będziemy dbać o każdy szczegół, w tym o kolejność każdego elementu. Powiedzmy, że mamy 8 osób:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

na ile sposobów możemy przyznać nagrodę za 1, 2 i 3 miejsce wśród ośmiu uczestników? (Złoto / Srebro / brąz)

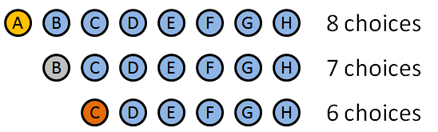
permuacja przykładowe medale

będziemy używać permutacji, ponieważ kolejność rozdawania tych medali ma znaczenie. Oto jak to się psuje:

  • złoty medal: 8: A B C D E F G H (sprytnie, jak udało mi się dopasować imiona do liter, co?). Powiedzmy, że a wygrywa złoto.
  • srebrny medal: 7: B C D E F G H. powiedzmy, że b zdobywa srebro.
  • brązowy medal: 6: C D E F G H. powiedzmy … C zdobywa brąz.

wybraliśmy pewne osoby, które wygrały, ale szczegóły nie mają znaczenia: na początku mieliśmy 8 wyborów, potem 7, potem 6. Całkowita liczba opcji wynosiła $8 * 7 * 6 = 336$.

przyjrzyjmy się szczegółom. Musieliśmy zamówić 3 osoby z 8. Aby to zrobić, zaczęliśmy od wszystkich opcji (8), a następnie zabieraliśmy je pojedynczo (7, następnie 6), aż skończyły się medale.

wiemy, że silnia jest:

\displaystyle{ 8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \ cdot 1 }

Niestety, to za dużo! Chcemy tylko $8 * 7 * 6$. Jak możemy „zatrzymać” silnię na 5?

w tym miejscu permutacje stają się fajne: zauważ, jak chcemy pozbyć się $5 * 4 * 3 * 2 * 1$. Jak inaczej to nazwać? 5 silnia!

więc jeśli zrobimy 8!/5! otrzymujemy:

\displaystyle{\frac{8!}{5!} = \frac{8 \ cdot 7 \ cdot 6 \ cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \ cdot 6}

i dlaczego użyliśmy liczby 5? Ponieważ pozostał po odebraniu 3 medali z 8. Więc lepszym sposobem na napisanie tego byłoby:

\displaystyle{\frac{8!}{(8-3)!}}

gdzie 8!/(8-3)! to tylko fantazyjny sposób na powiedzenie ” użyj pierwszych 3 liczb z 8!”. Jeśli mamy łącznie n pozycji i chcemy wybrać k w określonej kolejności, otrzymujemy:

\displaystyle{\frac{n!{(n-k)!}}

i to jest fantazyjna formuła permutacji: masz n elementów i chcesz znaleźć liczbę sposobów na zamówienie K elementów:

\displaystyle{P(n,k) = \frac{n!{(n-k)!}}

kombinacje są łatwe. Porządek nie ma znaczenia. Możesz to wymieszać i wygląda tak samo. Powiedzmy, że jestem skąpcem i nie stać mnie na oddzielne złote, srebrne i brązowe medale. Właściwie, stać mnie tylko na puste puszki.

na ile sposobów mogę dać 3 puszki 8 osobom?

cóż, w tym przypadku kolejność, którą wybieramy, nie ma znaczenia. Jeśli dam puszkę Alice, Bobowi, a potem Charliemu, to tak samo, jak dać Charliemu, Alice, a potem Bobowi. Tak czy inaczej, są równie rozczarowani.

to podnosi ciekawą kwestię-mamy tu kilka zwolnień. Alice Bob Charlie = Charlie Bob Alice. Przez chwilę zastanówmy się, na ile sposobów możemy przestawić 3 osoby.

Cóż, mamy 3 opcje dla pierwszej osoby, 2 dla drugiej i tylko 1 dla ostatniej. Więc mamy $3 * 2 * 1$ Sposoby Na ponowne zorganizowanie 3 osób.

chwila … to wygląda trochę jak permutacja! Oszukałeś mnie!

rzeczywiście. Jeśli masz N ludzi i chcesz wiedzieć, ile jest uzgodnień dla wszystkich z nich, to jest to po prostu N silnia lub N!

więc jeśli mamy 3 puszki do rozdania, to są 3! lub 6 wariacji dla każdego wyboru, który wybierzemy. Jeśli chcemy dowiedzieć się, ile kombinacji mamy, po prostu tworzymy wszystkie permutacje i dzielimy przez wszystkie nadmiarowości. W naszym przypadku otrzymujemy 336 permutacji (z góry) i dzielimy przez 6 redundancji dla każdej permutacji i otrzymujemy 336/6 = 56.

ogólny wzór to

\displaystyle{C(n,k) = \frac{P(n,k)}{K!}}

co oznacza „Znajdź wszystkie sposoby na wybranie K osób z n i podziel przez k! warianty”. Pisząc to, otrzymujemy nasz wzór kombinacji, czyli liczbę sposobów łączenia elementów k ze zbioru n:

\displaystyle{C(n,k) = \frac{n!{(n-k)!k!}}

czasami C(n,k) zapisuje się jako:

\displaystyle{\binom {n}{k}}

co jest współczynnikiem dwumianowym.

kilka przykładów

oto kilka przykładów kombinacji (kolejność nie ma znaczenia) z permutacji (kolejność ma znaczenie).

  • połączenie: wybór zespołu 3-osobowego z grupy 10-osobowej. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    permutacja: wybór prezesa, wiceprezesa i Waterboya z grupy 10. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • połączenie: wybór 3 deserów z menu 10. C (10,3) = 120.

    permutacja: Lista 3 ulubionych deserów, w kolejności, z menu 10. P (10,3) = 720.

nie zapamiętywaj formuł, zrozum, dlaczego działają. Kombinacje brzmią prościej niż permutacje i są. Masz mniej kombinacji niż permutacji.

inne posty z tej serii

  1. łatwe permutacje i kombinacje
  2. nawigacja po siatce za pomocą kombinacji i permutacji
  3. Jak rozumieć kombinacje za pomocą mnożenia
  4. dlaczego mnożymy kombinacje?