zal een oud probleem een nieuw inzicht opleveren? Misschien een elegant bewijs van de 4-kleurstelling?
het vierkleurenprobleem is een van de bekendste wiskundige problemen. Het verzette zich meer dan honderd jaar tegen bewijs voordat het uiteindelijk bezweek; uiteindelijk was er een geldig bewijs, maar een dat op meer dan duizend uur computertijd vertrouwde. Jim Tilley ‘ s onderzoek suggereert dat een dramatische vereenvoudiging uiteindelijk mogelijk zou kunnen zijn. Hij heeft een eigenschap ontdekt, Kempe-vergrendeling, die een minimum tegenvoorbeeld van de 4-kleurstelling moet vertonen en heeft een vermoeden geformuleerd, gebaseerd op uitgebreide onderzoeken, dat de Birkhoff-diamant de enige fundamentele Kempe-vergrendelingsconfiguratie is.
Grafiekkleuring omvat het toewijzen van labels, of kleuren, aan de hoekpunten van een wiskundig object dat een grafiek wordt genoemd. Het 4-kleurenprobleem vormde een van de oorspronkelijke motivaties voor de ontwikkeling van de algebraïsche grafietheorie. Grafiekkleuren wordt gebruikt in veel echte problemen, zoals het minimaliseren van conflicten bij het plannen van sportevenementen, het plannen van onderzoekroosters en het organiseren van zitplaatsplannen, zelfs voor CCTV-camera ‘ s in een gebouw met veel hoeken om cameraoverlapping te minimaliseren. Het biedt ook de basis voor Sudoku puzzels.
tegenwoordig wordt het vierkleurenprobleem uitgedrukt in grafieken, en in plaats van regio ‘ s in kaarten te kleuren, kleurt men hoekpunten in grafieken. Alle bestaande bewijzen van de 4-kleurstelling tonen aan dat een minimum tegenvoorbeeld niet kan bestaan. (Een minimum tegenvoorbeeld is de kleinste vlakke grafiek die meer dan Vier Kleuren vereist voor een juiste kleuring van de hoekpunten.) Alleen vlakke grafieken die driehoeken zijn hoeven te worden overwogen, aangezien elke grafiek die geen driehoeksmeting is, in één kan worden omgezet door randen in te voegen. Als de resulterende triangulatie 4-kleurig is, dan is de oorspronkelijke grafiek ook 4-kleurig. Het is zeer nuttig om je onderzoek te kunnen beperken tot driehoeken.

het zou een verbazingwekkende vereenvoudiging zijn als alleen de Birkhoff-diamant de sleutel is tot 4-kleurbaarheid. het eerste geldige bewijs werd in 1976 aangekondigd door Kenneth Appel en Wolfgang Haken. Het kostte meer dan duizend uur computertijd om bepaalde aspecten van hun argument te verifiëren. Deze notie van het vertrouwen op computercode, die mogelijk door de mens veroorzaakte fouten bevatten (en hun code deed!), in plaats van een’ menselijk ‘ bewijs, heeft niet voldaan aan een groot deel van de wiskundige gemeenschap. Appel en Haken ‘ s bewijs was elegant in de algemene structuur, maar de details waren lelijk. het bewijs werd in 1996 verfijnd door een team van vier wiskundigen: Robertson, Sanders, Seymour en Thomas, maar ze vertrouwden nog steeds op computercode om hun bewijs te vervolledigen. In 2010 bood Steinberger nog een variant aan. Er is echter nog steeds geen volledig bevredigend antwoord op de vraag waarom de 4-kleurstelling waar is. (Zodra het vermoeden werd bewezen, kreeg het de status van een ‘stelling.’)

en amateur wiskundige.
de zoektocht naar een alternatief bewijs
Het 4-kleurenprobleem is zo gemakkelijk te verwoorden en te begrijpen dat het de interesse heeft gewekt van vele duizenden amateur-wiskundigen, die allemaal geloven dat ze een eenvoudig klassiek bewijs kunnen vinden en zo beroemd kunnen worden. Jim Tilley ’s vader, een natuurkundige en directeur van Canada’ s Royal Military College van 1978-1984, was een dergelijke dromer. Wanneer hij voelde dat hij een doorbraak had gemaakt, vroeg hij zijn zoon, Jim, om zijn werk te controleren. Jim vond altijd een fout. Maar ondanks zijn aanvankelijke scepsis dat de inspanningen van zijn vader ooit vruchten zouden afwerpen, raakte hij besmet met een enthousiasme voor het 4-kleurenprobleem en begon het intensief te bestuderen.Jim Tilley ‘ s onderzoek leidde tot zijn ontdekking van een nieuwe eigenschap die een minimum tegenvoorbeeld van de 4-kleurstelling moet vertonen. Hij noemde het Kempe-locking.’Hij besefte dat het waarschijnlijk onverenigbaar was met een andere eigenschap die een minimum tegenvoorbeeld moet vertonen – namelijk., hoe verbonden een grafiek is (hoeveel hoekpunten moeten uit een grafiek worden verwijderd voordat deze uit elkaar valt).
Tilley ‘ s Kempe-locking is een eigenschap geassocieerd met een rand in een triangulatie. Het begrip begint met het verwijderen van een rand xy tussen aangrenzende hoekpunten x en y. Als voor elke 4-kleur van de resulterende grafiek waarin de kleuren van x en y gelijk zijn, er geen opeenvolging van kleur-wisselingen op Kempe kettingen is die ervoor zorgt dat de kleur van x verschilt van de kleur van y, dan wordt de oorspronkelijke triangulatie gezegd Kempe-vergrendeld te zijn ten opzichte van de rand xy. Tilley bewees dat een minimum tegenvoorbeeld van de 4-kleurstelling Kempe-vergrendeld moet zijn met betrekking tot elk van zijn randen; elke rand in een minimum tegenvoorbeeld moet deze kleuring eigenschap hebben.
Kempe-locking is een bijzonder beperkende voorwaarde waaraan moeilijker kan worden voldaan als een triangulatie groter wordt. Tilley ging uitzoeken of er iets gemeen is met driehoeken met Kempe-vergrendelde randen. Zijn eerste zoektocht naar Kempe-locking leidde hem naar de Birkhoff-diamant.

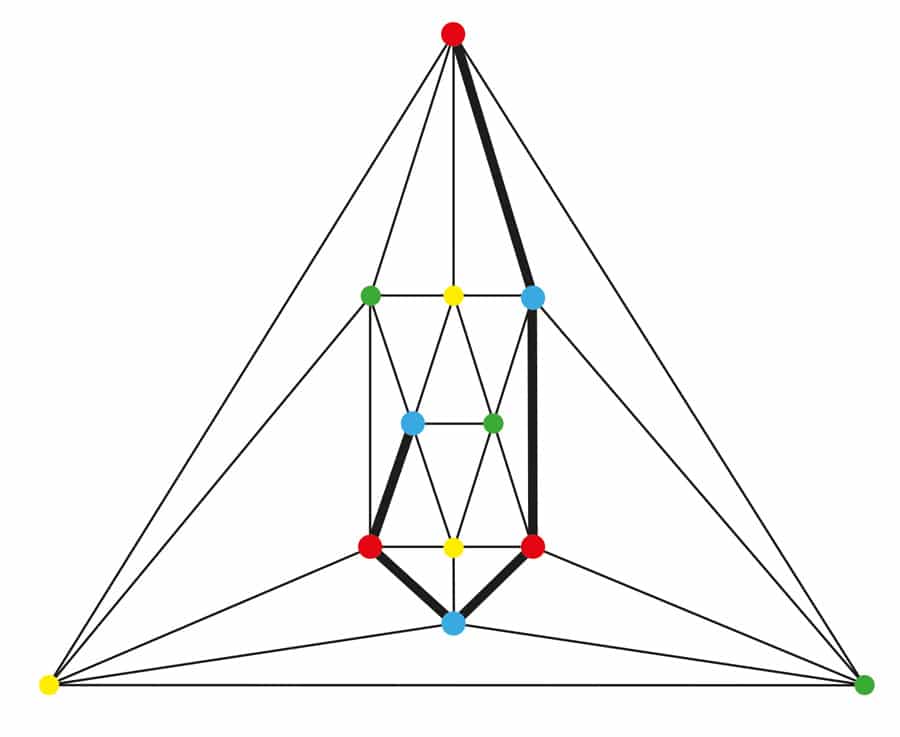
Figuur 3. Twee vlakke grafieken, één een 4-verbonden driehoeksmeting op 6 hoekpunten en één een 5-verbonden driehoeksmeting op 17 hoekpunten.
De Birkhoff-diamant
In 1913 ontdekte G. D. Birkhoff dat een bepaalde configuratie van tien landen in een kaart (een grensring van zes landen die een verzameling van vier landen omsluit) een belangrijke eigenschap heeft. Als die configuratie aanwezig is in een map en als de submap met die configuratie verwijderd 4-colourable is, dan zal de hele map 4-colourable zijn. Dus, een minimum tegenvoorbeeld kan die specifieke configuratie niet bevatten. Het is bekend geworden als de Birkhoff diamant. Tilley ontdekte dat een Kempe-locked edge xy alleen lijkt te ontstaan als x en y ook de eindpunten zijn van de graph – versie van een Birkhoff-diamant. Zie Figuur 2.
het vermoeden is gemakkelijk te verklaren, begrijpelijk en intrigerend, en biedt een overtuigende verklaring voor waarom alle planaire grafieken 4-kleurig zijn.
omdat hij geen Kempe-vergrendelingsconfiguratie zonder Birkhoff-diamant tegenkwam, vermoedde hij dat de Birkhoff-diamant de enige ‘fundamentele’ Kempe-vergrendelingsconfiguratie is, die geen kleinere Kempe-vergrendelingsconfiguratie als subgraph bevat. Tilley ontdekte echter dat hij zijn kritische vermoeden niet kon bewijzen. Het was frustrerend omdat, als het waar is, het vermoeden direct de 4-kleurstelling zou bewijzen. (Om een minimum tegenvoorbeeld te zijn, zou een triangulatie een Birkhoff diamond subgraph moeten bevatten, maar als dat zo was, zou het geen minimum tegenvoorbeeld kunnen zijn.)
een overweldigend ondersteunend geval
In plaats van zijn vermoeden te bewijzen, deed Tilley het volgende beste. Hij besloot om de rol van een experimentalist te spelen en een overweldigende zaak op te bouwen om zijn vermoeden te ondersteunen. Hij verdeelde alle relevante vlakke driehoeken in twee klassen: die waarin ten minste vier hoekpunten moeten worden verwijderd voordat de grafieken uit elkaar vallen (4-verbonden) en die waarin ten minste vijf hoekpunten moeten worden verwijderd voordat de grafieken uit elkaar vallen (5-verbonden). Zie Figuur 3. Nuttig in Tilley ‘ s uitgebreide zoektocht was dat hij slechts één lid van elke isomorfismeklasse moest onderzoeken (grafieken die structureel identiek zijn). Tilley onderzocht alle 8.044 isomorfismeklassen van 4-verbonden vlakke driehoeken op maximaal 15 hoekpunten en alle 9.733 isomorfismeklassen van 5-verbonden vlakke driehoeken op maximaal 24 hoekpunten. Hij vond slechts drie Kempe-vergrendelde driehoeken. Elke ontdekte Kempe-vergrendelde rand bevatte een Birkhoff diamant en elke vond plaats in een 4-verbonden driehoeksmeting. Er waren er helemaal geen Onder 5-verbonden driehoeken.

Tilley breidde zijn zoekopdracht uit tussen 4-verbonden driehoeken door alle 30.926 isomorfismeklassen op 16 hoekpunten te onderzoeken en alle 158.428 isomorfismeklassen op 17 hoekpunten. Berekening-tijd beperkingen betekende het beperken van zijn zoektocht naar monsters van 100.000 willekeurig gegenereerde niet-isomorfe triangulaties elk voor klassen op 18,19, en 20 hoekpunten. De uitgebreide zoekopdracht leverde 45 extra Kempe-vergrendelde triangulaties op, maar precies dezelfde resultaten als de oorspronkelijke zoekopdracht: elke Kempe-vergrendelde Rand in een triangulatie bevatte een bijbehorende Birkhoff-diamant.
waar vanaf hier? Tilley ‘ s uitgebreide zoekopdrachten bevestigden gemakkelijk dat de Birkhoff diamant een fundamentele Kempe-vergrendeling configuratie is. Hij heeft zijn vermoeden grondig getest, maar het blijft onbewezen. Als (of wanneer) Tilley ‘ s vermoeden waar is, dat wil zeggen dat de Birkhoff-diamant alleen de sleutel is tot 4 – kleurbaarheid, zou dat een verbazingwekkende vereenvoudiging van het probleem zijn: een enkele configuratie die het allemaal verklaart-wiskundige elegantie.

Het bewijs van het vermoeden van 4 kleuren vereist de inspanningen van vele vooraanstaande wiskundigen. Tilley ‘ s vermoeden dat de Birkhoff-diamant de enige fundamentele Kempe-vergrendelingsconfiguratie is, kan nog moeilijker te bewijzen zijn. Het experimentele bewijs is echter sterk. Theoretici zouden kunnen zeggen ‘ waarom de moeite?’Tilley’ s antwoord is dat onverzadigbare nieuwsgierigheid zal winnen: “immers, het vermoeden is gemakkelijk gesteld, begrijpelijk, en intrigerend, en biedt een overtuigende verklaring voor waarom alle vlakke grafieken zijn 4-kleurig.”
persoonlijke reactie
Wat was in eerste instantie de aanleiding voor uw enthousiasme voor het 4-kleurenprobleem en leidde u ertoe het zo intensief te bestuderen?het was mijn vaders obsessie met het probleem tijdens zijn pensionering en zijn wens om mij te gebruiken als klankbord voor zijn ideeën.
Wat zijn uw plannen voor toekomstig onderzoek op dit gebied?
Ik heb onlangs een ingewikkeld document besproken met een geheel andere benadering van het probleem met vier kleuren. Zoals de krant er nu uitziet, denk ik dat het gebreken heeft. Toch is het veelbelovend. Ik zou in de verleiding komen om een samenwerking te verkennen.
Leave a Reply