Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Inleiding
vierkantswortels worden meestal geschreven met behulp van een radicaal teken, zoals dit, ![]() . Maar er is een andere manier om het nemen van een wortel weer te geven. Je kunt rationele exponenten gebruiken in plaats van een radicaal. Een rationele exponent is een exponent die een fractie is. Bijvoorbeeld,
. Maar er is een andere manier om het nemen van een wortel weer te geven. Je kunt rationele exponenten gebruiken in plaats van een radicaal. Een rationele exponent is een exponent die een fractie is. Bijvoorbeeld, ![]() kan worden geschreven als
kan worden geschreven als ![]() .kan
.kan
zich niet voorstellen een getal te verhogen tot een rationele exponent? Ze zijn misschien moeilijk te wennen, maar rationele exponenten kunnen eigenlijk helpen sommige problemen te vereenvoudigen. Laten we de relatie onderzoeken tussen rationele (fractionele) exponenten en radicalen.
radicale expressies herschrijven met behulp van rationele exponenten
radicalen en fractionele exponenten zijn alternatieve manieren om hetzelfde uit te drukken. Je hebt al gezien hoe vierkantswortels kunnen worden uitgedrukt als een exponent aan de macht van de helft.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Denk eraan, door een getal te cuben stijgt het tot de macht van drie. Merk op dat in deze voorbeelden de noemer van de rationele exponent het getal 3 is.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and rationele exponenten: namelijk dat de nde wortel van een getal kan worden geschreven als ![]() of
of ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an expressie met een rationele exponent, je kunt het herschrijven met behulp van een radicaal. Zie in de bovenstaande tabel hoe de noemer van de rationale exponent de index van de wortel bepaalt. Dus, een exponent van ![]() vertaalt naar de vierkantswortel, een exponent van
vertaalt naar de vierkantswortel, een exponent van ![]() vertaalt naar de vijfde wortel of
vertaalt naar de vijfde wortel of ![]() , en
, en ![]() vertaalt naar de achtste wortel of
vertaalt naar de achtste wortel of ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
herschrijf de uitdrukking met de fractionele exponent als een radicaal. De noemer van de breuk bepaalt de wortel, in dit geval de kubuswortel. de haakjes in |
|
|
Antwoord |
|
|
Vergeet niet dat exponenten enkel te verwijzen naar de hoeveelheid onmiddellijk aan hun linkerkant, tenzij een scheidingsteken wordt gebruikt. Het voorbeeld hieronder lijkt erg op het vorige voorbeeld met één belangrijk verschil-Er zijn geen haakjes! Kijk wat er gebeurt.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. De noemer van de breuk bepaalt de wortel, in dit geval de kubuswortel. de exponent verwijst alleen naar het deel van de expressie direct links van de exponent, in dit geval x, maar niet de 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. In dit geval is de index van het radicaal 3, dus de rationele exponent is aangezien 4 buiten het radicaal valt, is het niet opgenomen in het groeps-symbool en verwijst de exponent er niet naar. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
Antwoord |
|
|
Rationale Exponenten met Tellers Andere dan Een
Alle tellers voor de fractiewaarde van de exponenten in de bovenstaande voorbeelden was 1. U kunt fractionele exponenten met andere tellers dan 1 gebruiken om wortels uit te drukken, zoals hieronder getoond. Zie je patronen in deze tabel?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
To herschrijf een radicaal met behulp van een fractionele exponent, de macht tot welke de radicand wordt verhoogd wordt de teller en de wortel wordt de noemer.
writing fractionele exponenten
elke radicaal in de vorm ![]() kan worden geschreven met behulp van een fractionele exponent in de vorm
kan worden geschreven met behulp van een fractionele exponent in de vorm ![]() .
.
de relatie tussen ![]() en
en ![]() werkt ook voor rationale exponenten met een teller van 1. Bijvoorbeeld, de radicale
werkt ook voor rationale exponenten met een teller van 1. Bijvoorbeeld, de radicale ![]() kan ook geschreven worden als
kan ook geschreven worden als ![]() , omdat elk getal dezelfde waarde blijft als het wordt verhoogd tot de eerste macht. U kunt nu zien waar de teller van 1 vandaan komt in de equivalente vorm van
, omdat elk getal dezelfde waarde blijft als het wordt verhoogd tot de eerste macht. U kunt nu zien waar de teller van 1 vandaan komt in de equivalente vorm van ![]() .
.
Simplifying Radical Expressions Using Rational Exponents and the Laws of Exponents
laten we nu enkele radicale expressies verkennen en zien hoe we ze kunnen vereenvoudigen. Hier is een radicale uitdrukking die vereenvoudigd moet worden, ![]() .
.
een methode om deze uitdrukking te vereenvoudigen is om groepen van a3 te factor en eruit te trekken, zoals hieronder in dit voorbeeld wordt getoond.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Antwoord |
|
|
U kunt ook een vereenvoudiging van deze expressie door na te denken over de radicale als een expressie met een rationale exponent, en met behulp van het principe dat een radicaal in de vorm ![]() kan worden geschreven met een gebroken exponent in de vorm
kan worden geschreven met een gebroken exponent in de vorm ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
beide vereenvoudigingsmethoden gaven hetzelfde resultaat, a2. Afhankelijk van de context van het probleem kan het makkelijker zijn om de ene of de andere methode te gebruiken, maar voor nu zul je merken dat je in staat was om deze expressie sneller te vereenvoudigen met behulp van rationele exponenten dan bij het gebruik van de “pull-out” methode.
laten we een ander voorbeeld proberen.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the rationele exponent terug naar radicale vorm. |
|
|
Antwoord |
|
|
Nogmaals, de alternatieve methode is om te werken aan de vereenvoudiging van onder de radicale door het gebruik van factoring. Voor het voorbeeld dat je net hebt opgelost, ziet het er zo uit.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
laten we een meer gecompliceerde uitdrukking proberen, ![]() . Deze uitdrukking heeft twee variabelen, een breuk en een radicaal. Laten we het stap voor stap doen en kijken of het gebruik van fractionele exponenten ons kan helpen het te vereenvoudigen.
. Deze uitdrukking heeft twee variabelen, een breuk en een radicaal. Laten we het stap voor stap doen en kijken of het gebruik van fractionele exponenten ons kan helpen het te vereenvoudigen.
laten we beginnen met het vereenvoudigen van de noemer, omdat dit is waar het radicale teken zich bevindt.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Een uitdrukking wordt gewoonlijk niet als vereenvoudigd beschouwd als zij een fractionele exponent of een radicaal in de noemer heeft. |
||
|
Antwoord |
|
||
Nou, dat duurde een tijdje, maar je deed het. Je paste toe wat je weet over fractionele exponenten, negatieve exponenten en de regels van exponenten om de expressie te vereenvoudigen.
samenvatting
een radicaal kan worden uitgedrukt als een uitdrukking met een fractionele exponent door de conventie te volgen ![]() . Het herschrijven van radicalen met fractionele exponenten kan nuttig zijn bij het vereenvoudigen van sommige radicale uitdrukkingen. Bij het werken met fractionele exponenten, onthoud dat fractionele exponenten zijn onderworpen aan alle van dezelfde regels als andere exponenten wanneer ze verschijnen in algebraïsche uitdrukkingen.
. Het herschrijven van radicalen met fractionele exponenten kan nuttig zijn bij het vereenvoudigen van sommige radicale uitdrukkingen. Bij het werken met fractionele exponenten, onthoud dat fractionele exponenten zijn onderworpen aan alle van dezelfde regels als andere exponenten wanneer ze verschijnen in algebraïsche uitdrukkingen.
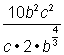
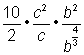
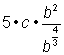
Leave a Reply