Lineaire regressieanalyse in Excel
de tutorial legt de basisprincipes van regressieanalyse uit en toont een paar verschillende manieren om lineaire regressie in Excel uit te voeren.
stel je dit voor: u krijgt een heleboel verschillende gegevens en wordt gevraagd om de verkoopcijfers van volgend jaar voor uw bedrijf te voorspellen. Je hebt tientallen, misschien zelfs honderden factoren ontdekt die de getallen kunnen beïnvloeden. Maar hoe weet je welke echt belangrijk zijn? Voer regressieanalyse uit in Excel. Het zal u een antwoord op deze en nog veel meer vragen te geven: Welke factoren zijn belangrijk en welke kunnen worden genegeerd? Hoe nauw zijn deze factoren met elkaar verbonden? En hoe zeker kun je zijn over de voorspellingen?
- regressieanalyse in Excel
- lineaire regressie in Excel met Analysetoolpak
- teken een lineaire regressiegrafiek
- regressieanalyse in Excel met formules
regressieanalyse in Excel – de basis
in statistische modellering wordt regressieanalyse gebruikt om de relaties tussen twee of meer variabelen te schatten:
afhankelijke variabele (aka criterion variable) is de belangrijkste factor die u probeert te begrijpen en te voorspellen.
onafhankelijke variabelen (ook wel verklarende variabelen of voorspellers genoemd) zijn de factoren die de afhankelijke variabele kunnen beïnvloeden.
regressieanalyse helpt u te begrijpen hoe de afhankelijke variabele verandert wanneer een van de onafhankelijke variabelen varieert en maakt het mogelijk om wiskundig te bepalen welke van deze variabelen echt een impact heeft.
technisch gezien is een regressieanalysemodel gebaseerd op de kwadratensom, wat een wiskundige manier is om de spreiding van datapunten te vinden. Het doel van een model is om de kleinst mogelijke kwadratensom te krijgen en een lijn te tekenen die het dichtst bij de gegevens komt.
in statistieken wordt onderscheid gemaakt tussen een enkelvoudige en meervoudige lineaire regressie. Eenvoudige lineaire regressie modelleert de relatie tussen een afhankelijke variabele en een onafhankelijke variabelen met behulp van een lineaire functie. Als je twee of meer verklarende variabelen gebruikt om de afhankelijke variabele te voorspellen, heb je te maken met meerdere lineaire regressie. Als de afhankelijke variabele wordt gemodelleerd als een niet-lineaire functie omdat de datarelaties geen rechte lijn volgen, gebruik dan niet-lineaire regressie. De focus van deze tutorial zal zijn op een eenvoudige lineaire regressie.
als voorbeeld nemen we de verkoopcijfers voor paraplu ‘ s van de laatste 24 maanden en kijken we naar de gemiddelde maandelijkse neerslag voor dezelfde periode. Teken deze informatie op een grafiek, en de regressielijn zal de relatie aantonen tussen de onafhankelijke variabele (regenval) en afhankelijke variabele (umbrella sales):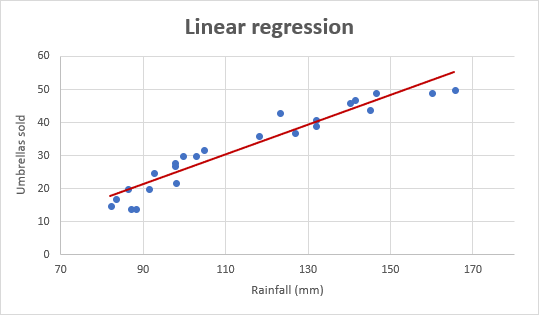
Lineaire regressievergelijking
wiskundig wordt een lineaire regressie gedefinieerd door deze vergelijking:
waarbij:
- x is een onafhankelijke variabele.
- y is een afhankelijke variabele.
- a is de Y-as, de verwachte gemiddelde waarde van y wanneer alle x-variabelen gelijk zijn aan 0. In een regressiegrafiek is het het punt waar de lijn de Y-as kruist.
- b is de helling van een regressielijn, de veranderingssnelheid voor y als x-veranderingen.
- ε is de willekeurige foutterm, die het verschil is tussen de werkelijke waarde van een afhankelijke variabele en de voorspelde waarde ervan.
De lineaire regressievergelijking heeft altijd een foutterm omdat voorspellers in het echte leven nooit perfect nauwkeurig zijn. Echter, sommige programma ‘ s, waaronder Excel, doen de fout term berekening achter de schermen. Dus, in Excel, doe je lineaire regressie met behulp van de kleinste kwadraten methode en zoek je coëfficiënten a en b zodanig dat:
in ons voorbeeld neemt de lineaire regressievergelijking de volgende vorm aan:
Umbrellas sold = b * rainfall + a
Er bestaan een handvol verschillende manieren om a en B te vinden. de drie belangrijkste methoden om lineaire regressieanalyse in Excel uit te voeren zijn:
- Regressietool meegeleverd met Analysis ToolPak
- spreidingsdiagram met een trendlijn
- Lineaire regressieformule
hieronder vindt u de gedetailleerde instructies voor het gebruik van elke methode.
lineaire regressie in Excel uitvoeren met Analysis ToolPak
dit voorbeeld laat zien hoe regressie in Excel wordt uitgevoerd met behulp van een speciaal gereedschap dat is meegeleverd met de Analysis ToolPak add-in.
Schakel de invoegtoepassing Analysis ToolPak in
Analysis ToolPak is beschikbaar in alle versies van Excel 2019 tot 2003, maar is standaard niet ingeschakeld. Zo, je nodig hebt om het handmatig in te schakelen. Hier is hoe:
- klik in uw Excel op Bestand > opties.
- in het dialoogvenster Excel-opties selecteert u invoegtoepassingen in de linkerzijbalk, controleer of Excel-invoegtoepassingen zijn geselecteerd in het vak beheren en klik op gaan.
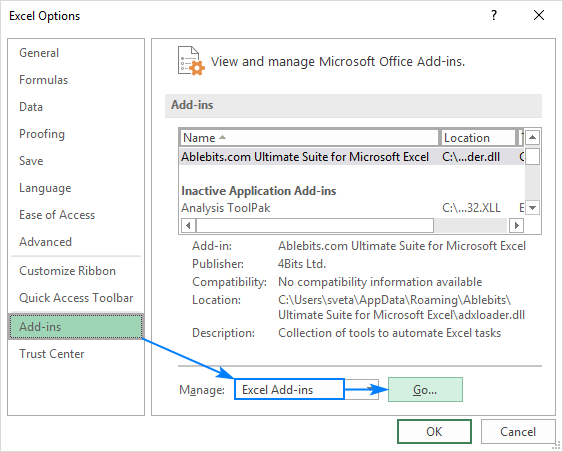
- in het dialoogvenster Invoegtoepassingen vinkt u Analysis Toolpak aan en klikt u op OK:
Dit zal de hulpmiddelen voor gegevensanalyse toevoegen aan het tabblad Gegevens van uw Excel-lint.
voer regressieanalyse uit
In dit voorbeeld gaan we een eenvoudige lineaire regressie doen in Excel. Wat we hebben is een lijst van de gemiddelde maandelijkse neerslag van de laatste 24 maanden in kolom B, dat is onze onafhankelijke variabele (voorspeller), en het aantal paraplu ‘ s verkocht in kolom C, dat is de afhankelijke variabele. Natuurlijk zijn er veel andere factoren die de verkoop kunnen beïnvloeden, maar voor nu richten we ons alleen op deze twee variabelen: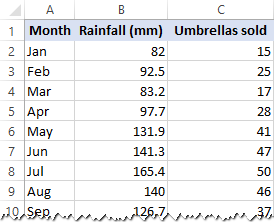
Met Analysis Toolpak toegevoegd ingeschakeld, voert u deze stappen uit om regressieanalyse uit te voeren in Excel:
- op het tabblad Data, in de analysegroep, klik op de knop Data-analyse.
- Selecteer regressie en klik op OK.
- configureer in het dialoogvenster regressie de volgende instellingen:
- Selecteer het invoerbereik Y, dat uw afhankelijke variabele is. In ons geval is het Paraplu verkoop (C1: C25).
- Selecteer het invoerbereik X, dat wil zeggen uw onafhankelijke variabele. In dit voorbeeld is het de gemiddelde maandelijkse neerslag (B1: B25).
Als u een meervoudig regressiemodel bouwt, selecteert u twee of meer aangrenzende kolommen met verschillende onafhankelijke variabelen.
- Vink het vak Labels aan als er headers aan de bovenkant van uw X-en Y-bereiken staan.
- kies de gewenste uitvoeroptie, een nieuw werkblad in ons geval.
- selecteer optioneel het selectievakje reststoffen om het verschil te krijgen tussen de voorspelde en de werkelijke waarden.
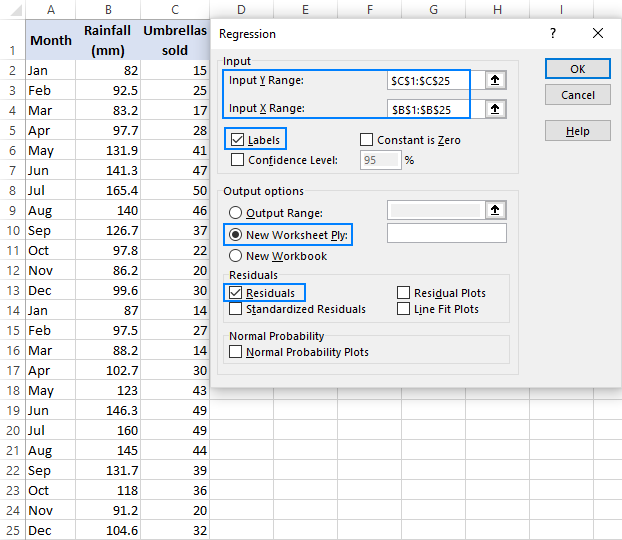
- klik op OK en observeer de uitvoer van de regressieanalyse die door Excel is gemaakt.
interpreteer de uitvoer van de regressieanalyse
zoals u zojuist hebt gezien, is het uitvoeren van regressie in Excel eenvoudig omdat alle berekeningen automatisch worden voorgevormd. De interpretatie van de resultaten is een beetje lastiger omdat je moet weten wat er achter elk nummer. Hieronder vindt u een uitsplitsing van 4 belangrijke delen van de regressieanalyse output.
regressieanalyse output: samenvatting Output
dit deel vertelt u hoe goed de berekende lineaire regressievergelijking past bij uw brongegevens.
Dit is wat elk stuk informatie betekent:
Multiple R. Het is de correlatiecoëfficiënt die de sterkte van een lineaire relatie tussen twee variabelen meet. De correlatiecoëfficiënt kan elke waarde tussen -1 en 1 zijn, en de absolute waarde geeft de relatiesterkte aan. Hoe groter de absolute waarde, hoe sterker de relatie:
- 1 betekent een sterke positieve relatie
- -1 betekent een sterke negatieve relatie
- 0 betekent helemaal geen relatie
R vierkant. Het is de determinatiecoëfficiënt, die wordt gebruikt als een indicator van de goedheid van fit. Het laat zien hoeveel punten vallen op de regressielijn. De R2-waarde wordt berekend uit de totale kwadratensom, meer precies, het is de som van de kwadraatafwijkingen van de oorspronkelijke gegevens van het gemiddelde.
in ons voorbeeld is R2 0,91 (afgerond naar 2 cijfers), wat fairy goed is. Dat betekent dat 91% van onze waarden passen in het regressieanalysemodel. Met andere woorden, 91% van de afhankelijke variabelen (y-waarden) worden verklaard door de onafhankelijke variabelen (x-waarden). Over het algemeen wordt R kwadraat van 95% of meer als een goede pasvorm beschouwd.
aangepast R-vierkant. Het is het R-vierkant aangepast voor het aantal onafhankelijke variabele in het model. U wilt deze waarde gebruiken in plaats van het R-kwadraat voor meerdere regressieanalyses.
standaardfout. Het is een andere goodness-of-fit maat die de precisie van uw regressieanalyse toont – hoe kleiner het getal, hoe zekerder u kunt zijn over uw regressievergelijking. Terwijl R2 het percentage van de variantie van de afhankelijke variabelen vertegenwoordigt dat door het model wordt verklaard, is de standaardfout een absolute maat die de gemiddelde afstand aangeeft dat de gegevenspunten van de regressielijn vallen.
waarnemingen. Het is gewoon het aantal waarnemingen in uw model.
regressieanalyse output: ANOVA
het tweede deel van de output is variantieanalyse (ANOVA):
In Principe splitst het de kwadratensom op in afzonderlijke componenten die informatie geven over de variabiliteitsniveaus binnen uw regressiemodel:
- df is het aantal vrijheidsgraden geassocieerd met de bronnen van variantie.
- SS is de kwadratensom. Hoe kleiner de resterende SS in vergelijking met de totale SS, hoe beter uw model past bij de gegevens.
- MS is het gemiddelde kwadraat.
- F is de F-statistiek, of F-test voor de nulhypothese. Het wordt gebruikt om de algemene betekenis van het model te testen.
- significantie F is de P-waarde van F.
het ANOVA-deel wordt zelden gebruikt voor een eenvoudige lineaire regressieanalyse in Excel, maar u moet zeker de laatste component van dichtbij bekijken. De significantie F waarde geeft een idee van hoe betrouwbaar (statistisch significant) uw resultaten zijn. Als de significantie F kleiner is dan 0,05 (5%), is uw model OK. Als het groter is dan 0,05, kunt u waarschijnlijk beter een andere onafhankelijke variabele kiezen.
regressieanalyse output: coëfficiënten
Deze sectie geeft specifieke informatie over de componenten van uw analyse:
De meest bruikbare component in deze sectie zijn coëfficiënten. Het stelt u in staat om een lineaire regressievergelijking in Excel te bouwen:
voor onze dataset, waarin y het aantal verkochte paraplu ’s is en x een gemiddelde maandelijkse regenval is, gaat onze Lineaire regressieformule als volgt:
Y = Rainfall Coefficient * x + Intercept
uitgerust met A-en b-waarden afgerond tot op drie decimalen, wordt het:
Y=0.45*x-19.074
bijvoorbeeld, met een gemiddelde maandelijkse regenval gelijk aan 82 mm, zou de parapluverkoop ongeveer 17,8 zijn:
0.45*82-19.074=17.8
op een vergelijkbare manier kunt u achterhalen hoeveel paraplu ‘ s zullen worden verkocht met elke andere maandelijkse regenval (x variabele) die u opgeeft.
regressieanalyse output: reststoffen
als u het Geschatte en werkelijke aantal verkochte paraplu ‘ s vergelijkt dat overeenkomt met de maandelijkse neerslag van 82 mm, zult u zien dat deze aantallen enigszins verschillen:
- geschatte: 17.8 (hierboven berekend)
- feitelijk: 15 (rij 2 van de brongegevens)
Waarom is het verschil? Omdat onafhankelijke variabelen nooit perfecte voorspellers zijn van de afhankelijke variabelen. En de reststoffen kunnen u helpen begrijpen hoe ver de werkelijke waarden verwijderd zijn van de voorspelde waarden:
Hoe maak je een lineaire regressiegrafiek in Excel
als je snel de relatie tussen de twee variabelen wilt visualiseren, teken dan een lineaire regressiegrafiek. Dat is heel makkelijk! Hier is hoe:
- Selecteer de twee kolommen met uw gegevens, inclusief headers.
- op het tabblad Invoegen, in de Chats-Groep, klik op het pictogram voor het spreidingsdiagram en selecteer de scatterminiatuur (de eerste):
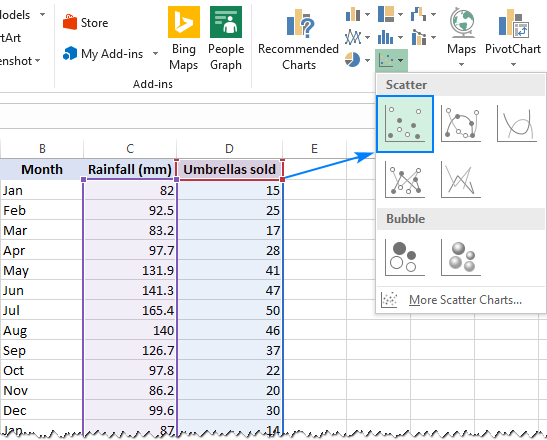
Dit zal een scatterplot in uw werkblad invoegen, die op deze lijkt:
- teken de regressielijn voor de kleinste kwadraten. Klik met de rechtermuisknop op een willekeurig punt en kies Trendline toevoegen… uit het contextmenu.
- in het rechterdeelvenster selecteert u de lineaire trendlijnvorm en vinkt u optioneel de Weergavevergelijking op het diagram aan om uw regressieformule te krijgen:
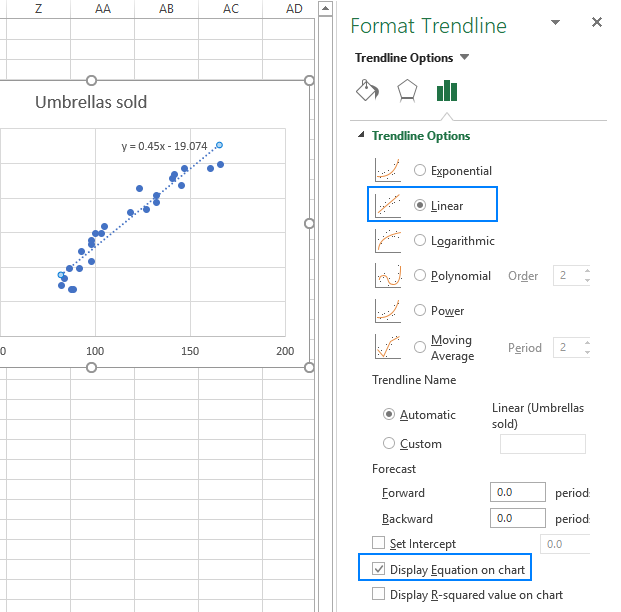
zoals u misschien merkt, is de regressievergelijking die Excel voor ons heeft gemaakt dezelfde als de lineaire regressieformule die we hebben gebouwd op basis van de Uitvoercoëfficiënten.
- Schakel naar de vulling & regeltabblad en pas de regel aan naar uw wens. U kunt bijvoorbeeld een andere lijnkleur kiezen en een vaste lijn gebruiken in plaats van een gestippelde lijn (selecteer een vaste lijn in het dashboard Type box):
Op dit punt ziet uw grafiek er al uit als een fatsoenlijke regressiegrafiek:
toch wilt u nog een paar verbeteringen aanbrengen:
- sleep de vergelijking waar u wilt.
- voeg AST-titels toe (knop grafiekelementen> AST-titels).
- als uw gegevenspunten in het midden van de horizontale en/of verticale as beginnen, zoals in dit voorbeeld, wilt u misschien de overmatige witruimte verwijderen. De volgende tip legt uit hoe dit te doen: schalen van de grafiek assen om witruimte te verminderen.
en zo ziet onze verbeterde regressiegrafiek eruit:
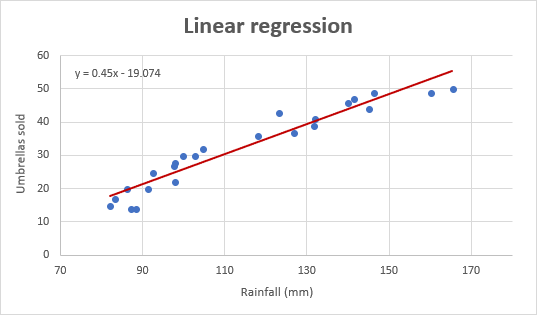belangrijke opmerking! In de regressiegrafiek moet de onafhankelijke variabele altijd op de X-as staan en de afhankelijke variabele op de Y-as. Als uw grafiek in omgekeerde volgorde is uitgezet, verwisselt u de kolommen in uw werkblad en tekent u het diagram opnieuw. Als het u niet is toegestaan om de brongegevens te herschikken, kunt u de x-en Y-assen rechtstreeks in een grafiek schakelen.
regressie in Excel met behulp van formules
Microsoft Excel heeft een paar statistische functies die u kunnen helpen bij het uitvoeren van lineaire regressieanalyse, zoals LINEST, SLOPE, INTERCPET en CORREL.
De functie LINEST gebruikt de least squares regressiemethode om een rechte lijn te berekenen die het beste de relatie tussen uw variabelen verklaart en een array geeft die die lijn beschrijft. U kunt de gedetailleerde uitleg van de syntaxis van de functie vinden in deze tutorial. Laten we nu gewoon een formule maken voor onze voorbeelddataset:
=LINEST(C2:C25, B2:B25)
omdat de LINEST-functie een reeks waarden retourneert, moet u deze invoeren als een matrixformule. Selecteer twee aangrenzende cellen in dezelfde rij, E2:F2 typ in ons geval de formule en druk op Ctrl + Shift + Enter om het te voltooien.
De formule geeft de B-coëfficiënt (E1) en de A-constante (F1) terug voor de reeds bekende lineaire regressievergelijking:
y = bx + a
Als u matrixformules in uw werkbladen niet gebruikt, kunt u A en b afzonderlijk berekenen met reguliere formules:
haal de y-intercept (a):
=INTERCEPT(C2:C25, B2:B25)
haal de helling (B):
=SLOPE(C2:C25, B2:B25)
Bovendien kunt u de correlatiecoëfficiënt (meerdere R in de samenvatting van de regressieanalyse) vinden die aangeeft hoe sterk de twee variabelen aan elkaar gerelateerd zijn:
=CORREL(B2:B25,C2:C25)
De volgende Schermafbeelding toont al deze Excel-regressieformules in actie:
zo doe je lineaire regressie in Excel. Dat gezegd hebbende, houd er rekening mee dat Microsoft Excel is geen statistisch programma. Als u nodig hebt om regressie-analyse uit te voeren op het professionele niveau, wilt u misschien gerichte software zoals XLSTAT, RegressIt, enz.
beschikbare downloads:
om onze Lineaire regressieformules en andere technieken die in deze tutorial worden besproken nader te bekijken, bent u van harte welkom om onze voorbeeldregressieanalyse in Excel-werkmap te downloaden.
- oplosser gebruiken in Excel met voorbeelden
- samengestelde rente berekenen in Excel
- CAGR (samengestelde jaarlijkse groei) berekenen in Excel
Leave a Reply