de grafiek van een lineaire ongelijkheid in een variabele is een getallenlijn. Gebruik een open cirkel voor < en > en een gesloten cirkel voor ≤ en ≥.

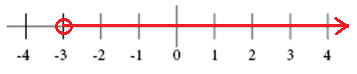
de grafiek voor x > -3

de grafiek voor x ≥ 2

ongelijkheden die dezelfde oplossing hebben worden equivalent genoemd. Er zijn eigenschappen van ongelijkheid en er waren eigenschappen van gelijkheid. Alle onderstaande eigenschappen gelden ook voor ongelijkheden met ≥ en ≤.

De opteleigenschap van ongelijkheid zegt dat het toevoegen van hetzelfde getal aan elke zijde van de ongelijkheid een gelijkwaardige ongelijkheid oplevert

$$If \: x>y,\: dan\: x+z>y+z$$

$$If\: x<y,\: dan\: x+z<y+z$$

de eigenschap aftrekken van ongelijkheid vertelt ons dat het aftrekken van hetzelfde getal aan beide zijden van een ongelijkheid een gelijkwaardige ongelijkheid geeft.

$$If \: x>y,\: then\: X-z>y-z$$

$$If\: x<y,\: then\: x-z<y-z$$

de vermenigvuldiging eigenschap van ongelijkheid vertelt ons dat vermenigvuldiging aan beide zijden van een ongelijkheid met een positief getal een gelijkwaardige ongelijkheid produceert.

$ $ If\: x> y \: en\: z>0,\: dan\: xz>yz$$

$$Als\: x<y\: en\: z>0,\: dan\: xz<yz$$

Vermenigvuldiging in elke zijde van een ongelijkheid met een negatief getal aan de andere kant resulteert niet in een gelijkwaardige ongelijkheid, tenzij we ook omkeren van de richting van de ongelijkheid symbool

$$Als \: x>y \: en\: z<0,\: dan\: xz<yz$$

$$Als\: x<y\: en\: z<0,\: dan\: xz>yz$$

hetzelfde geldt voor de deling eigenschap van ongelijkheid.

verdeling van beide zijden van een ongelijkheid met een positief getal leidt tot een gelijkwaardige ongelijkheid.

$$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x<y\: en\: z>0,\: dan\: \ frac{x}{z}<\frac{y}{z}$$

en deling aan beide zijden van een ongelijkheid met een negatief getal geeft een gelijkwaardige ongelijkheid als het ongelijkheidssymbool omgekeerd is.

$$Als \: x>y \: en\: z<0,\: dan\: \frac{x}{z}<\frac{y} / {z}$$

$$Als\: x<y\: en\: z<0,\: dan\: \frac{x}{z}>\frac{y} / {z}$$

Om het oplossen van een multi-stap ongelijkheid u doen als u wist bij het oplossen van multi-stap vergelijkingen. Neem één ding op het moment bij voorkeur te beginnen met het isoleren van de variabele van de constanten. Bij het oplossen van multi-stap ongelijkheden is het belangrijk om niet te vergeten om het ongelijkheid teken te keren bij het vermenigvuldigen of delen met negatieve getallen.

voorbeeld

los de ongelijkheid op

$$-2\left (x + 3 \ right )<10$$