Fibonacci-reeks
De Fibonacci-reeks is de getallenreeks:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
het volgende getal wordt gevonden door de twee getallen ervoor op te tellen:
- de 2 wordt gevonden door de twee getallen ervoor op te tellen (1+1),
- de 3 wordt gevonden door de twee getallen ervoor op te tellen (1+2),
- de 5 is (2+3),
- enzovoort!
voorbeeld: het volgende getal in de bovenstaande reeks is 21+34 = 55
zo eenvoudig is het!
Hier is een langere lijst:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
kunt u de volgende getallen achterhalen?
maakt een spiraal
wanneer we vierkanten maken met deze breedtes, krijgen we een mooie spiraal:
zie je hoe de vierkanten netjes bij elkaar passen?
bijvoorbeeld 5 en 8 maken 13, 8 en 13 maken 21, enzovoort.

deze spiraal wordt gevonden in de natuur!
zie: Natuur,de gulden snede en Fibonacci
de regel
De Fibonacci-reeks kan als een “regel” worden geschreven (zie sequenties en reeksen).
eerst worden de termen genummerd vanaf 0 zoals dit:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
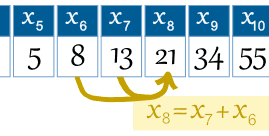
dus term nummer 6 wordt x6 genoemd (wat gelijk is aan 8).
|
Voorbeeld: de 8e termijn is x8 = x7 + x6 |
 |
Dus kunnen we schrijven de regel:
De Regel is xn = xn−1 + xn−2
waar:
- xn is de term getal “n”
- xn−1 is de vorige zittingsperiode (n−1)
- xn−2 is de term voor dat (n−2)
Voorbeeld: blok 9 wordt berekend, zoals dit:
Golden Ratio
En hier is een verrassing. Wanneer we twee opeenvolgende Fibonacci-getallen nemen, is hun verhouding zeer dicht bij de gulden snede “φ” die ongeveer 1,618034 is…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
We hoeven niet te beginnen met 2 en 3, hier koos ik willekeurig 192 en 16 (en kreeg de reeks 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
Het duurt langer om goede waarden te krijgen, maar het toont aan dat niet alleen de Fibonacci-reeks Dit kan doen!
met behulp van de gulden snede om Fibonacci − getallen te berekenen
en nog verrassender is dat we elk Fibonacci−getal kunnen berekenen met behulp van de gulden snede:
xn = φn – (1-φ)n√5
het antwoord komt uit als een geheel getal, precies gelijk aan de optelling van de twee voorgaande termen.
voorbeeld: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
toen ik hiervoor een rekenmachine gebruikte (alleen de gulden snede tot 6 decimalen invoeren) kreeg ik het antwoord 8.00000033 , een nauwkeurigere berekening zou dichter bij 8 liggen.
probeer n=12 en zie wat je krijgt.
u kunt ook een Fibonacci-getal berekenen door het vorige Fibonacci-getal te vermenigvuldigen met de gulden snede en vervolgens af te ronden (werkt voor getallen boven 1):
Voorbeeld: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (afgerond)
enkele interessante dingen
Hier is de Fibonacci-reeks weer:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Er is een interessant patroon:
- Kijk naar het getal x3 = 2. Elk 3e getal is een veelvoud van 2 (2, 8, 34, 144, 610, …)
- Kijk naar het getal x4 = 3. Elk 4e getal is een veelvoud van 3 (3, 21, 144,…)
- Kijk naar het getal x5 = 5. Elk 5e getal is een veelvoud van 5 (5, 55, 610,…)
enzovoort (elk n-de getal is een veelvoud van xn).
1/89 = 0,011235955056179775…
merk op dat de eerste paar cijfers (0,1,1,2,3,5) de Fibonacci-reeks zijn?
op een manier die ze allemaal zijn, behalve meerdere getallen (13, 21, enz.) overlappen, zoals dit:
… etc …
0,011235955056179775… = 1/89
termen onder nul
De reeks werkt ook onder nul, als volgt:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(bewijs jezelf dat elk getal wordt gevonden door de twee getallen ervoor op te tellen!)
in feite heeft de reeks onder nul dezelfde getallen als de reeks boven nul, behalve dat ze een + – + – volgen … patroon. Het kan als volgt geschreven worden:
x – n =(-1)n+1 xn
Wat zegt dat term − – n “gelijk is aan (-1)n+1 keer term “n”, en de waarde (-1)n+1 maakt netjes de juiste +1, -1, +1, -1, … patroon.
geschiedenis
Fibonacci was niet de eerste die op de hoogte was van de sequentie, het was honderden jaren eerder in India bekend!

over Fibonacci de Man
zijn echte naam was Leonardo Pisano Bogollo, en hij woonde tussen 1170 en 1250 in Italië.”Fibonacci “was zijn bijnaam, wat grofweg”zoon van Bonacci” betekent.
hij was niet alleen beroemd om de Fibonacci-reeks, hij hielp ook Hindoe-Arabische cijfers te verspreiden (zoals onze huidige getallen). 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) door Europa in plaats van Romeinse cijfers (I, II, III, IV, V, enz.). Dat heeft ons allemaal een hoop problemen bespaard! Dank je Leonardo.

Fibonacci Day
Fibonacci Day is 23 November, omdat het de cijfers” 1, 1, 2, 3 ” heeft die deel uitmaken van de reeks. Dus volgende Nov 23 laat het iedereen weten!


Leave a Reply