equivalente fracties

equivalente fracties vertegenwoordigen hetzelfde deel van een geheel

de beste manier om over gelijkwaardige breuken na te denken is dat het fracties zijn die dezelfde totale waarde hebben.

bijvoorbeeld, als we een taart precies in het midden snijden, in twee stukken van gelijke grootte, is één stuk hetzelfde als de helft van de taart.

en als een andere taart (dezelfde grootte) in 4 gelijke stukken wordt gesneden, dan vertegenwoordigen twee stukken van die taart dezelfde hoeveelheid taart als 1/2.

dus we kunnen zeggen dat 1/2 gelijk is aan 2/4.

laat gelijkwaardige breuken u niet verwarren!

kijk eens naar de vier cirkels hierboven.Kun je zien dat de ene “1/2″, de twee” 1/4 “en de vier” 1/8 ” nemen dezelfde hoeveelheid gebied gekleurd in Oranje voor hun cirkel?Nou dat betekent dat elk gebied gekleurd in Oranje is een gelijkwaardige fractie of gelijke hoeveelheid. Daarom kunnen we zeggen dat 1/2 gelijk is aan 2/4, en 1/2 is ook gelijk aan 4/8. En ja Sprinkhaan, 2/4 is een gelijkwaardige fractie voor 4/8 too.As je weet al dat we gek zijn op regels. Dus, laten we eens kijken naar de regel om te controleren of twee breuken gelijk of gelijk zijn. De regel voor gelijkwaardige breuken kan een beetje moeilijk uit te leggen zijn, maar hou vol, we zullen de dingen in slechts een beetje ophelderen.

Hier is de Regel

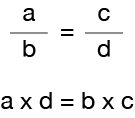
Wat zegt deze Regel is dat twee breuken gelijkwaardig zijn (gelijk) alleen als het product van de teller (a) van de eerste fractie en de noemer (d) van de andere breuk is gelijk aan het product van de noemer (b) van de eerste breuk, en de teller (c) van de andere fractie.

een product betekent simpelweg dat je vermenigvuldigt.

dat klinkt als een mondvol, dus laten we het proberen met getallen…

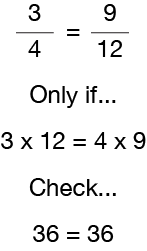
Test de regel

nu stoppen we de getallen in de regel voor gelijkwaardige fracties om er zeker van te zijn dat je het “koud”hebt. 3/4 is alleen gelijk aan 9/12 als het product van de teller (3) van de eerste fractie en de noemer (12) van de andere fractie gelijk is aan het product van de noemer (4) van de eerste fractie en de teller (9) van de andere fractie. Dus we weten dat 3/4 gelijk is aan 9/12, omdat 3×12 = 36 en 4×9 = 36. Een eenvoudige manier om te kijken hoe te controleren op gelijkwaardige breuken is om te doen wat wordt genoemd “cross-vermenigvuldig”, wat betekent veelvoud van de teller van een breuk met de noemer van de andere breuk. Doe dan hetzelfde in omgekeerde richting. Vergelijk nu de twee antwoorden om te zien of ze gelijk zijn. Als ze gelijk zijn, dan zijn de twee fracties gelijkwaardige fracties.

de grafiek hieronder laat zien hoe je vermenigvuldigt…

OK, laten we er een doen met getallen waarbij de breuken niet equivalent zijn…

zoals je kunt zien in dit voorbeeld, is 1/2 geen equivalente fractie van 2/3.

Als u eraan denkt de cross-vermenigvuldigingsmethode te gebruiken, zou u geen problemen moeten hebben met het verifiëren van gelijkwaardige breuken.

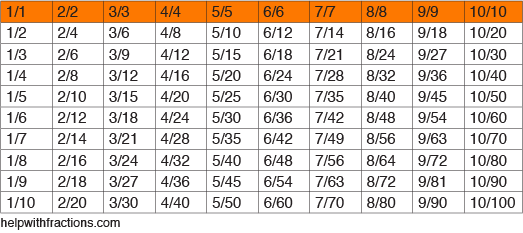
onderstaande tabel geeft een overzicht van enkele veel voorkomende breuken en hun equivalenten. Lees de tafel van links naar rechts. Wat het je laat zien zijn waarden vermenigvuldigd met verschillende variaties van breuken gelijk aan “1”. Weet je nog dat elk getal gedeeld door zichzelf gelijk is aan “1” toch?