Ik heb altijd “permutatie” en “combinatie” verward-welke is welke?

Hier is een eenvoudige manier om te onthouden: permutatie klinkt ingewikkeld, nietwaar? En dat is het ook. Met permutaties is elk klein detail belangrijk. Alice, Bob en Charlie is anders dan Charlie, Bob en Alice (Vul hier de namen van je vrienden in).

combinaties, aan de andere kant, zijn vrij eenvoudig. De details doen er niet toe. Alice, Bob en Charlie is hetzelfde als Charlie, Bob en Alice.

permutaties zijn voor lijsten (volgorde is belangrijk) en combinaties zijn voor groepen (volgorde doet er niet toe).

een ” combinatieslot “zou eigenlijk een”permutatieslot” moeten worden genoemd. De volgorde waarin je de nummers plaatst is belangrijk.

Een waar “combinatieslot” zou zowel 10-17-23 als 23-17-10 als correct accepteren.

permutaties: de harige details

laten we beginnen met permutaties, of alle mogelijke manieren om iets te doen. We gebruiken de chique term “permutatie”, dus we gaan ons bekommeren om elk detail, inclusief de volgorde van elk item. Laten we zeggen dat we 8 personen hebben:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

op hoeveel manieren kunnen we een prijs van de 1e, 2e en 3e plaats toekennen onder acht deelnemers? (Gold / Silver / Bronze)

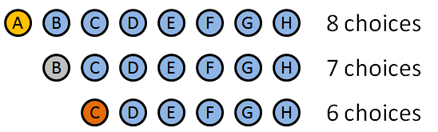
We gaan permutaties gebruiken omdat de volgorde waarin we deze medailles uitdelen van belang is. Hier is hoe het opgesplitst:

• gouden medaille: 8 keuzes: A B C D E F G H (slim hoe ik de namen liet overeenkomen met letters, eh?). Stel dat A Het goud wint.
• zilveren medaille: 7 keuzes: B C D E F G H. laten we zeggen dat B het zilver wint.
• bronzen medaille: 6 keuzes: C D E F G H. laten we zeggen… C wint het brons.

We kozen bepaalde mensen om te winnen, maar de details doen er niet toe: we hadden eerst 8 keuzes, dan 7, dan 6. Het totale aantal opties was $8 * 7 * 6 = 336$.

laten we eens kijken naar de details. We moesten 3 van de 8 mensen bestellen. Om dit te doen, begonnen we met alle opties (8) en namen ze een voor een weg (7, dan 6) totdat we geen medailles meer hadden.

we weten dat de faculteit:

helaas doet dat te veel! We willen alleen $8 * 7 * 6$. Hoe kunnen we de faculteit om vijf uur ‘stoppen’?

Dit is waar permutaties cool worden: Merk op hoe we er vanaf willen komen $5 * 4 * 3 * 2 * 1$. Wat is een andere naam hiervoor? 5 faculteit!

dus, als we doen 8!/5! we krijgen:

en waarom hebben we het getal 5 gebruikt? Omdat het overbleef nadat we 3 medailles uit 8 hadden geplukt. Een betere manier om dit te schrijven is:

waarbij 8!/(8-3)! is gewoon een mooie manier om te zeggen ” Gebruik de eerste 3 nummers van 8!”. Als we n items totaal hebben en k in een bepaalde volgorde willen kiezen, krijgen we:

en dit is de fancy permutatie formule: u hebt N items en wilt het aantal manieren vinden waarop k items kunnen worden geordend:

combinaties, Ho!

combinaties zijn eenvoudig. Orde doet er niet toe. Je kunt het mengen en het ziet er hetzelfde uit. Laten we zeggen dat ik een vrek ben en geen aparte gouden, zilveren en bronzen medailles kan betalen. Ik kan me alleen lege blikken veroorloven.

op hoeveel manieren kan ik 3 blikjes aan 8 personen geven?

in dit geval doet de volgorde die we mensen kiezen er niet toe. Als ik een blik geef aan Alice, Bob en dan Charlie, is het hetzelfde als aan Charlie, Alice en dan Bob geven. Hoe dan ook, ze zijn net zo teleurgesteld.

Dit roept een interessant punt op — we hebben hier enkele redundanties. Alice Bob Charlie = Charlie Bob Alice. Laten we even uitzoeken op hoeveel manieren we 3 mensen kunnen herschikken.

Nou, we hebben 3 keuzes voor de eerste persoon, 2 voor de tweede, en slechts 1 voor de laatste. Dus we hebben $3 * 2 * 1 $ Manieren om opnieuw te regelen 3 personen.

wacht even … dit lijkt een beetje op een permutatie! Je hebt me erin geluisd.

Dat heb ik inderdaad gedaan. Als je N mensen hebt en je wilt weten hoeveel arrangementen er voor allemaal zijn, dan is het gewoon n faculteit of N!

dus, als we 3 blikjes hebben om weg te geven, zijn er 3! of 6 variaties voor elke keuze die we kiezen. Als we willen uitzoeken hoeveel combinaties we hebben, creëren we alle permutaties en delen we door alle redundanties. In ons geval krijgen we 336 permutaties (van boven), en we delen door de 6 redundanties voor elke permutatie en krijgen 336/6 = 56.

de algemene formule is

wat betekent ” Zoek alle manieren om k mensen uit n te kiezen, en deel door de k! variant”. Als we dit opschrijven, krijgen we onze combinatieformule, of het aantal manieren om K-items te combineren uit een verzameling van n:

soms wordt C (n, k) geschreven als:

wat de binomiale coëfficiënt is.

een paar voorbeelden

Hier zijn een paar voorbeelden van combinaties (orde doet er niet toe) van permutaties (orde doet er toe).

• combinatie: een team van 3 personen kiezen uit een groep van 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

  permutatie: het kiezen van een President, VP en Waterboy uit een groep van 10. $ P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

• Combinatie: 3 desserts kiezen uit een menu van 10. C (10,3) = 120.

  permutatie: een lijst van uw 3 favoriete desserts, in volgorde, uit een menu van 10. P (10,3) = 720.

onthoud de formules niet, begrijp waarom ze werken. Combinaties klinken eenvoudiger dan permutaties, en dat zijn ze. Je hebt minder combinaties dan permutaties.

andere berichten in deze serie

1. eenvoudige permutaties en combinaties
2. navigeren door een raster met behulp van combinaties en permutaties
3. Hoe combinaties te begrijpen met behulp van vermenigvuldiging
4. waarom vermenigvuldigen we combinaties?