Definitieve integralen
u wilt misschien eerst Introduction to Integration lezen!
integratie
|
integratie kan worden gebruikt om gebieden, volumes, centrale punten en vele nuttige dingen te vinden. Maar het wordt vaak gebruikt om het gebied onder de grafiek van een functie als deze te vinden: |
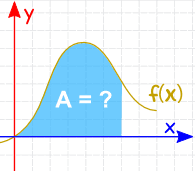 |
|
|
het gebied kan worden gevonden door slices toe te voegen die nul benaderen in de breedte: en er zijn Integratieregels die ons helpen het antwoord te krijgen. |
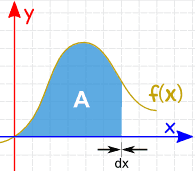 |
Notatie
Het symbool voor “Integraal” is een stijlvolle “S” (voor de “Som”, het idee van tellen plakjes):
Na afloop van het Integraal Symbool zetten we de functie we willen de integraal van (de Integrand).
en eindig dan met dx om te betekenen dat de plakjes in de x-richting gaan (en in de breedte nul benaderen).
Bepaalde Integraal
een bepaalde integraal heeft begin-en eindwaarden: met andere woorden, er is een interval .
a en b (genaamd grenzen, grenzen of grenzen) worden aan de onder-en bovenkant van de “S” gezet, zoals dit:
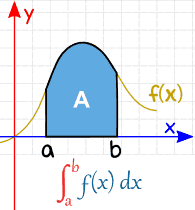 |
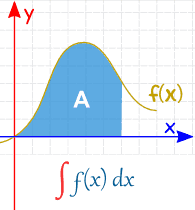 |
|
| Definite Integral (from a to b) |
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
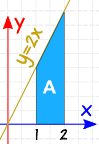
voorbeeld: Wat is 2 2 1 2x dx
We worden gevraagd om de definitieve integraal, van 1 tot 2, van 2x dx
eerst moeten we de onbepaalde integraal vinden.
met behulp van de regels van integratie vinden we dat ∫2x dx = x2 + C
nu berekenen dat op 1, en 2:
- bij x = 1: ∫2x dx = 12 + C
- bij x = 2: ∫2x dx = 22 + C
Aftrekken:
en “C” wordt geschrapt … dus met een Bepaalde Integralen kunnen we negeren C.
Resultaat:

Controleren: met een eenvoudige vorm, laten we ook proberen de berekening van het gebied door de geometrie:
Een = 2+42 × 1 = 3
Ja, het heeft een oppervlakte van 3.
(Yay!)
notatie: Kunnen We laten zien dat de onbepaalde integraal (zonder +C) binnen vierkante haken, met de grenzen a en b na, zoals:
Voorbeeld (vervolg)
Een goede manier om te laten zien uw antwoord:
=
Laten we een ander voorbeeld:
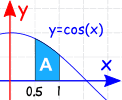
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
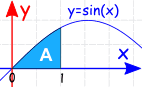
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
De onbepaalde integraal is: ∫sin(x) dx = −cos(x) + C
aangezien we gaan van 0, kunnen we gewoon berekenen de integraal op x=1?
−cos (1) = -0,540…
Wat? Is het negatief? Maar het ziet er positief uit in de grafiek.
Well … we hebben een fout gemaakt!
omdat we de integraal bij x=0 moeten aftrekken. We moeten niet aannemen dat het nul is.
dus laten we het goed doen, de een van de ander Aftrekken:
=
dat is beter!
maar we kunnen negatieve gebieden hebben als de kromme onder de as ligt:
voorbeeld:
De definitieve integraal, van 1 tot 3, van cos(x) dx:
merk op dat een deel ervan positief is, en een ander negatief.
De definitieve integraal zal de nettowaarde berekenen.
laten we de berekeningen doen:
=
Jump er is meer negatief dan positief met het nettoresultaat van -0.700….
dus we hebben dit belangrijke ding om te onthouden:
integreer cos(x) met verschillende begin-en eindwaarden om zelf te zien hoe positieven en negatieven werken.
positieve oppervlakte
maar soms willen we dat alle oppervlakte als positief wordt behandeld (zonder dat het deel onder de as wordt afgetrokken).
in dat geval moeten we de gebieden afzonderlijk berekenen, zoals in dit voorbeeld:

voorbeeld: Wat is de totale oppervlakte tussen y = cos (x) en de x-as, van x = 1 tot x = 3?
Dit is zoals het voorbeeld dat we net deden, maar nu verwachten we dat alle oppervlakte positief is (stel je voor dat we het moesten schilderen).
we hebben nu Dus te maken met de onderdelen afzonderlijk:
- Één voor het gebied boven de x-as
- Één voor de oppervlakte onder de x-as
De curve kruist de x-as bij x = π/2, dus we hebben:
Van 1 tot π/2:
= sin(π/2) − sin(1)
Van π/2 tot 3:
= sin(3) − sin(π/2)
die laatste komt negatief uit, maar we willen dat het positief is, dus:
totale oppervlakte = 0,159… + 0.859… = 1.018…
Dit is heel anders dan het antwoord in het vorige voorbeeld.
continu
Oh ja, de functie die we integreren moet continu zijn tussen a en b: geen gaten, sprongen of verticale asymptoten (waarbij de functie omhoog/omlaag gaat naar oneindigheid).
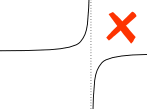
voorbeeld:
een verticale asymptoot tussen a en b beïnvloedt de definitieve integraal.
eigenschappen
gebied boven − gebied onder
De integraal voegt het gebied boven de as toe maar trekt het gebied Hieronder af, voor een “nettowaarde”:
functies toevoegen
De integraal van f+g is gelijk aan de integraal van f plus de integraal van G:
Omkeren van het interval
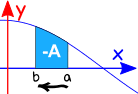
het Omkeren van de richting van het interval geeft het negatieve van de oorspronkelijke richting.
![]()


Leave a Reply