De mooiste en belangrijkste wiskundige vergelijkingen
wiskunde is meer een marathon dan een sprint — het is een lange, langzame en gestage grind, met zeldzame momenten van doorbraak. Toch, af en toe, krijgen we die gewaardeerde “Eureka” momenten, die korte regels van letters en cijfers die de wetenschap voor altijd veranderen. Hier zijn enkele van de beroemdste vergelijkingen, van de oude Grieken tot de moderne natuurkunde.
stelling van Pythagora (530 v. Chr.)
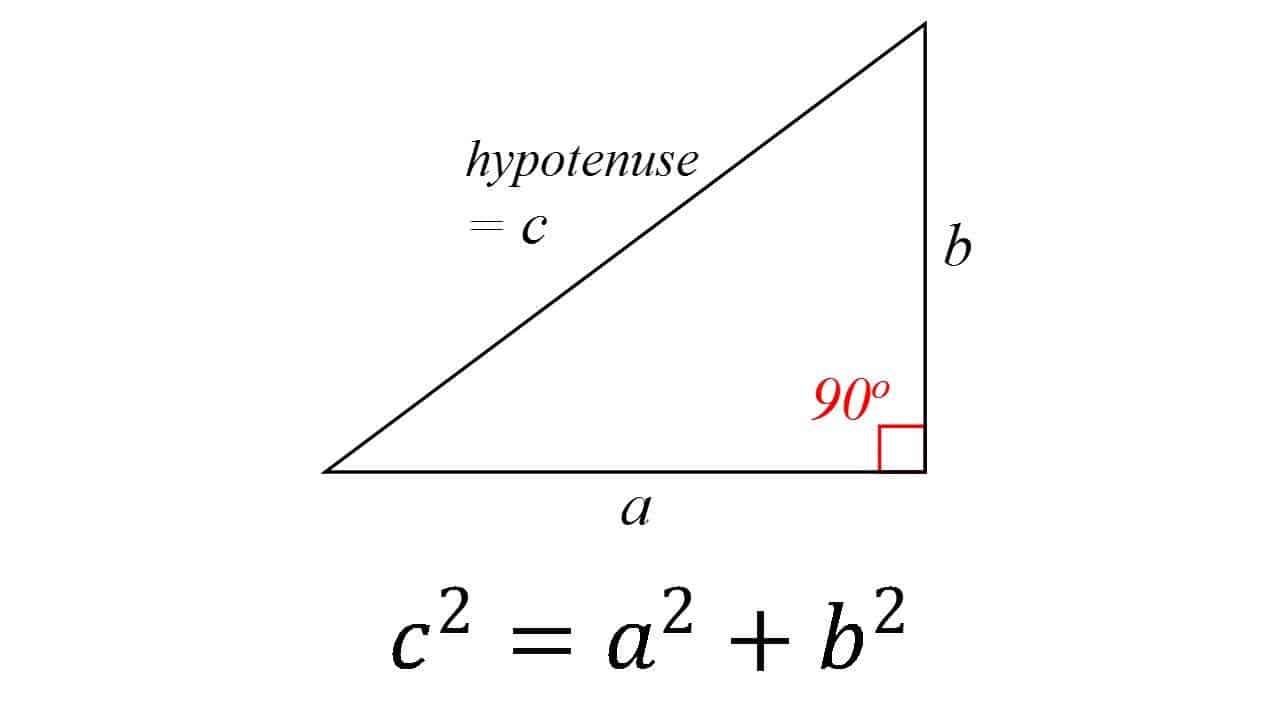
Dit is een van de pijlers van de gehele meetkunde: in een rechthoekige driehoek is het vierkant van de hypotenusa (de zijde tegenover de rechte hoek) gelijk aan de som van de kwadraten van de andere twee. De theorie wordt over het algemeen toegeschreven aan de Griekse wiskundige Pythagoras, hoewel er enig bewijs is dat Babylonische wiskundigen de formule begrepen. Het is ook heel goed mogelijk dat de stelling bekend was bij veel mensen, maar hij was de eerste om het te bewijzen.
de stelling heeft vele bewijzen gekregen-mogelijk het meest voor elke wiskundige stelling. Ze zijn zeer divers, met inbegrip van zowel meetkundige bewijzen en algebraïsche bewijzen, waarvan sommige dateren duizenden jaren terug.
complexe getallen

De Italiaanse wiskundige Gerolamo Cardano is de eerste die complexe getallen heeft geïntroduceerd en ze destijds “fictief” noemde. De wiskundige ontwikkeling van “i” als het imaginaire getal dat de vierkantswortel van -1 vertegenwoordigt wordt echter toegeschreven aan Leonhard Euler, een van de belangrijkste wiskundigen en wetenschappers in de menselijke geschiedenis.
complexe getallen zijn in principe getallen die niet echt bestaan, maar die zeer nuttig zijn voor een aantal berekeningen. Ze bestaan uit getallen met een reëel deel (de getallen die we allemaal kennen) en een imaginair deel (het ik hier vertegenwoordigd) en hebben praktische toepassingen op vele gebieden, waaronder natuurkunde, scheikunde, biologie, Economie, Elektrotechniek en statistiek.
de logaritmen

logaritmen zijn in principe de inverse functie van exponentiatie. Je hebt een getal (N) nodig, een basis (a), en de logaritme van N in basis a zal x zijn, waar N gelijk is aan a tot de macht van x. het lijkt misschien slechts een andere manier om hetzelfde te schrijven (en in zekere zin is het dat), maar logaritmen hebben een groot aantal praktische toepassingen, die worden gebruikt in de psychologie, economie, en metingen van vele fysische fenomenen (zoals pH of aardbeving magnitude).
logaritmen werden publiekelijk voorgesteld door John Napier in 1614, in een boek getiteld Mirifici Logaritmorum Canonis Descriptio (Description of the Wonderful Rule of Logaritms) — een passende titel. Een speciaal geval van logaritme is de natuurlijke logaritme-e, waar e een irrationeel en transcendentaal getal is dat ongeveer gelijk is aan 2.71828182845. E zelf heeft een fascinerende geschiedenis en een indrukwekkend aantal toepassingen, maar dat is een verhaal voor een andere keer.
Calculus
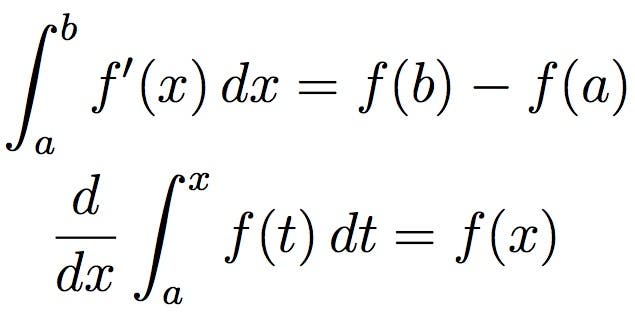
weinig deelgebieden van de wiskunde zijn zo impactvol geweest als de calculus. Calculus werd in de 17e eeuw ontwikkeld door Isaac Newton en Gottfried Wilhelm Leibniz en wordt veel gebruikt in de wetenschap, techniek en economie. Calculus richt zich meestal op het omgaan met kleine hoeveelheden, in het bijzonder oneindig kleine hoeveelheden. Door middel van calculus kunnen deze als reële getallen worden behandeld, ook al zijn ze technisch oneindig klein.
voor een eenvoudigere visualisatie kan integratie, zoals hierboven afgebeeld, worden gezien als het meten van het gebied onder een curve, gedefinieerd door een functie.
de Zwaartekrachtswet
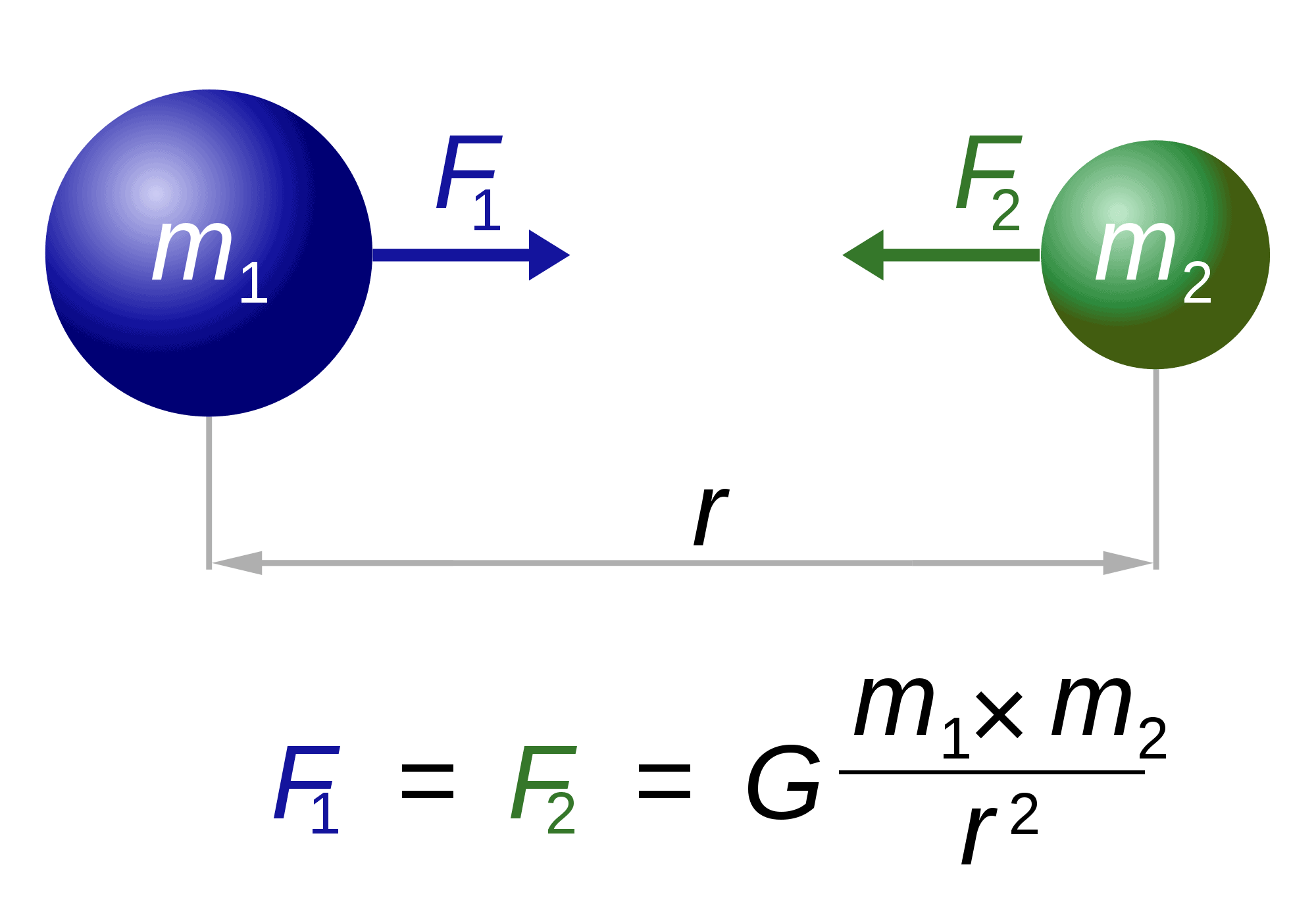
Over Newton gesproken, Hij is ook “verantwoordelijk” voor een van de beroemdste en meest spectaculaire vergelijkingen ter wereld: de zwaartekrachtswet.
de wet beschrijft in principe hoe twee lichamen van massa ‘ s m1 en m2 tot elkaar worden aangetrokken. De kracht (F1, F2) is omgekeerd evenredig met het kwadraat van de afstand tussen hen (r). De enige overgebleven factor, G, is een gravitatieconstante. De aard van deze constante blijft ongrijpbaar.
algemene relativiteit

gedurende bijna 200 jaar definieerde de wet van Newton ons niveau van begrip van mechanica. Einstein ‘ s werk in de 20e eeuw tilde dingen naar een hoger niveau — deze twee prestaties torenen op de hoogste sokkels in de wereld van de natuurkunde.
De algemene relativiteitstheorie is in wezen een meetkundige theorie van de zwaartekracht, die de theorie van Newton generaliseert en een Verenigde beschrijving geeft van de zwaartekracht als een meetkundige eigenschap van ruimte en tijd — of ruimtetijd. In het bijzonder toonde Einstein niet alleen aan dat er zoiets bestaat als “ruimtetijd” die de drie dimensies samenvoegt met de 4e dimensie van de tijd, maar hij toonde ook aan dat deze ruimtetijd kan worden gekromd door zwaartekracht, waarbij de kromming direct gerelateerd is aan de energie en het momentum van welke materie en straling dan ook aanwezig is.
tweede wet van de thermodynamica
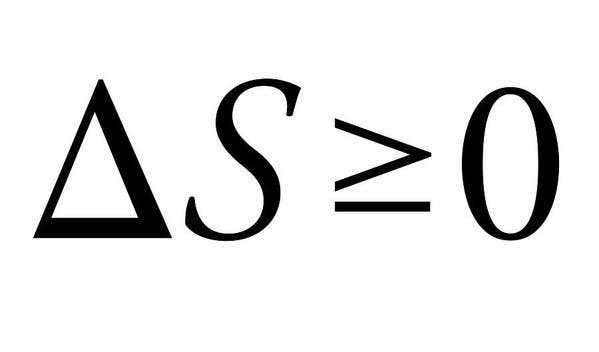
De Tweede Wet van de thermodynamica is de reden waarom we geen mooie dingen in het universum kunnen hebben. De vier wetten van de thermodynamica bepalen fundamentele fysische grootheden (temperatuur, energie en entropie) die thermodynamische systemen karakteriseren. De tweede, in het bijzonder, valt hier op door zijn eenvoud, maar absoluut enorme implicaties.
de wet stelt in wezen dat de som van de entropieën van de interagerende thermodynamische systemen altijd moet toenemen of hoogstens constant moet blijven. Wanneer energie verandert van de ene vorm naar de andere of materie beweegt rond, de entropie (of stoornis) in een gesloten systeem toeneemt. Alle verschillen in temperatuur, druk en dichtheid hebben de neiging om na een tijdje af te vlakken
Maxwell ‘ s vergelijkingen
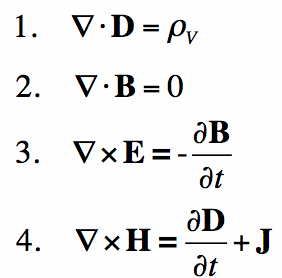
eenvoudig gezegd zijn Maxwell ’s vergelijkingen voor elektromagnetisme wat Newton’ s wet is voor mechanica. Ze bieden een wiskundige basis voor klassiek elektromagnetisme, klassieke optica en elektrische circuits. Ze worden veel gebruikt in het apparaat waar je dit op Leest-in principe alle elektronische apparaten.de wetten van Maxwell beschrijven hoe elektrische en magnetische velden worden gegenereerd door ladingen, stromen en veranderingen van de velden. Een belangrijke doorbraak was de demonstratie dat elektrische en magnetische velden zich voortplanten met de snelheid van het licht.
Euler ‘ s Identity

ten slotte is dit waarschijnlijk de meest elegante vergelijking, een ding van Opperste schoonheid, omdat het alle “basis” getallen omvat:
- 0, wat neutraal is voor optellen en aftrekken;
- 1, Wat neutraal is voor vermenigvuldiging en deling;
- e, wat het getal van Euler (zie boven), de basis van natuurlijke logaritmen;
- i is de imaginaire eenheid (zie boven); en
- π is pi, de verhouding tussen de omtrek van een cirkel en de diameter.
het vinden van een relatie die al deze getallen verenigt is adembenemend, en lijkt vrij onwaarschijnlijk. De demonstratie is niet echt eenvoudig, maar je kunt het hier zien.het is niet meer dan gepast dat professor Keith Devlin aan de Stanford universiteit de vergelijking beschreef en zei: “als een sonnet van Shakespeare dat de essentie van de liefde vastlegt, of een schilderij dat de schoonheid van de menselijke vorm naar voren brengt die veel meer is dan alleen maar huiddiep, reikt de vergelijking van Euler tot in de diepten van het bestaan”het is niet vaak dat wiskunde en natuurkunde neerkomen op eenvoudige en elegante vergelijkingen — maar als ze dat doen, is het nogal een aanblik om te aanschouwen.
Leave a Reply