Inleiding

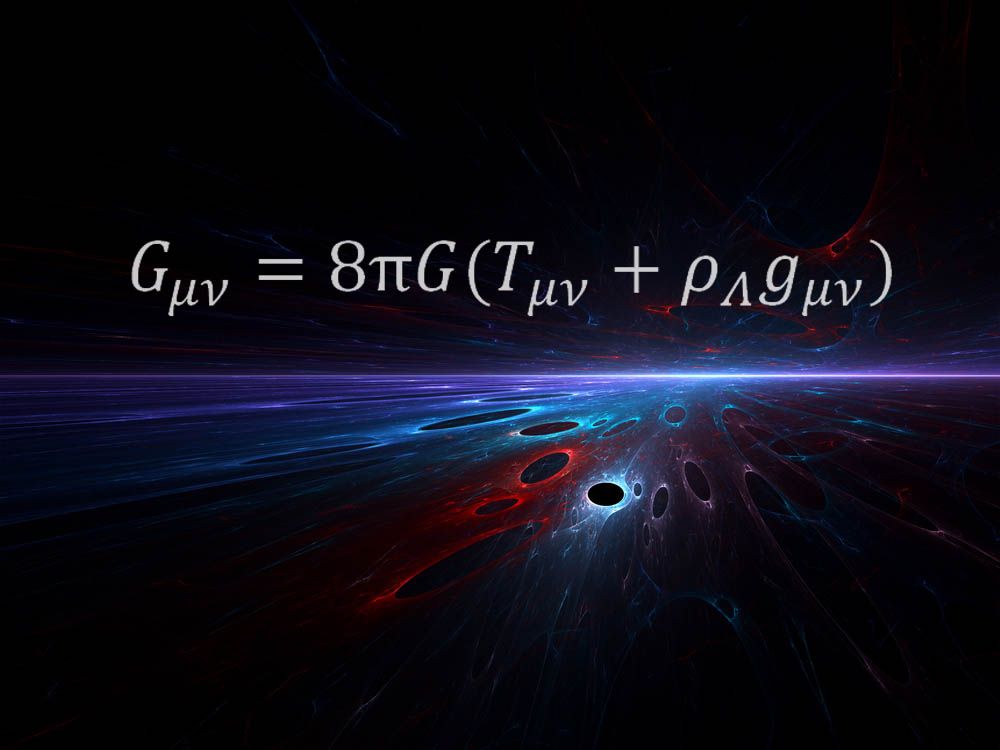
wiskundige vergelijkingen zijn niet alleen nuttig — veel zijn vrij prachtig. En veel wetenschappers geven toe dat ze vaak dol zijn op bepaalde formules, niet alleen vanwege hun functie, maar ook vanwege hun vorm, en de eenvoudige, poëtische waarheden die ze bevatten.hoewel sommige beroemde vergelijkingen, zoals Albert Einsteins E = mc^2, het grootste deel van de publieke glorie in handen hebben, hebben veel minder bekende formules hun kampioenen onder wetenschappers. LiveScience vroeg natuurkundigen, astronomen en wiskundigen voor hun favoriete vergelijkingen; hier is wat we gevonden hebben:

Algemene relativiteitstheorie

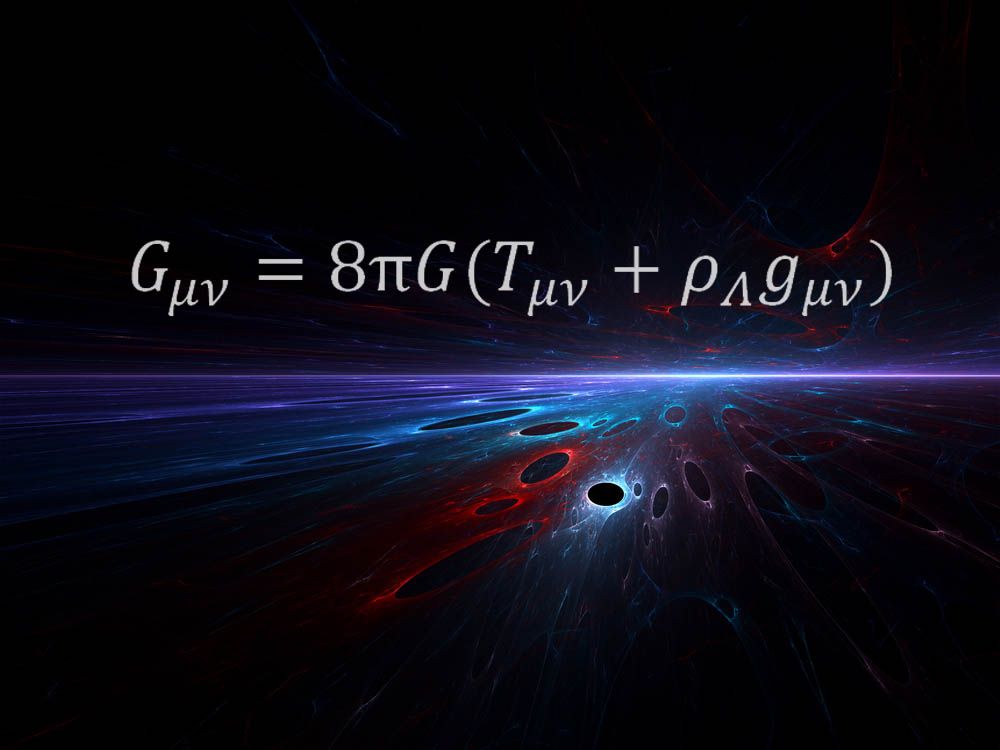
De vergelijking hierboven werd geformuleerd door Einstein als onderdeel van zijn baanbrekende algemene relativiteitstheorie in 1915. De theorie veranderde hoe wetenschappers zwaartekracht begrepen door de kracht te beschrijven als een kromming van het weefsel van ruimte en tijd.

“Het is nog steeds verbazingwekkend voor mij dat een dergelijke wiskundige vergelijking kan beschrijven wat ruimte-tijd is alles over,” zei Space Telescope Science Institute astrofysicus Mario Livio, die de vergelijking nomineerde als zijn favoriet. “Al Einstein’ s ware genie is belichaamd in deze vergelijking.”

” de rechterkant van deze vergelijking beschrijft de energie-inhoud van ons universum (inclusief de ‘donkere energie’ die de huidige kosmische versnelling voortstuwt), ” legde Livio uit. “De linkerkant beschrijft de geometrie van ruimte-tijd. De gelijkheid weerspiegelt het feit dat in Einsteins algemene relativiteit, massa en energie de meetkunde bepalen, en tegelijkertijd de kromming, wat een manifestatie is van wat we zwaartekracht noemen.”het is een zeer elegante vergelijking,” zei Kyle Cranmer, een natuurkundige aan de Universiteit van New York, eraan toevoegend dat de vergelijking de relatie tussen ruimte-tijd en materie en energie onthult. “Deze vergelijking vertelt u hoe ze zijn gerelateerd-hoe de aanwezigheid van de zon vervormt ruimte-tijd, zodat de aarde beweegt rond het in een baan, enz. Het vertelt je ook hoe het universum is geëvolueerd sinds de oerknal en voorspelt dat er zwarte gaten zouden moeten zijn.”

The Standard Model

een ander van de theorieën van de fysica, het standaardmodel beschrijft de verzameling van fundamentele deeltjes die momenteel verondersteld worden deel uit te maken van ons universum.de theorie kan worden samengevat in een hoofdvergelijking genaamd het standaardmodel Lagrangian (vernoemd naar de 18e-eeuwse Franse wiskundige en astronoom Joseph Louis Lagrange), die werd gekozen door theoretisch natuurkundige Lance Dixon van het SLAC National Accelerator Laboratory in Californië als zijn favoriete formule.

“Het heeft met succes alle elementaire deeltjes en krachten beschreven die we tot nu toe in het laboratorium hebben waargenomen — behalve de zwaartekracht,” vertelde Dixon aan LiveScience. “Dat omvat natuurlijk de recent ontdekte Higgs (zoals) boson, phi in de formule. Het is volledig zelf-consistent met kwantummechanica en speciale relativiteit.”

De standaard modeltheorie is echter nog niet verenigd met de algemene relativiteitstheorie, waardoor ze de zwaartekracht niet kan beschrijven.

Calculus

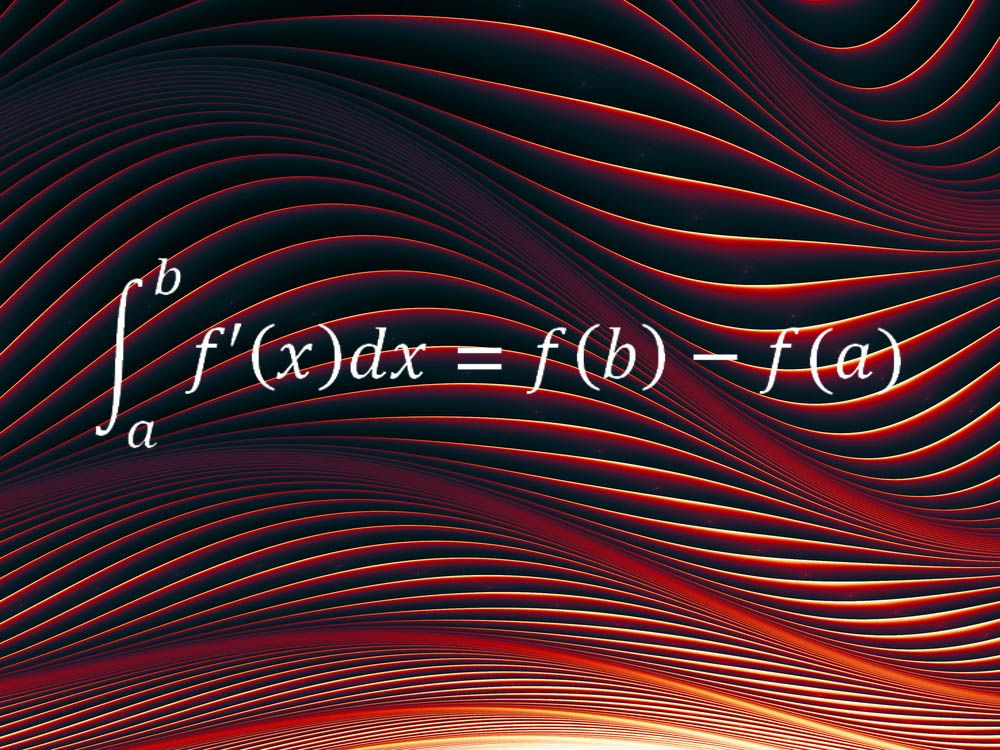
terwijl de eerste twee vergelijkingen specifieke aspecten van ons universum beschrijven, kan een andere favoriete vergelijking worden toegepast op allerlei situaties. De fundamentele stelling van calculus vormt de ruggengraat van de wiskundige methode die bekend staat als calculus, en verbindt zijn twee hoofdideeën, het concept van de integraal en het concept van de afgeleide.

” in eenvoudige woorden, zegt dat de netto verandering van een gladde en continue hoeveelheid, zoals een afgelegde afstand, over een bepaald tijdsinterval (d.w.z. het verschil in de waarden van de hoeveelheid aan het eind van het tijdsinterval) is gelijk aan de integraal van de snelheid van verandering van die hoeveelheid, dat wil zeggen de integraal van de snelheid,” zei Melkana Brakalova-Trevithick, voorzitter van de wiskunde-afdeling aan de Fordham University, die deze vergelijking koos als haar favoriet. “De fundamentele stelling van calculus (FTC) stelt ons in staat om de netto verandering over een interval te bepalen gebaseerd op de snelheid van verandering over het gehele interval.”

de zaden van calculus begonnen in de oudheid, maar veel ervan werd in de 17e eeuw samengesteld door Isaac Newton, die calculus gebruikte om de bewegingen van de planeten rond de zon te beschrijven.

stelling van Pythagoras

een” oude maar goede ” vergelijking is de beroemde stelling van Pythagoras, die elke beginnende meetkundestudent leert.

deze formule beschrijft hoe, voor een rechthoekige driehoek, het kwadraat van de lengte van de hypotenusa, c, (de langste zijde van een rechthoekige driehoek) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden (a en b). Dus a^2 + b^2 = c^2

“Het allereerste wiskundige feit dat me verbaasde was de stelling van Pythagoras,” zei wiskundige Daina Taimina van Cornell University. “Ik was toen een kind en het leek me zo geweldig dat het werkt in de meetkunde en het werkt met getallen!”

1 = 0,999999999….

Deze eenvoudige vergelijking, die stelt dat de hoeveelheid 0.999, gevolgd door een oneindige reeks van negen, is gelijk aan één, is de favoriet van wiskundige Steven Strogatz van Cornell University.

” Ik hou van hoe eenvoudig het is — iedereen begrijpt wat het zegt — maar hoe provocerend het is, ” zei Strogatz. “Veel mensen geloven niet dat het waar zou kunnen zijn. Het is ook prachtig gebalanceerd. De linkerkant vertegenwoordigt het begin van de wiskunde; de rechterkant vertegenwoordigt de mysteries van de oneindigheid.”

speciale relativiteit

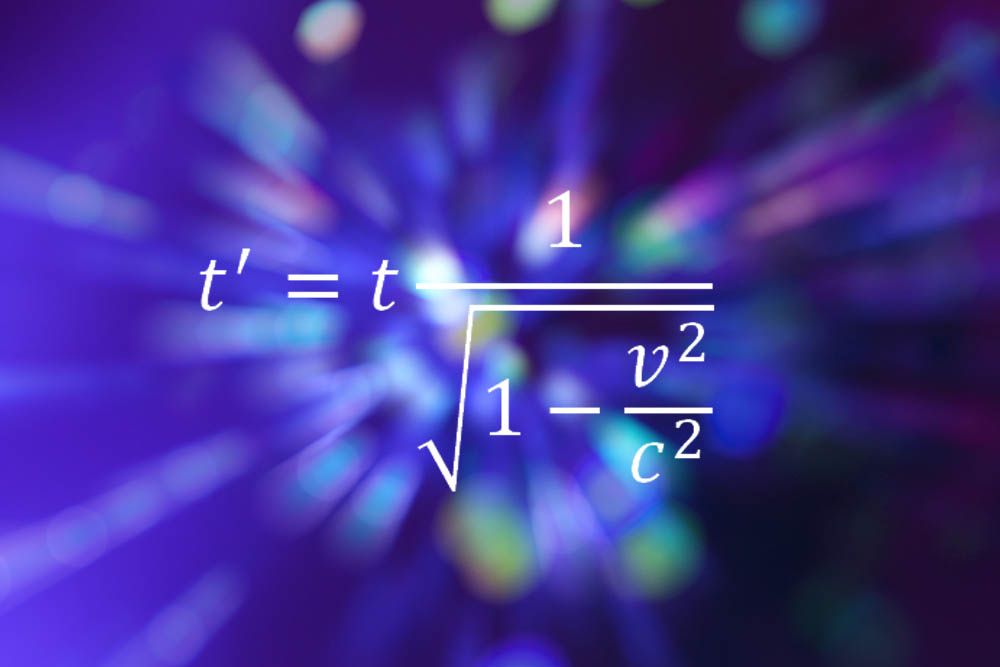
Einstein maakt de lijst opnieuw met zijn formules voor speciale relativiteit, die beschrijft hoe tijd en ruimte niet absoluut zijn concepten, maar eerder relatief afhankelijk van de snelheid van de waarnemer. De vergelijking hierboven laat zien hoe de tijd verwijdt, of vertraagt, hoe sneller een persoon beweegt in welke richting dan ook.”het punt is dat het echt heel eenvoudig is,” zei Bill Murray, een deeltjesfysicus in het CERN laboratorium in Genève. “Er is niets wat een A-niveau student niet kan doen, geen complexe derivaten en spooralgebra’ s. Maar wat het belichaamt is een hele nieuwe manier van kijken naar de wereld, een hele houding ten opzichte van de realiteit en onze relatie ermee. Plotseling wordt de starre onveranderlijke kosmos weggevaagd en vervangen door een persoonlijke wereld, gerelateerd aan wat je waarneemt. Je gaat van buiten het universum, naar beneden kijkend, naar een van de componenten erin. Maar de concepten en de wiskunde kunnen worden begrepen door iedereen die dat wil.Murray zei dat hij de voorkeur gaf aan de speciale relativiteitsvergelijkingen boven de meer gecompliceerde formules in Einsteins latere theorie. “Ik kon nooit de wiskunde van de algemene relativiteitstheorie volgen,” zei hij.

Euler ’s equation

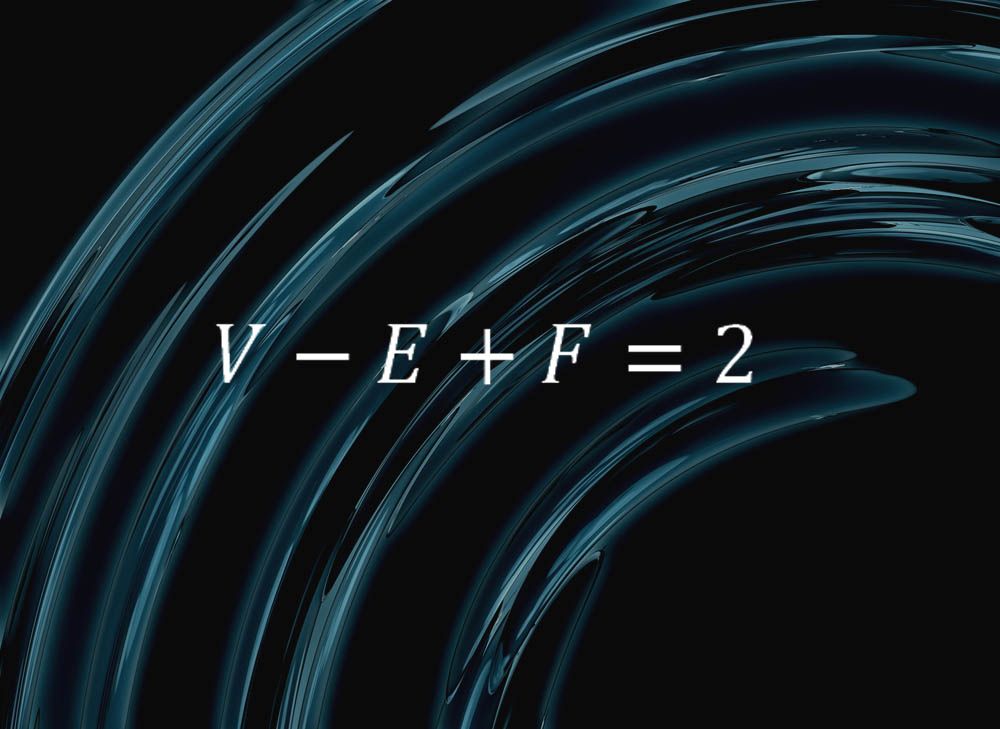
Deze eenvoudige formule vat iets zuivers samen over de aard van bollen:

” Het zegt dat als je het oppervlak van een bol opsnijdt in vlakken, randen en hoekpunten, en laat F Het aantal vlakken zijn, E het aantal randen en V het aantal hoekpunten, dan krijg je altijd V – E + F = 2,” zei Colin Adams, een wiskundige aan het Williams College in Massachusetts.

” neem bijvoorbeeld een tetraëder, bestaande uit vier driehoeken, zes randen en vier hoekpunten, ” legde Adams uit. “Als je hard in een tetraëder blies met flexibele vlakken, zou je het kunnen afronden tot een bol, dus in die zin kan een bol in vier vlakken, zes randen en vier hoekpunten worden gesneden. En we zien dat V-E + F = 2. Hetzelfde geldt voor een piramide met vijf gezichten-vier driehoekige, en een vierkant — acht randen en vijf hoekpunten,” en elke andere combinatie van gezichten, randen en hoekpunten.

“A very cool fact! De combinatoriek van de hoekpunten, randen en gezichten is het vastleggen van iets heel fundamenteels over de vorm van een bol,” Adams zei.

Euler-Lagrange-vergelijkingen en de stelling van Noether

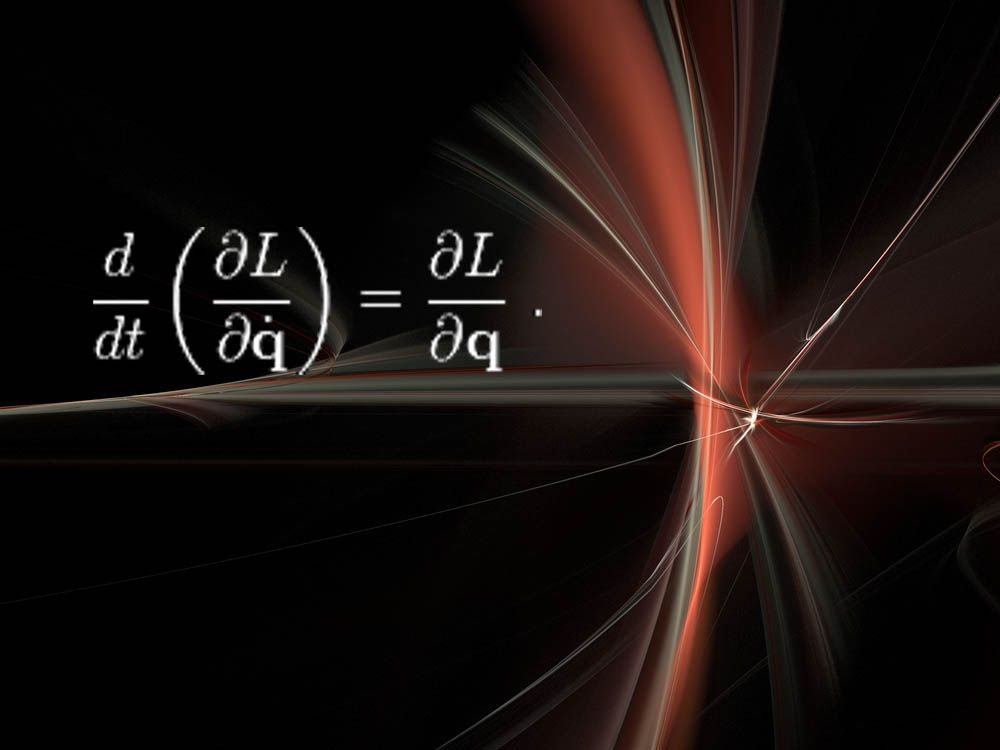
“Deze zijn vrij abstract, maar verbazingwekkend krachtig,” zei NYU ‘ s Cranmer. “Het leuke is dat deze manier van denken over de natuurkunde een aantal grote revoluties in de natuurkunde heeft overleefd, zoals kwantummechanica, relativiteit, enz.”

Hier staat L voor de Lagrangiaan, wat een maat is voor energie in een fysisch systeem, zoals veren, hefbomen of fundamentele deeltjes. “Het oplossen van deze vergelijking vertelt u hoe het systeem zal evolueren met de tijd,” Cranmer zei.

een spin-off van de Lagrangiaanse vergelijking wordt de stelling van Noether genoemd, naar de Duitse wiskundige Emmy Noether uit de 20e eeuw. “Deze stelling is echt fundamenteel voor de natuurkunde en de rol van symmetrie,” Cranmer zei. “Informeel, de stelling is dat als uw systeem een symmetrie heeft, dan is er een overeenkomstige wet behoud. Bijvoorbeeld, het idee dat de fundamentele wetten van de fysica vandaag dezelfde zijn als morgen (tijdsymmetrie) impliceert dat energie wordt behouden. Het idee dat de wetten van de fysica hier hetzelfde zijn als in de ruimte impliceert dat het momentum behouden blijft. Symmetrie is misschien het drijvende concept in de fundamentele fysica, voornamelijk als gevolg van de bijdrage.”

De Callan-Symanzik vergelijking

“De Callan-Symanzik vergelijking is een belangrijke eerste beginselen vergelijking van 1970, essentieel voor het beschrijven van hoe naïeve verwachtingen zal falen in een grote wereld,” zei theoretisch natuurkundige Matt Strassler van de Rutgers University.

de vergelijking heeft talrijke toepassingen, waaronder de mogelijkheid voor natuurkundigen om de massa en de grootte van het proton en het neutron te schatten, die de kernen van atomen vormen.

basisfysica vertelt ons dat de gravitatiekracht, en de elektrische kracht, tussen twee objecten proportioneel is aan de inverse van de afstand tussen hen in het kwadraat. Op een eenvoudig niveau geldt hetzelfde voor de sterke kernkracht die protonen en neutronen bindt om de kernen van atomen te vormen, en die quarks bindt om protonen en neutronen te vormen. Kleine kwantumfluctuaties kunnen echter de afhankelijkheid van een kracht van afstand enigszins veranderen, wat dramatische gevolgen heeft voor de sterke nucleaire kracht.

“Het voorkomt dat deze kracht afneemt op lange afstanden, en zorgt ervoor dat het quarks vangt en combineert om de protonen en neutronen van onze wereld te vormen,” zei Strassler. “Wat de Callan-Symanzik vergelijking doet is betrekking hebben op dit dramatische en moeilijk te berekenen effect, belangrijk wanneer is ongeveer de grootte van een proton, meer subtiele maar gemakkelijker te berekenen effecten die kunnen worden gemeten wanneer is veel kleiner dan een proton.”

the minimal surface equation

“De minimal surface equation codeert op de een of andere manier de mooie zeepfilms die zich op draad vormen grenzen als je ze in zeepwater dompelt,” zei wiskundige Frank Morgan van Williams College. “Het feit dat de vergelijking ‘niet-lineair’ is, waarbij machten en producten van derivaten betrokken zijn, is de gecodeerde wiskundige hint voor het verrassende gedrag van zeepfilms. Dit in tegenstelling tot meer bekende lineaire partiële differentiaalvergelijkingen, zoals de warmtevergelijking, de golfvergelijking en de Schrödingervergelijking van de kwantumfysica.”