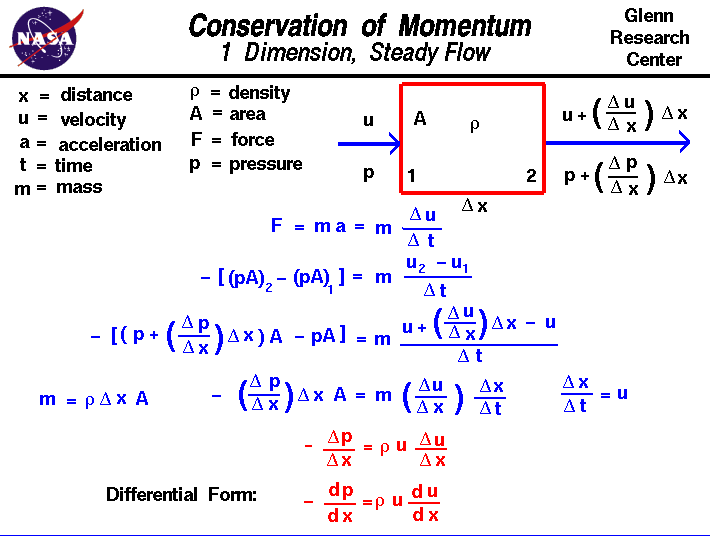
het behoud van momentum is een fundamenteel concept van fysicalong with theconservation of energy and theconservation of mass.Momentum wordt gedefinieerd als de massa van een object vermenigvuldigd met de snelheid van het object.Het behoud van momentum stelt dat, binnen een bepaald probleemgebied, de hoeveelheid momentum constant blijft;momentum wordt niet gecreëerd of vernietigd, maar alleen veranderd door de werking van krachten zoals beschreven in Newton ‘ s wetten van beweging.Het omgaan met momentum is moeilijker dan het omgaan met massa en energie omdat hetomentum een andere kwantiteit heeft die zowel een magnitude als een richting heeft. Het Momentum wordt in alle drie fysieke richtingen tegelijkertijd behouden. Het is nog moeilijker bij het omgaan met agas omdat krachten in de ene richting het momentum in een andere richting kunnen beà nvloeden vanwege de botsingen van veel moleculen.Op deze dia zullen we een zeer, zeer vereenvoudigd stroomprobleem presenteren waarbij eigenschappen slechts in één richting veranderen.Het probleem wordt verder vereenvoudigd door een gestage stroom te overwegen die niet verandert met de tijd en door de krachten te beperken tot die welke verband houden met thepressure.Be zich ervan bewust dat echte stroomproblemen veel complexer zijn dan dit simpele voorbeeld.

laten we eens kijken naar de stroom van een gas door een domein waarin de stroomeigenschappen slechts in één richting veranderen, die we “x”zullen noemen. Het gas komt het domein binnen in station 1 met een zekere snelheid u en een aantal drukpanden verlaat station 2 met een andere waarde van snelheid en druk. Voor de eenvoud gaan we ervan uit dat de dichtheid r constant blijft binnen het domein en dat het gebied A waar het gas doorheen stroomt ook constant blijft. De locatie van stations 1 en 2 worden gescheiden door een afstand genaamd del x. (Delta is de kleine driehoek op de slide en is de Griekse letter “d”. Wiskundigen gebruiken dit symbool vaak om een verandering of variatie van een grootheid aan te duiden. Het lettertype web print ondersteunt de Griekse letters niet, dus we zullen het gewoon “del”noemen.) Een verandering met afstand wordt aangeduid als een gradiëntom verwarring te voorkomen met een verandering met de tijd die wordt genoemd een snelheid.De snelheidsgradiënt wordt aangegeven door del u / del x;de verandering in snelheid perchange in afstand. Dus bij station 2 wordt de snelheid gegeven door de snelheid van 1 plus de gradiënt maal de afstand.

een soortgelijke uitdrukking geeft de druk op de uitgang:

Newton ‘ s tweede wet van beweging stelt dat kracht F gelijk is aan de verandering in momentum met betrekking tot de tijd. Voor een object met constant massm reduceert dit tot de massa maal versnelling a.An acceleratie is een verandering in snelheid met een verandering in de tijd(del u / del t). Vervolgens:

De kracht in dit probleem komt voort uit de drukgradiënt. Aangezien druk een kracht per oppervlakte-eenheid is, is de netto kracht op ons vloeistofdomein de druk keer het gebied bij de uitgang minus de druk keer het gebied bij de ingang.

het minteken aan het begin van deze uitdrukking wordt gebruikt omdat gassen zich verplaatsen van een gebied met hoge druk naar een gebied met lage druk; als de druk met X toeneemt, zal de snelheid afnemen. Onze uitdrukkingen vervangen voor velocity en pressure:

vereenvoudig:

op te Merken dat (del x / del t) is thevelocity en dat de massa is de dichtheid r maal het volume (gebied maal del x):

Vereenvoudig:

De del-p / del x en del u / del xrepresent de druk en snelheid verlopen.Als we ons domein verkleinen tot differentiële groottes, worden deze gradiënten differentiëlen:

Dit is een eendimensionale, stabiele vorm van Euler ‘ s Equation.It het is interessant op te merken dat de drukval van een vloeistof (de term links) evenredig is met zowel de waarde van de snelheid als de gradiënt van de snelheid.Een oplossing van deze momentumvergelijking geeft ons de vorm van de dynamische druk die in de vergelijking van Bernoulli verschijnt.

activiteiten:
rondleidingen

• Basisvergelijkingen voor vloeistofdynamica:

navigatie ..

Beginnersgids startpagina