Complexe Getallen: Inleiding (pagina 1 van 3)

onderdelen: een Inleiding, Activiteiten met complexen, De Abc-Formule

tot nu toe, je hebt te horen gekregen dat u niet de wortel van een negatief getal. Dat komt omdat je geen getallen had die negatief waren nadat je ze in het kwadraat had gezet (dus je kon niet “achteruit gaan” door de vierkantswortel te nemen). Elk getal was positief nadat je het kwadraat. Dus je kon niet heel goed vierkantswortel een negatief en verwachten om met iets zinnigs te komen.

nu kunt u echter de vierkantswortel van een negatief getal nemen, maar het gaat om het gebruik van een nieuw getal om het te doen. Dit nieuwe nummer werd uitgevonden (ontdekt?) rond de tijd van de Reformatie. Op dat moment geloofde niemand dat een “echte wereld” gebruik zou worden gevonden voor dit nieuwe getal, anders dan het verlichten van de berekeningen die betrokken zijn bij het oplossen van bepaalde vergelijkingen, dus het nieuwe getal werd gezien als een zogenaamd getal uitgevonden voor het gemak.

(maar als je erover nadenkt, zijn niet alle getallen uitvindingen? Het is niet alsof getallen aan bomen groeien! Ze leven in ons hoofd. We hebben ze allemaal verzonnen. Waarom niet een nieuwe uitvinden, zolang het goed werkt met wat we al hebben?)

toen:

misschien denkt u dat u dit kunt:

maar dit slaat nergens op! Je hebt al twee getallen die vierkant zijn tot 1; namelijk -1 en +1. En ik kwadraat al naar -1. Dus het is niet redelijk dat ik ook kwadraat 1 zou hebben. Dit wijst op een belangrijk detail: Bij het omgaan met fantasierijke, je iets te winnen (de mogelijkheid om te gaan met negatieven binnen vierkantswortels), maar je verliest ook iets (een deel van de flexibiliteit en handige regels die je gebruikt om te hebben bij het omgaan met vierkantswortels). In het bijzonder moet je altijd eerst het i-deel doen!

• sqrt vereenvoudigen (-9). Copyright © Elizabeth Stapel 2000-2011 All rights Reserved

(waarschuwing: de stap die door het derde” is gelijk aan “teken gaat is”“, niet”“. De i staat buiten het radicale.)

• sqrt vereenvoudigen (-25).

• Simplify sqrt(-18).

• Simplify –sqrt(-6).

In uw berekeningen zult u met i net als met x omgaan, behalve dat x2 slechts x2 is, maar i2 is -1:

• vereenvoudig 2i + 3i.

2i + 3i = (2 + 3)I = 5i

• vereenvoudig 16I – 5i.

16i-5i =(16-5) i = 11i

• vermenigvuldigen en vereenvoudigen (3i) (4i).

(3i) (4i) =(3 * 4) (i·i) = (12) (i2) = (12)(-1) = -12

• vermenigvuldigen en vereenvoudigen (i) (2i) (–3i).

(i) (2i) (–3i) = (2 · -3) (i · i · i) = (-6) (i2 · i)

=(-6) (-1 · i) = (-6) (–i) = 6i

merk dit laatste probleem op. Hierin kun je zien dat , omdat i2 = -1. Doorgaan, We krijgen:

Dit patroon van machten, tekens, 1 ’s en i’ S is een cyclus:

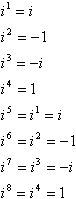
met andere woorden, om een hoog vermogen van i te berekenen, kunt u het converteren naar een lager vermogen door we nemen het dichtstbijzijnde veelvoud van 4 dat niet groter is dan de exponent en trekken dit veelvoud af van de exponent. Bijvoorbeeld, een veel voorkomende strikvraag op toetsen is iets in de trant van “Simplify I99”, het idee is dat je zult proberen om te vermenigvuldigen i negenennegentig keer en je zult geen tijd, en de leraren zullen een goede giechelen op uw kosten in de faculteit lounge. Hier is hoe de snelkoppeling werkt:

i99 = i96+3 = i (4×24)+3 = i3 = –i

dat wil zeggen, i99 = i3, omdat je de i96 gewoon kunt afkappen. (Zesennegentig is een veelvoud van vier, dus i96 is gewoon 1, wat je kunt negeren. Met andere woorden, je kunt de exponent delen door 4 (met behulp van lange deling), het antwoord verwerpen, en alleen de rest gebruiken. Dit geeft je het deel van de exponent waar je om geeft. Hier zijn nog een paar voorbeelden:

• Simplify i17.

i17 = i16 + 1 = i4 * 4 + 1 = i1 = i

• vereenvoudig i120.

i120 = i4 * 30 = i4 * 30 + 0 = i0 = 1

• vereenvoudig i64, 002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>