energetica van de vorming van ionische binding

ionische bindingen worden gevormd wanneer positief en negatief geladen ionen door elektrostatische krachten bij elkaar worden gehouden. Denk aan een enkel paar ionen, een kation en een anion. Hoe sterk zal de kracht van hun aantrekking zijn? Volgens Coulomb ‘ s wet is de energie van de elektrostatische aantrekking (\(E\)) tussen twee geladen deeltjes evenredig met de grootte van de ladingen en omgekeerd evenredig met de internucleaire afstand tussen de deeltjes (\(r\)):

\

\

waarbij de lading van elk ion wordt weergegeven door het symbool Q. de proportionaliteitsconstante k is gelijk aan 2,31 × 10-28 J * m. deze waarde van k omvat de lading van een enkel elektron (1,6022 × 10-19 C) voor elk ion. De vergelijking kan ook worden geschreven met behulp van de lading van elk ion, uitgedrukt in coulombs (C), opgenomen in de constante. In dit geval is de proportionaliteitsconstante k gelijk aan 8,999 × 109 J·M/C2. In het gegeven voorbeeld, Q1 = +1 (1,6022 × 10-19 C) en Q2 = -1(1,6022 × 10-19 C). Als Q1 en Q2 tegengestelde tekens hebben (zoals in NaCl, bijvoorbeeld, waar Q1 +1 is voor Na+ en Q2 is -1 voor Cl−), dan is E negatief, wat betekent dat energie vrijkomt wanneer tegengesteld geladen ionen van een oneindige afstand worden samengebracht om een geïsoleerd ionenpaar te vormen.

energie komt altijd vrij wanneer een binding wordt gevormd en dienovereenkomstig heeft het altijd energie nodig om een binding te breken.

zoals aangegeven door de groene kromme in de onderste helft van figuur \(\Paginindex{1}\), zou de maximale energie vrijkomen wanneer de ionen oneindig dicht bij elkaar staan, bij r = 0. Omdat ionen ruimte innemen en een structuur hebben waarbij de positieve kern wordt omgeven door elektronen, kunnen ze echter niet oneindig dicht bij elkaar staan. Op zeer korte afstanden worden afstotende elektronen–elektronen interacties tussen elektronen op aangrenzende ionen sterker dan de aantrekkelijke interacties tussen ionen met tegengestelde ladingen, zoals blijkt uit de rode kromme in de bovenste helft van figuur \(\Paginindex{1}\). De totale energie van het systeem is een balans tussen de aantrekkelijke en weerzinwekkende interacties. De paarse curve in Figuur \(\Paginindex{1}\) laat zien dat de totale energie van het systeem een minimum bereikt op r0, het punt waar de elektrostatische afstotingen en aantrekkingen precies in balans zijn. Deze afstand is dezelfde als de experimenteel gemeten bindingsafstand.

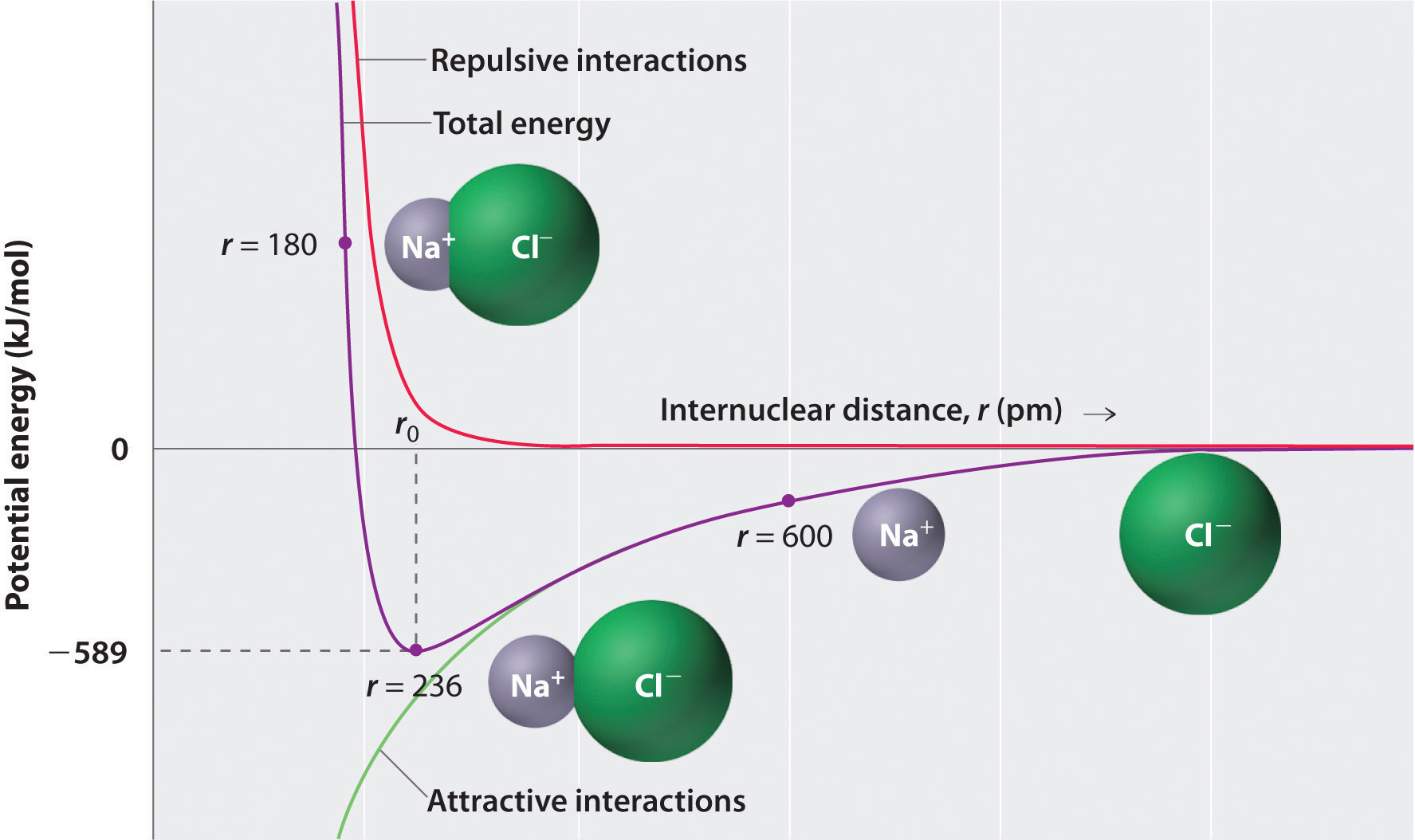
beschouw de energie die vrijkomt wanneer een gasvormig \(Na^+\) ion en een gasvormig \(Cl^-\) ion worden samengevoegd van r = ∞ tot r = r0. Aangezien de waargenomen gasfaseinterucleaire afstand 236 pm is, is de energieverandering geassocieerd met de vorming van een ionenpaar van een \(Na^+_{(g)}\) ion en een \(Cl^-_{(g)}\) ion als volgt:

\ & =(2,31 \ times {10^ {- 28}}\rm{J} \ cdot \ cancel{m}) \ left (\dfrac{( + 1)( – 1)}{236\; \cancel{pm} \ times 10^ {- 12} \ cancel{m / pm}} \right) \\ & = – 9.79 \ times 10^ {- 19}\; J / ion\; pair \ label{Eq2} \ end{align*}\]

de negatieve waarde geeft aan dat er energie vrijkomt. Onze conventie is dat als een chemisch proces energie levert aan de buitenwereld, de energieverandering negatief is. Als het energie nodig heeft, is de energieverandering positief. Om de energieverandering in de vorming van een mol NaCl-paren te berekenen, moeten we de energie per ionenpaar vermenigvuldigen met het getal van Avogadro. :

\

Dit is de energie die vrijkomt wanneer 1 mol gasvormige ionenparen wordt gevormd, niet wanneer 1 mol positieve en negatieve ionen condenseren om een kristallijn rooster te vormen. Door interacties op lange afstand in de roosterstructuur komt deze energie niet direct overeen met de roosterenergie van de kristallijne vaste stof. De grote negatieve waarde geeft echter aan dat het samenbrengen van positieve en negatieve ionen energetisch zeer gunstig is, of er nu een ionenpaar of een kristallijn rooster wordt gevormd.

we vatten de belangrijke punten over ionenbindingen samen:

• bij r0 zijn de ionen stabieler (hebben een lagere potentiële energie) dan op een oneindige internucleaire afstand. Wanneer tegenovergesteld geladen ionen worden samengebracht van R = ∞ naar r = r0, wordt de energie van het systeem verlaagd (energie wordt vrijgegeven).
• vanwege de lage potentiële energie bij r0 moet er energie aan het systeem worden toegevoegd om de ionen te scheiden. De hoeveelheid energie die nodig is, is de bindingsenergie.
• de energie van het systeem bereikt een minimum op een bepaalde internucleaire afstand (de bindingsafstand).