4-väriongelma on yksi tunnetuimmista matemaattisista ongelmista. Se vastusti todisteita yli sata vuotta ennen kuin lopulta sortui; lopulta oli olemassa pätevä todiste, mutta sellainen, joka nojasi yli tuhannen tunnin tietokoneaikaan. Jim Tilleyn tutkimuksen mukaan dramaattinen yksinkertaistaminen voisi lopulta olla mahdollista. Hän on löytänyt omaisuutta, Kempe-lukitus, että vähintään counterexample, 4-väri lause on näytteille ja on muotoillut arveluihin, jotka perustuvat laajoihin tutkimuksiin, että Birkhoff timantti on ainoa perusoikeuksien Kempe-lukitus kokoonpano.

Graafivärjäyksessä kaavioksi kutsutun matemaattisen objektin kärkipisteille osoitetaan nimilappuja eli värejä. 4-väri-ongelma edellyttäen yksi alkuperäisen motiivit kehittämiseen algebrallinen Graafiteoria. Graafista väritystä käytetään monissa reaalimaailman ongelmissa, kuten ristiriitojen minimoimisessa urheilutapahtumien aikatauluissa, tutkimusaikataulujen suunnittelussa ja istumajärjestysten järjestämisessä, jopa CCTV-kameran sijoittamisessa monikulmaiseen rakennukseen kameroiden päällekkäisyyden minimoimiseksi. Se luo myös pohjan sudokujen tekemiselle.

4-väriongelma
Francis Guthrie, kuuluisan brittiläisen matemaatikon ja loogikon Augustus De Morganin oppilas, aiheutti 4-väriongelman vuonna 1852. Hän muotoili ongelman osalta karttoja, jotka täyttävät tietyt ehdot, kuten ei sisällä mitään reikiä ja ottaa jokainen alue (esim.maa tai valtio) kytketty niin, että mitään aluetta ei ole olemassa kahdessa tai useammassa ei-vierekkäisissä osissa. Guthrie väitti, että tällaisia karttoja se ei koskaan vie enemmän kuin neljä väriä väri kartta sellainen, että ei kaksi lähialueet olivat samaa väriä.

nykyään 4-väriongelma ilmaistaan kuvaajina, ja karttojen värialueiden sijaan yksi väri vertautuu kuvaajiin. Kaikki olemassa olevat todisteet 4-väri lause osoittaa, että vähintään counterexample ei voi olla olemassa. (Vähintään counterexample on pienin planar kaavio, joka vaatii enemmän kuin neljä väriä, jotta oikea väritys sen vertices.) On otettava huomioon vain tasomaiset graafit, jotka ovat kolmiomittauksia, koska mikä tahansa kuvaaja, joka ei ole kolmiomittaus, voidaan muuttaa sellaiseksi lisäämällä reunoja. Jos tuloksena triangulation on 4-colourable, alkuperäinen kaavio on myös 4-colourable. On erittäin hyödyllistä pystyä rajoittamaan oman tarkastelun kolmikantoihin.

varhainen todistusyritys
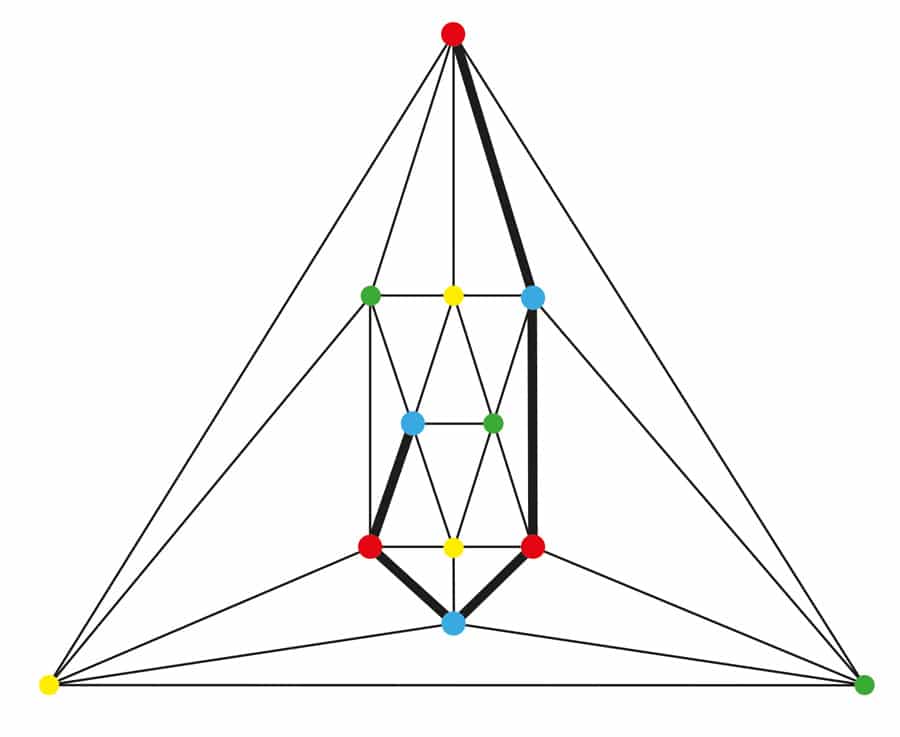
niistä, jotka tarjosivat todistusta, oli Alfred Bray Kempe, englantilainen lakimies ja amatöörimatemaatikko, henkilö, jonka mainetta hänen epäonnistunut yrityksensä tahrasi eniten. Hän ilmoitti hänen menestys vuonna 1879 ja hänen ”todiste” julkaistiin American Journal of Mathematics. Yksitoista vuotta myöhemmin kuitenkin toinen englantilainen matemaatikko Percy Heawood loi kartan, jonka hän 4-väritti lopulliselle alueelle siten, että Kempen menetelmä epäonnistui kyseiselle lopulliselle alueelle. Epäonnistumisestaan huolimatta Kempe jätti jälkeensä hyödyllisen työkalun: Kempe – ketjun. Se on maximal, kytketty (jokainen huippupiste tavoitettavissa mistä tahansa muusta, jonka polku pitkin reunoja) subgraph, jossa kaikki vertices käyttää täsmälleen kaksi väriä. Kempe-ketjut ovat osoittautuneet välineellisiksi värityksessä ja uudelleenvärityksessä. Katso Kuva 1.

olisi ällistyttävä yksinkertaistus
, Jos pelkästään birkhoffin timantti on avain 4-värisyyteen.

Proof at last
ensimmäisen pätevän todisteen julkistivat Kenneth Appel ja Wolfgang Haken vuonna 1976. Se vaati yli tuhat tuntia tietokoneen aikaa tarkistaa tiettyjä näkökohtia niiden argumentti. Tämä käsitys luottaa tietokoneen koodiin, joka mahdollisesti sisältää ihmisen aiheuttamia virheitä(ja heidän koodinsa teki!), pikemminkin kuin ”ihmisen” todiste, ei ole tyydyttänyt suurta osaa matemaattinen yhteisö. Appelin ja Hakenin todistus oli yleisrakenteeltaan elegantti, mutta yksityiskohdat rumia.

todistusta tarkensi vuonna 1996 neljän matemaatikon ryhmä: Robertson, Sanders, Seymour ja Thomas, mutta he turvautuivat yhä tietokonekoodiin todistuksensa täydentämiseksi. Vuonna 2010 Steinberger tarjosi toista muunnelmaa. Vielä ei kuitenkaan ole täysin tyydyttävää vastausta siihen, miksi 4-värin lause on tosi. (Kun konjektuuri oli osoittautunut, se sai aseman ’ lause.”)

vaihtoehtoisen todisteen etsiminen
4-väriongelma on niin helppo artikuloida ja ymmärtää, että se on herättänyt monien tuhansien amatöörimatemaatikkojen kiinnostuksen, kaikki uskovat löytävänsä yksinkertaisen klassisen todisteen ja siten tulleensa kuuluisaksi. Jim Tilleyn isä, fyysikko ja Kanadan kuninkaallisen Sotakorkeakoulun rehtori vuosina 1978-1984, oli yksi tällainen haaveilija. Aina kun hänestä tuntui, että hän oli tehnyt läpimurron, hän pyysi poikaansa Jimiä tarkistamaan työnsä. Jim löysi aina virheen. Silti, vaikka hän aluksi epäili, että hänen isänsä pyrkimyksiä olisi koskaan kantaa hedelmää, hän tuli tartunnan innostus 4-väri ongelma ja alkoi tutkia sitä intensiivisesti.

Kempe-locking
Jim Tilleyn tutkimus johti siihen, että hän löysi uuden ominaisuuden, jonka 4-värilauseen on oltava vähintään counterexample. Hän nimesi sen Kempe-lockingiksi.”Hän ymmärsi, että vähimmäistarkastusesimerkin on todennäköisesti oltava ristiriidassa toisen kiinteistön kanssa., kuinka kytketty kuvaaja on (kuinka monta vertices on poistettava kuvaajan ennen kuin se hajoaa).

Tilleyn Kempe-locking on ominaisuus, joka liittyy kolmiomittauksessa olevaan reunaan. Käsite alkaa poistamalla reuna xy vierekkäisten vertices x ja y. Jos jokaista 4-väritys tuloksena kuvaajan, jossa värit x ja y ovat samat, ei ole sekvenssi väri-interchanges, Kempe ketjut, joka aiheuttaa värin X eroaa väri y, sitten alkuperäisen kolmiomittauksen sanotaan olevan Kempe-lukittu suhteessa reunan xy. Tilley osoittautunut, että vähintään counterexample, 4-väri lause on oltava Kempe-lukittu suhteessa jokainen sen reunat, jokainen reuna vähintään counterexample on oltava tämän värin omaisuutta.

Kempe-lukitus on erityisen rajoittava ehto, jonka täyttäminen vaikeutuu kolmiomittauksen kasvaessa. Tilley lähti selvittää, onko mitään yhteistä triangulations, jotka ovat Kempe-lukittu reunat. Kempe-lockingin etsinnät johtivat hänet birkhoffin timantin luo.

birkhoffin timantti
vuonna 1913 G. D. Birkhoff havaitsi, että tietyllä kymmenen maan kokoonpanolla kartassa (kuuden maan rajarengas, joka sulkee sisäänsä neljän maan joukon) on tärkeä ominaisuus. Jos kyseinen määritys on kartassa ja jos alaosa, josta kyseinen määritys on poistettu, on 4-värinen, koko kartta on 4-värinen. Näin ollen vähimmäisvastanäyte ei voi sisältää kyseistä määritystä. Se on tullut tunnetuksi birkhoffin timanttina. Tilley havaitsi, että Kempen lukitsema reuna-XY näyttää syntyvän vasta, kun x ja y ovat myös Birkhoff-timantin graafiversion päätepisteitä. KS. Kuva 2.

konjektuuri on helposti lausuttava, ymmärrettävä ja kiehtova, ja tarjoaa pakottavan selityksen sille, miksi kaikki tasokuviot ovat 4-värisiä.

koska hän ei ollut kohdannut Kempe-locking-kokoonpanoa ilman birkhoffin timanttia, hän arveli, että birkhoffin timantti on ainoa ”perustavanlaatuinen” Kempe-locking-konfiguraatio, joka ei sisällä pienempää Kempe-locking-konfiguraatiota aligrafina. Tilley kuitenkin totesi, ettei hän pystynyt todistamaan kriittistä arveluaan. Se oli turhauttavaa, koska jos totta, konjektuuri olisi suoraan todistaa 4-väri lause. (Ollakseen vähintään counterexample, kolmiomittauksen olisi sisällettävä Birkhoff timantti subgraph, mutta jos se teki, se ei voinut olla vähintään counterexample.)

ylivoimainen tukijuttu
sen sijaan, että Tilley olisi todistanut arvailunsa, hän teki seuraavaksi parhaan teon. Hän päätti näytellä experimentalisti ja rakentaa ylivoimainen tapaus tukemaan hänen arveluihin. Hän jakoi kaikki asiaankuuluvat planar triangulations kahteen luokkaan: ne, joissa vähintään neljä vertices on poistettava ennen kuvaajat hajoavat (4-kytketty) ja ne, joissa vähintään viisi vertices on poistettava ennen kuvaajat hajoavat (5-kytketty). KS. Kuva 3. Hyödyllistä Tilleyn laajassa etsinnässä oli se, että hänen täytyi tutkia vain yhtä jäsentä kustakin isomorphism-luokasta (kaaviot, jotka ovat rakenteellisesti identtisiä). Tilley tutkittu kaikki 8044 isomorphism luokat 4-kytketty planar triangulations enintään 15 vertices ja kaikki 9733 isomorphism luokat 5-kytketty planar triangulations enintään 24 vertices. Hän löysi vain kolme Kempe-lukittua kolmiota. Jokainen löydetty Kempe-lukittu reuna esillä Birkhoff timantti ja jokainen tapahtui 4-kytketty kolmiomittauksen. Niitä ei ollut lainkaan viiden yhdistetyn kolmiomittauksen joukossa.

Tilley laajensi etsintäänsä 4-kytköksisten triangulaatioiden parissa tarkastelemalla kaikkia 30 926 isomorfismiluokkaa 16: lla verticesillä ja kaikkia 158 428 isomorfismiluokkaa 17: llä verticesillä. Laskenta-aikarajoitukset tarkoitti rajoittamalla hänen haku näytteitä 100,000 satunnaisesti luotu ei-isomorphic triangulations kunkin luokkien 18,19, ja 20 vertices. Laajennetussa haussa löytyi 45 ylimääräistä Kempe-lukittua kolmiomittausta, mutta täsmälleen samat tulokset kuin alkuperäisessä haussa: jokainen Kempe-lukittu reuna kolmiomittauksessa sisälsi siihen liittyvän Birkhoff-timantin.

mistä täältä?
Tilleyn laajat etsinnät vahvistivat helposti, että birkhoffin timantti on Kempen peruskokoonpano. Hän on testannut arvelunsa perusteellisesti, mutta se on edelleen todistamatta. Jos (tai kun) Tilleyn konjektuuri on osoittautunut todeksi, eli että birkhoffin timantti yksin on avain 4-värisyyteen, se olisi hämmästyttävä yksinkertaistus ongelmaan: yksi konfiguraatio, joka selittää kaiken – matemaattinen eleganssi.

Nelivärisen konjektuurin todistaminen vaati monien merkittävien matemaatikkojen ponnisteluja. Tilleyn arveluihin, että Birkhoff timantti on ainoa perustavanlaatuinen Kempe-locking kokoonpano voi olla vielä vaikeampi todistaa. Kokeellinen näyttö on kuitenkin vahvaa. Teoreetikot saattavat sanoa: ’miksi vaivautua?’Tilleyn vastaus on, että kyltymätön uteliaisuus voittaa: ”onhan konjektuuri helposti lausuttava, ymmärrettävä ja kiehtova, ja tarjoaa pakottavan selityksen sille, miksi kaikki tasokuviot ovat 4-värisiä.”