Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Johdanto
Neliöjuuret kirjoitetaan useimmiten käyttäen radikaalia merkkiä, kuten tämä, ![]() . Mutta on toinenkin tapa edustaa juurtumista. Voit käyttää rationaalisia eksponentteja radikaalin sijaan. Rationaalinen eksponentti on eksponentti, joka on murto-osa. Esimerkiksi
. Mutta on toinenkin tapa edustaa juurtumista. Voit käyttää rationaalisia eksponentteja radikaalin sijaan. Rationaalinen eksponentti on eksponentti, joka on murto-osa. Esimerkiksi ![]() voidaan kirjoittaa
voidaan kirjoittaa ![]() .
.
ei voi kuvitella nostavansa lukua rationaaliseksi eksponentiksi? Niihin voi olla vaikea tottua, mutta rationaaliset eksponentit voivat itse asiassa auttaa yksinkertaistamaan joitakin ongelmia. Tutkitaan rationaalisten (murto -) eksponenttien ja radikaalien välistä suhdetta.
radikaalien lausekkeiden uudelleenkirjoittaminen käyttäen Rationaalieksponentteja
radikaalit ja murtoeksponentit ovat vaihtoehtoisia tapoja ilmaista sama asia. Olette jo nähneet, miten neliöjuuret voidaan ilmaista eksponenttina yhden puolen potenssiin.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Muista, cubing numero nostaa sen potenssiin kolme. Huomaa, että näissä esimerkeissä rationaalisen eksponentin nimittäjä on luku 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and rationaaliset eksponentit: nimittäin, että luvun N: S juuri voidaan kirjoittaa joko ![]() tai
tai ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an lauseke, joka sisältää rationaalisen eksponentin, voi kirjoittaa sen uudelleen radikaalilla. Huomaa yllä olevassa taulukossa, miten rationaalisen eksponentin nimittäjä määrittää juuren indeksin. Niinpä eksponentti ![]() kääntää neliöjuurelle, eksponentti
kääntää neliöjuurelle, eksponentti ![]() kääntää viidennelle juurelle tai
kääntää viidennelle juurelle tai ![]() ja
ja ![]() kääntää kahdeksannelle juurelle tai
kääntää kahdeksannelle juurelle tai ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
Kirjoita lauseke uudelleen murtoluvun eksponentin ollessa radikaali. Murtoluvun nimittäjä määrää juuren, tässä tapauksessa kuution juuren. suluissa |
|
|
vastaus |
td> |
|
muista, että eksponentit viittaavat vain välittömästi vasemmalla olevaan suureeseen, ellei käytetä ryhmittelytunnusta. Alla oleva esimerkki näyttää hyvin samanlaiselta kuin edellinen esimerkki, jossa on yksi tärkeä ero-sulkeita ei ole! Katso, mitä tapahtuu.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Murtoluvun nimittäjä määrää juuren, tässä tapauksessa kuution juuren. eksponentti viittaa vain eksponentin välittömästi vasemmalla puolella olevaan lausekkeen osaan, tässä tapauksessa x: ään, mutta ei 2: een. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. Tällöin radikaalin indeksi on 3, joten rationaalieksponentti on koska 4 on radikaalin ulkopuolella, se ei sisälly ryhmittelymerkkiin eikä eksponentti viittaa siihen. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
vastaus |
|
|
rationaaliset eksponentit, joiden osoittajat ovat muita kuin yksi
kaikki edellä olevissa esimerkeissä olevat murtoluvun eksponenttien osoittajat olivat 1. Voit käyttää murto-eksponentteja, joilla on muita osoittajia kuin 1 ilmaista juuria, kuten alla. Huomaatko mitään kuvioita tässä taulukossa?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
kirjoittaa radikaali murtoluvun eksponentin avulla, jolloin potenssista, johon radikandi nostetaan, tulee osoittaja ja juuresta nimittäjä.
kirjoitetaan murtoluvun eksponentteja
mikä tahansa radikaali muodossa ![]() voidaan kirjoittaa murtoluvun eksponentilla muodossa
voidaan kirjoittaa murtoluvun eksponentilla muodossa ![]() .
.
![]() ja
ja ![]() suhde toimii rationaalisille eksponenteille, joiden osoittaja on myös 1. Esimerkiksi radikaali
suhde toimii rationaalisille eksponenteille, joiden osoittaja on myös 1. Esimerkiksi radikaali ![]() voidaan kirjoittaa myös muodossa
voidaan kirjoittaa myös muodossa ![]() , koska mikä tahansa luku pysyy samana arvona, jos se nostetaan ensimmäiseen potenssiin. Nyt voit nähdä, mistä Osoittaja 1 tulee vastaavassa muodossa
, koska mikä tahansa luku pysyy samana arvona, jos se nostetaan ensimmäiseen potenssiin. Nyt voit nähdä, mistä Osoittaja 1 tulee vastaavassa muodossa ![]() .
.
yksinkertaistetaan radikaaleja ilmaisuja käyttämällä rationaalisia eksponentteja ja eksponenttien lakeja
tutkitaan nyt joitakin radikaaleja ilmaisuja ja katsotaan, miten niitä voidaan yksinkertaistaa. Tässä radikaali ilmaisu, joka kaipaa yksinkertaistamista, ![]() .
.
eräs tapa yksinkertaistaa tätä lauseketta on A3: n ryhmien kertoimiminen ja vetäminen esiin, kuten tässä esimerkissä on esitetty.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
vastaus |
|
|
tätä ilmaisua voi myös yksinkertaistaa ajattelemalla radikaalia lausekkeena, jolla on rationaalinen eksponentti, ja käyttämällä periaatetta, että mikä tahansa radikaali muodossa ![]() voidaan kirjoittaa murtoluvun eksponentilla muodossa
voidaan kirjoittaa murtoluvun eksponentilla muodossa![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
molemmat yksinkertaistamismenetelmät antoivat saman tuloksen, a2. Riippuen asiayhteydestä ongelma, se voi olla helpompi käyttää yhtä menetelmää tai muita, mutta nyt, huomaat, että olet voinut yksinkertaistaa tätä lauseketta nopeammin käyttämällä rationaalinen eksponentit kuin käytettäessä ”pull-out” menetelmä.
kokeillaan toista esimerkkiä.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the rationaalinen eksponentti takaisin radikaaliin muotoon. |
|
|
vastaus |
|
|
jälleen vaihtoehtoisena menetelmänä on pyrkiä yksinkertaistamaan radikaalia factoringin avulla. Juuri ratkaisemasi esimerkki näyttää tältä.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
kokeillaan monimutkaisempaa lauseketta, ![]() . Tässä lausekkeessa on kaksi muuttujaa, murtoluku ja radikaali. Otetaan se askel askeleelta ja katsotaan, jos käyttämällä murto exponents voi auttaa meitä yksinkertaistamaan sitä.
. Tässä lausekkeessa on kaksi muuttujaa, murtoluku ja radikaali. Otetaan se askel askeleelta ja katsotaan, jos käyttämällä murto exponents voi auttaa meitä yksinkertaistamaan sitä.
aloitetaan yksinkertaistamalla nimittäjää, sillä tässä radikaali merkki sijaitsee.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Konventionaalisesti lauseketta ei yleensä pidetä yksinkertaistettuna, jos sillä on nimittäjässä murto-eksponentti tai radikaali. |
||
|
vastaus |
|
||
no, se kesti hetken, mutta teit sen. Sovelsit sitä, mitä tiedät murtoluvun eksponenteista, negatiivisista eksponenteista ja eksponenttien säännöistä yksinkertaistaaksesi ilmaisua.
Summary
radikaali voidaan ilmaista lausekkeena, jonka eksponentti on murto-osa seuraamalla konventiota ![]() . Radikaalien uudelleenkirjoittaminen murto-eksponenteilla voi olla hyödyllistä joidenkin radikaalien lausekkeiden yksinkertaistamisessa. Kun työskentelet murtoluvun eksponenttien kanssa, muista, että murtoluvun eksponentteihin sovelletaan kaikkia samoja sääntöjä kuin muihinkin eksponentteihin, kun ne esiintyvät algebrallisissa lausekkeissa.
. Radikaalien uudelleenkirjoittaminen murto-eksponenteilla voi olla hyödyllistä joidenkin radikaalien lausekkeiden yksinkertaistamisessa. Kun työskentelet murtoluvun eksponenttien kanssa, muista, että murtoluvun eksponentteihin sovelletaan kaikkia samoja sääntöjä kuin muihinkin eksponentteihin, kun ne esiintyvät algebrallisissa lausekkeissa.
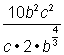
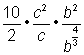
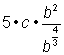
Leave a Reply