Jason McCormick
apulaisprofessori, siviili & Environmental Engineering, University of Michigan, Ann Arbor, MI, USA

suorakulmaisista ja neliömäisistä ontoista rakennepalikoista (HSS) tehdyt Momenttiyhteydet ovat saaneet vähemmän vastiketta kuin aksiaalisesti kuormitetuista jäsenistä (T -, Y -, cross -, and K-yhteydet). Suurin osa näihin yhteyksiin keskittyvistä staattisista tutkimuksista on tarkastellut Vierendeelin ristikkojärjestelmiä. Nämä systeemit muodostuvat usein neliömäisistä tai suorakulmaisista ylä-ja alaäänistä, jotka ovat yhteydessä neliömäisiin tai suorakulmaisiin pystysuuntaisiin rainan (haaran) jäseniin (Kuva 1). Tämän konfiguraation seurauksena chord-to-web-yhteys taipuu merkittävästi leikkaus-ja aksiaalikuormitusten mukana, eikä sitä pidetä puristettuna yhteytenä, kuten tyypillisissä ristikkojärjestelmissä yleensä tehdään. Alun perin suunniteltu vuonna 1896 Arthur Vierendeel, se oli vasta HSS kehitettiin, että mahdollisuudet Vierendeel trusses alkoi toteutua (Korol et al. 1977), mutta niiden käyttö vaati ymmärrystä siitä, miten momentti siirretään HSS-to-HSS t-yhteyksien välillä.

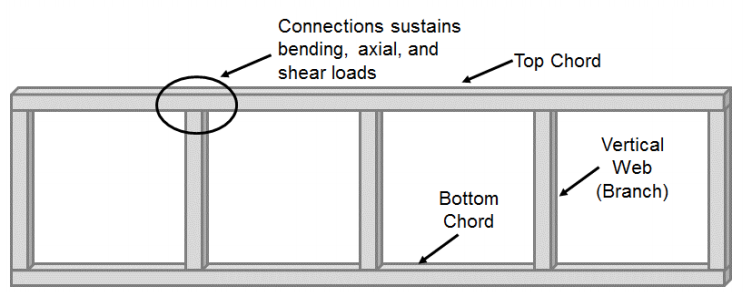
monet näiden yhteyksien varhaisista tutkimuksista keskittyivät yhteyden kykyyn kehittää haarajäsenen koko momenttikapasiteettia. Jubb and Redwood (1966) osoitti, että kun haaraosan leveys oli yhtä suuri kuin sointuosan (β=1), HSS: n jäsenen koko momenttikapasiteetti voitiin saavuttaa ilman vahvistusta. Tässä tutkimuksessa ei kuitenkaan otettu huomioon momenttikapasiteetin mahdollista menetystä aksiaalikuormituksen vuoksi. Toisaalta, Korol et al. (1977) osoitti, että yhteydet pienempi haara leveys kuin sointu ei voinut kehittää koko momentti kapasiteetti haara vahvistamatta läpi sarjan 29 eri yhteyskokeita ottaen huomioon 5 eri kokoonpanoissa (vahvistamaton, haara laippa vahvistuslevyt, sointu laippa jäykisteet, haunch, ja katkaistu pyramidi). Yleensä vahvistamattomien Vierendeel-tyyppisten liitäntöjen lujuus ja jäykkyys vähenevät soinnun slenderness-suhteen (B/t) kasvaessa ja haara-soinnun leveyssuhteen (β) pienentyessä. Tämän seurauksena kuumentamattomia vierendeel-ristikkotyyppisiä yhteyksiä voidaan pitää jäykkinä (eli ne kiertyvät minimaalisesti soinnun ja haaran välillä) vain silloin, kun haaran ja soinnun välinen leveyssuhde on 1,0 ja soinnun slenderness-suhde on alhainen tai yhteys on vahvistettu (Packer 1993).

koska näiden liitosten maksimimomentit voivat tapahtua liian suurissa muodonmuutoksissa, käytetään samanlaista lähestymistapaa kuin aksiaalisesti kuormitetuissa neliö-ja suorakulmaisissa HSS-liitoksissa, joissa käytetään lopullista kantavuutta tai muodonmuutos-tai pyörimisrajaa suunnittelumomentin kuvaamiseen (Wardenier 1982). AISC 360-10 (luku K3) tarkastelee kolmea raja-tilaa neliö-ja suorakaiteen muotoisille HSS T-liitoksille staattisessa tasossa taivuttelussa: sointuseinän muovitus, sivuseinän paikallinen taipuminen ja haaran paikallinen taipuminen epätasaisen kuormituksen jakautumisen vuoksi. Sointuseinän plastisoituminen johtuu siitä, että haaraosan leveys on pienempi kuin soinnun leveys (β ≤ 0,85), mikä edellyttää taivutusmomentin tuottamien jännitys-ja puristuskuormien siirtämistä soinnun suhteellisen joustavan pinnan kautta eikä suoraan jäykemmille sivuseinille. Rajatilayhtälö (AISC 360-10 yhtälö K3-6) voidaan johtaa myötölinjateoriasta (kuva 2):

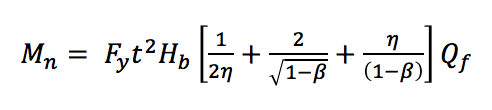
Mn on liitoksen nimellinen momenttikapasiteetti, Fy on soinnun määritelty pienin myötölujuus, Hb on haaran Kokonaiskorkeus, h on kuormituspituusparametri, joka vastaa haaran korkeutta jaettuna soinnun leveydellä (olettaen, että soinnun ja haaraosan välinen kulma on 90o kuten vierendeelille on tyypillistä trusses), ja QF on parametri, joka vähentää nivelen kapasiteettia aksiaalisen puristuksen läsnä ollessa sointuun.

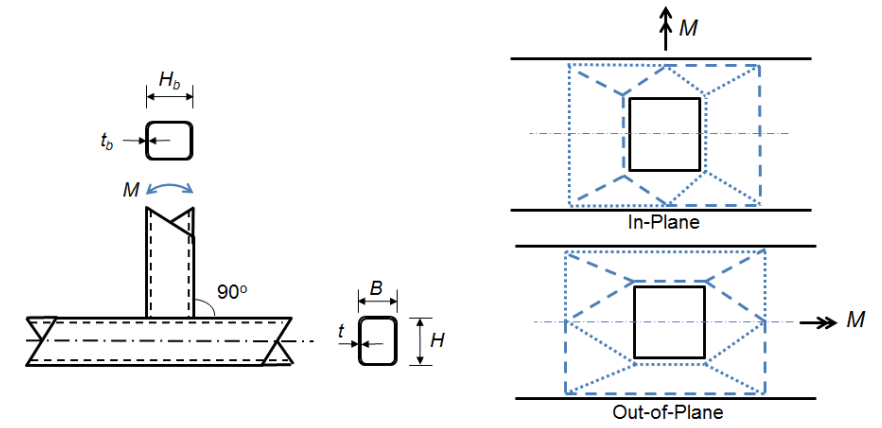
kaksi muuta rajatilaa liittyvät yhteyksiin, joissa haaran jäsenen leveys on yhtä suuri tai lähes yhtä suuri kuin soinnun leveys (β > 0.85) eli haaraosan laipoissa kehitetyt jännitys-ja Puristuskuormat siirtyvät lähes suoraan soinnun jäykempiin sivuseiniin. T-liitoksen sivuseinän paikallisen saannon raja-arvo (AISC 360-10-yhtälö K3-7) voidaan johtaa web-paikallisesta saannon yhtälöstä keskitetyille voimille, joita sovelletaan kauempana jäsenen päästä kuin sen syvyys (AISC 360-10-yhtälö J10-2):

mn = 0.5Fyt(HB + 5t)2
yhtälö 2

kun haaran paikallinen taipuminen johtuu epätasaisesta kuormitusjakaumasta (AISC 360-10 yhtälö K3-8) T-liitoksessa käytetään tehokasta leveyslähestymistapaa, jolla jäykistäjän kapasiteettia vähennetään ahdin soveltaman nimellismomentin saamiseksi:

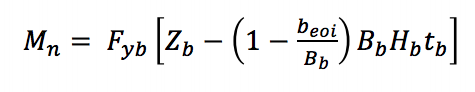
FYB on haaran määritelty pienin myötölujuus, Zb on oksan muoviosamoduuli taivutusakselin ympäri, beoi on oksan efektiivinen leveys, Bb on oksan kokonaisleveys ja tb on haaran mitoitettu seinämän paksuus.

koska on olemassa rajoitetusti kokeellista näyttöä tukemaan erityisiä suunnittelumalleja Vierendeel ristikko yhteydet (t-yhteydet) alle out-of-plane taivutus, analogiset raja-tilat kuin ne In-plane taivutus käytetään (Packer et al. 2010). Yksi soinnun distortionaalisen vikaantumisen ylimääräinen raja-tila kehittyy siitä vääntömomentista, jota haaraosapuoli kohdistaa soinnulle tason ulkopuolisen momentin seurauksena. Tämä vääntömomentti voi johtaa soinnun vinoon. Tason ulkopuolisen taivutuksen nimellismomenttiyhtälöt löytyvät AISC 360-10-yhtälöistä K3-9, K3-10, K3-11 ja K3-12. Yhtälöt sekä In-plane ja out-of-plane taivutus T-yhteydet ovat samanlaisia kuin ne, jotka on hyväksytty kansainvälisesti (Packer et al. 2010).

edellä mainitut suunnitteluyhtälöt johdettiin ottaen huomioon vierendeelin ristikkojärjestelmät staattisissa kuormituksissa. Tuore tutkimus (Fadden et al. 2015) on edistänyt tätä työtä pohtiakseen neliö-ja suorakulmaisten HSS-to-HSS-momenttiyhteyksien käyttäytymistä suurissa syklisissä kuormituksissa käytettäväksi putkipohjaisissa seismisissä momenttikehysjärjestelmissä (väli-ja erikoismomenttikehyksissä). Tällainen järjestelmä näyttää hyödyntävän erinomaisia aksiaalinen, taivutus, ja vääntö ominaisuuksia, korkea lujuus-paino-suhde, ja arkkitehtonisesti miellyttävä luonne neliön ja suorakaiteen HSS. Suuri vääntövastus voi johtaa säteen sivusuuntaisen piristymisen vähenemiseen, kun taas suuri lujuus-paino-suhde johtaa pienempään seismiseen massaan. Tällaisten liitäntöjen on kuitenkin kyettävä käymään läpi palkin jäsenen stabiili Muovinen ripustus, jossa 80% palkin jäsenen muovikapasiteetista säilyy joko 0,2 rad. (IMF) tai 0,4 rad. (SMF) of inter-story drift (AISC 341-10). Koska nykyinen seisminen suunnittelu moment frame järjestelmien edellyttää suurin osa inelastic käyttäytymistä esiintyy palkki jäsen, palkki jäsen myös on saavutettava täyden muovikapasiteetin ennen kuin tehdään paikallisia buckling. Fadden ja McCormick (2014a) tarkastelivat sekä kokeellisia että äärellisiä elementtimalleja, joiden avulla voidaan määrittää taivutettavan HSS: n leveys-paksuus-ja syvyyspaksuusvaatimukset, koska nykyisen AISC Seismic Provisions (AISC 341-10) – standardin mukaiset vaatimukset kehitettiin pitkälti syklisten aksiaalisesti kuormitettujen HSS: n jäsenten testien perusteella.

sopivien kokoonpanojen ja yksityiskohtaisten vaatimusten määrittämiseksi tämän lujuuden ja sitkeyden vaatimuksen täyttämiseksi testattiin kokeellisesti neljää eri liitäntäkonfiguraatiota: kaksi suoraan hitsattua vahvistamatonta liitäntää (verrattomat ja yhteensopivat) ja kaksi vahvistettua liitäntää (levyn ja ulkoisen kalvolevyn kautta). Kaikki yhteydet käytetään HSS 10X10X5/8 sarake. Suoraan hitsatuissa liitoksissa hyödynnettiin AWS D1.1 (2010) – standardin mukaisia valmiiksi koulutettuja CJP-hitsejä. Verrattomassa liitoksessa säde oli HSS 12X8X3 / 8 (β = 0.8) viittaa siihen, että pylvään kasvojen plastisoituminen voi olla huolenaihe. Sovitetussa liitoksessa palkki oli HSS 12X10X3 / 8 (β = 1.0), joka mahdollisti kuormien siirtämisen suoraan sivupintaan. Liitosten lataamiseen käytettiin AISC-latausprotokollaa (AISC 341-10) seismisten momenttiyhteyksien esikvalifiointia varten. Yhteyksien käyttäytyminen oli odotetusti verrattoman yhteyden osoittaessa muodonmuutoksia sarakkeen pinnalla, kun taas sovitettu yhteys pystyi siirtämään kuorman sarakkeen sivuseiniin. Molemmat liitokset kuitenkin pettivät hitsin kulman kärkiosassa olevan pylvään perusmetallin murtuman vuoksi (kuva 3). Tämä hauras vika rotaatioissa 0,4 rad. ja 0,5 rad. vastaavasti vahvisti, että suoraan hitsatut liitokset eivät tarjoa sopivaa käyttäytymistä seismisille sovelluksille.

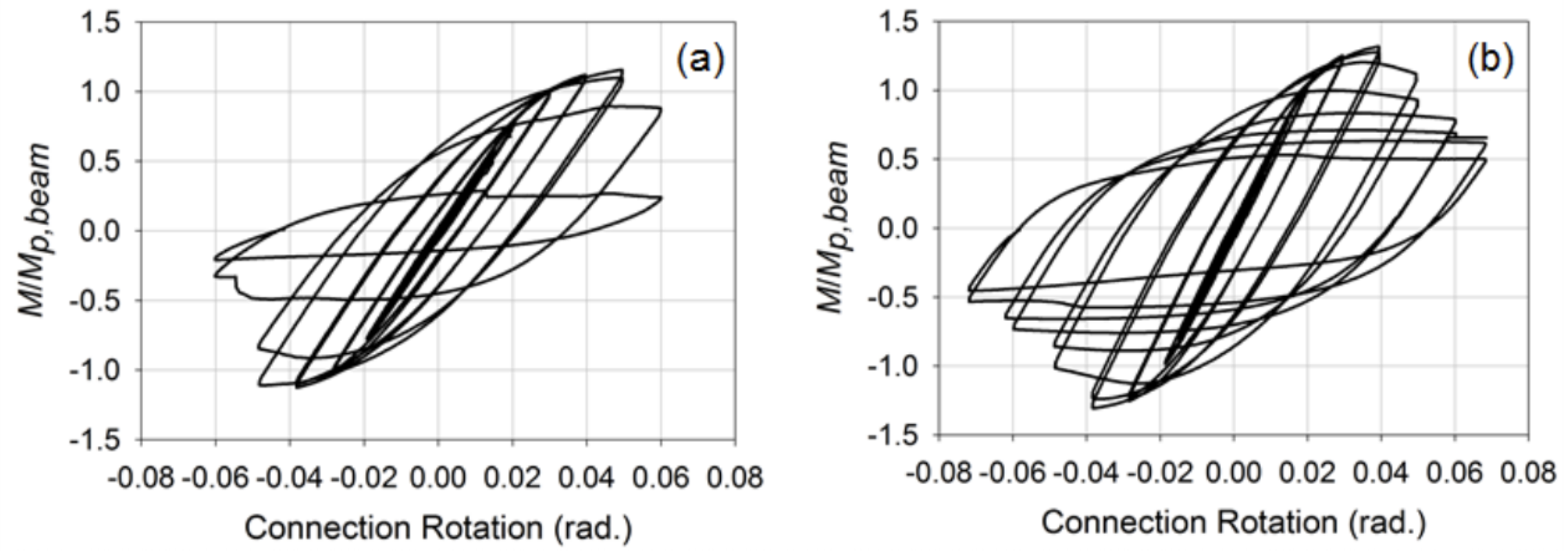
vahvistetut liitännät kehitettiin sen jälkeen ottaen huomioon levy-ja ulkopuoliset kalvolevyt, joita käytetään usein leveissä laippapalkki-HSS-pylväskytkennöissä, jotta saatiin parempi mekanismi jännitys-ja puristusvoimien siirtämiseksi pylvään sivuseinään ja hitseihin asetettujen jännityspitoisuuksien minimoimiseksi. Näissä liitoksissa palkit olivat HSS 12x8x3 / 8 (β = 0,8) – jäseniä. Tiedot erityisestä menettelystä, jota käytetään suunniteltaessa ja yksityiskohtaisesti näitä yhteyksiä löytyy Fadden and McCormick (2014b) ja Fadden et al. (2015). Samassa kuormituksessa kuin vahvistamattomat Liitännät, Liitännät osoittivat vakaampaa käyttäytymistä muovisen saranan esiintyessä poispäin pylvään pinnasta läpivienti-tai ulkokalvo-levyn päässä (Kuva 4). Molemmat yhteydet pystyivät myös 0,4 rad. pyöriminen ennen paikallista vääntymistä, mikä johti momenttikapasiteetin heikkenemiseen. Kuitenkin, murtuma ei aloittaa kulmassa HSS palkki koska pyöräily suurilla kierto tasoilla 0,7 rad. Sovitettujen ja ulkoisten kalvolevyliitosten normalisoitujen momenttikiertokäyrien vertailu on nähtävissä kuvassa 5. Kaiken kaikkiaan vahvistetut yhteydet osoittivat lupausta HSS-to-HSS seismisten momenttirunkojärjestelmien käytölle, mutta enemmän työtä tarvitaan näiden yhteyksien siirtämiseksi kohti lopullista prequalification.

AISC. (2010). Seismic Provisions for Structural Steel Buildings. ANSI / AISC 341-10. American Institute of Steel Construction, Chicago, IL.

AISC. (2010). ”Teräsrakenteiden TEKNISET TIEDOT”. ANSI / AISC 360-10. American Institute of Steel Construction, Chicago, IL.

AWS. (2010). ”Structural Welding Code”). ANSI / AWS D1. 1, American Welding Society, Miami, FL.

Fadden, F. ja McCormick, J. (2014a). ”Finite Element Model of the Cyclic Bending Behavior of Hollow Structural Sections”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. and McCormick, J. (2014b). ”HSS-to-HSS Seismic Moment Connection Performance and Design”. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., and McCormick, J. (2015). ”Cyclic Testing of Welded HSS-to-HSS Moment Connections for Seismic Applications”. ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J. E. M. and Redwood, R. G. (1966). ”Liitosten suunnittelu lokeroihin”. The Institution of Structural Engineers, Conference on Industrialized Building and the Structural Engineer, Institute of Structural Engineers, Lontoo.

Korol, R. M., El-Zanaty, M., and Brady, F. J. (1977). Vierendeelin ristikoiden neliönmuotoisten Rakenneputkien epätasa-arvoiset liitokset. Canadian Journal of Civil Engineering, 4, 190-201.

Packer, J. A. (1993). Momenttiyhteydet suorakulmaisten Rakenneputkien välillä. Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. ja Kurobane, Y. (2010). Suunnitteluohje 3: suorakulmaisiin Rakenneputkisiin (RHS) liitoksiin pääasiassa staattisessa kuormituksessa 2.Painos. CIDECT, Kanada.

Wardenier, J. (1982). ”Hollow Section Liitokset”. Delft University Press, Delft, Alankomaat.

syyskuu 2016

Lataa PDF