voimaa voidaan ajatella työntönä tai puskuna tiettyyn suuntaan. Kun kappaleeseen kohdistetaan voima, siitä aiheutuva kappaleen liike riippuu siitä, mihin voima kohdistuu ja miten kappale rajoittuu.Jos kappale on epäyhtenäinen ja voima kohdistuu painovoiman keskipisteen kautta,kappale liikkuu Newtonin liikelakien kuvaamassa puretranslaatiossa.Jos objekti on rajoitettu (tai kiinnitetty) johonkin apivot-nimiseen paikkaan, objekti suojautuu pivotista, mutta ei käännä.Voima välittyy Pivotin kautta ja pyörimisen yksityiskohdat riippuvat siitä, kuinka kaukana kohdistettu voima on pivotista.Jos kappale on unconfined ja voima kohdistetaan somedissistanssiin painopisteestä, kappale sekä translatoi että pyörii painopisteen ympäri.Pyörimisen yksityiskohdat riippuvat etäisyydestäsovelletusta voimasta painopisteeseen.Lentävien esineiden liike onkuvattu tämän kolmannen liiketyypin mukaan; käännöksen ja rotaation yhdistelmä.

voima F on avektorisuure,eli siihen liittyy sekä magnitudi että suunta. Forcen johtaminen on tärkeää, koska objektin tuloksena oleva liike on samaan suuntaan kuin voima.Voiman Tulo ja kohtisuora etäisyys painovoiman keskipisteeseen,kun kyseessä on kiintymätön kappale, tai kääntöpisteeseen, kun kyseessä on rajoitettu kappale, merkitään momentiksi tai momentiksi.Vääntömomentti on myös vektorisuure ja tuottaa rotaation samalla tavalla kuin voima tuottaa translaation. Nimittäin objekti atrest, tai pyörivät vakio kulmanopeus, jatkaa tehdä sountil se on riippuvainen ulkoisen vääntömomentin. Vääntömomentti tuottaa muuttuvan kulmanopeuden, jota kutsutaan kulmakiihtyvyydeksi.

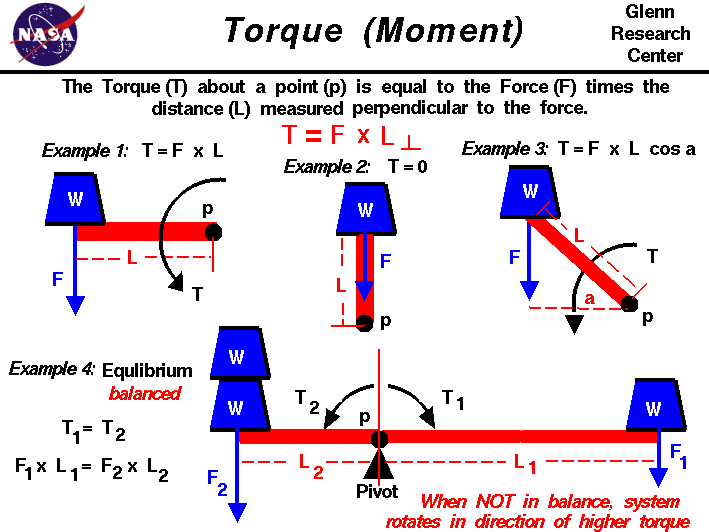
vääntömomentin t määrittämiseen käytetty etäisyys L on etäisyys pivot P: stä voimaan, mutta mitattuna kohtisuorassa voiman suuntaukseen nähden.On luku, näytämme neljä esimerkkiä vääntömomentit havainnollistaa perusperiaatteita koskevat torques.In jokaisessa esimerkissä sininen paino W toimii punaisella palkilla, jota kutsutaan nimellä tankovarsi.

esimerkissä 1 voima (paino) kohdistetaan kohtisuoraan käsivarteen. Tällöin kohtisuora etäisyys on tangon pituus ja vääntömomentti on yhtä suuri kuin pituuden ja voiman tulo.

esimerkissä 2 sama voima kohdistuu käsivarteen, mutta voima vaikuttaa nyt suoraan Pivotin läpi. Tällöin etäisyys pivot kohtisuorassa forceis nolla. Tässäkin tapauksessa vääntömomentti on siis nolla.Ajattele saranaovea. Jos painat oven reunaa kohti saranaa, ovi ei liiku, koska vääntömomentti on nolla.

esimerkki 3 on yleinen tapaus, jossa voimaa sovelletaan jossakin a-kulmassa käsivarteen nähden. Kohtisuora etäisyys annetaan bytrigonometryas pituus varren (L)kertaa thecosiini (cos) kulman.Vääntömomentti saadaan näin:

esimerkit 1 ja 2 voidaan johtaa tästä yleisestä kaavasta,koska 0 asteen kosini on 1,0 (Esimerkki 1) ja 90 asteen kosini on 0,0 (Esimerkki 2).

esimerkissä 4 pivot on siirretty tangon päästä lähelle tankoa. Painot lisätään molemmille puolille pivot.To yksi paino w tuottaa voiman F1, joka toimii etäisyydellä L1 pivotista. Tämä luo vääntömomentin T1 yhtä suuri kuin voima ja etäisyys.

vasemmalla pivotista kaksi painoa w tuottaa voiman F2 etäisyydellä L2.Tämä tuottaa vääntömomentin T2 vastakkaiseen suuntaan kuin T1, koska etäisyys on vastakkaiseen suuntaan.

Jos systeemi olisi tasapainossa eli tasapainossa,vääntömomentit olisivat yhtä suuret eikä nettovääntömomentti vaikuttaisi systeemiin.

Jos systeemi ei ole tasapainotilassa tai epätasapainossa, tanko pyörähtää nivelen ympäri suuremman vääntömomentin suuntaan.Jos F2 = 2 * F1, mikä on L1: n ja L2: n suhde systeemin tasapainottamiseksi? Jos F2 = 2 * F1 ja L1 = L2,mihin suuntaan systeemi pyörisi?

Ilmailuinsinöörit käyttävät aerodynaamisen pinnan tuottamaa vääntömomenttia lentokoneiden vakauttamiseen ja ohjaamiseen.Lentokoneissa ohjauspinnat tuottavatdynaamiset voimat.Nämä voimat kohdistetaan jonkin matkan päähän lentokoneen cg: stä, minkä vuoksi ilma-alus pyörii. Theelevators tuottaa apitching moment, therudder tuottaa ayawing moment, ja theailerons tuottaa arolling moment. Kyky vaihdella voiman määrää ja hetkeä antaa lentäjälle mahdollisuuden ohjailla tai totella konetta.Pienoismalliraketeissa moottoreita käytetään tuottamaan vääntöä painovoiman rakettikeskuksesta, joka tarjoaa toimintakyvyn moottorilennon aikana.Leijoissa aerodynaaminen ja painollinen voima tuottavat vääntömomentin Bridle-pisteen suhteen.Etäisyys suitsipisteestä ja joukkojen suuruus vaikuttavat voimakkaasti leijan suorituskykyyn.

toiminta:
opastukset

• voimat, vääntö ja liike:

lentokoneen perusliike:

• ilma-aluksen Rullausliike:

ilma-aluksen pituusliike: ilma-aluksen kääntöliike:

• siivekkeet:

Spoilerit:

• elevators:

stabilaattorit:

• peräsin:

pysyvyys malliraketti:

navigointi..

aloittelijan oppaan kotisivu