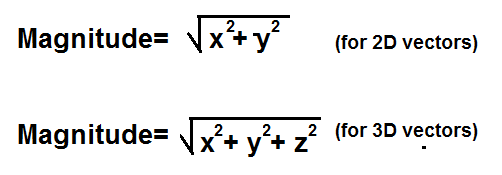
Tämä Magnitudilaskuri laskee vektorin magnitudin vektorin 2-tai 3-ulotteisten arvojen perusteella.

tällä laskijalla voidaan laskea sekä 2D-että 3D-vektorien suuruus. 2D-vektorin magnitudin laskemiseksi käyttäjä vain syöttää vektorin x-ja y-arvot ja jättää kolmannen kentän, z-arvon, tyhjäksi. 3D-vektorin magnitudin laskemiseksi käyttäjä syöttää kaikkiin 3-muotoisiin kenttiin vektorin x, y ja z arvot.

yhtäkään yksikköä ei tarvitse määritellä ratkaistaessa magnitudia. Laskettava tuloksellinen Suure on samassa yksikössä kuin vektoriarvon inputofin yksikkö. Jos siis lasketaan voimavektorin magnitudi ja syötetään vektorin komponentit newtoneiksi (N), saadaan myös tuloksena oleva magnitudi yksikkö newtoneiksi.

magnitudin laskeminen on vektorin hyvin merkittävä laskutoimitus. Magnitudi kuvaa vektorin nettosalaarin kokonaisarvoa. Eli esimerkiksi jos voimavektori on 3i +4j + 0k N, sen iskuvoima on 5 newtonia voimaa.

monet insinööriyksiköt on määritelty vektoreina. Arvot, kuten voima, magneettikenttä, nopeus jne. on määritelty vektoriarvoilla. Tämä johtuu siitä, että näillä yksiköillä ei ole vain suuruutta, vaan niillä on myös suunta. Voima kohdistetaan tietyllä työntö-tai vetokerralla, mutta se ei koostu vain suuruudesta. Se on myös annettu tiettyyn suuntaan. Voima voidaan sovellaakorkeus pystysuoraan alaspäin, sovelletaan 45° kulmassa, 50° kulmassa, ja niin edelleen. Mikä kulma sitä sovelletaan muuttaa nettotulos toimintaa, joka tapahtuu. Kun ratkaisemme vektorin magnitudin, ratkaisemme yksinkertaisesti sen nettosalaarin arvon, jonka vektori tuottaa.

esimerkkilaskelmat
laske vektorin magnitudi 5I – 7j +9k.

laskenta:
tuloksellinen magnitudi: 12.45

laske vektorin magnitudi 3i – 14J – 21k.

laskenta:
tuloksellinen magnitudi: 25.42