yhden muuttujan lineaarisen epäyhtälön kuvaaja on lukujono. Käytä avointa ympyrää < ja > ja suljettua ympyrää ≤ ja ≥.

x > -3

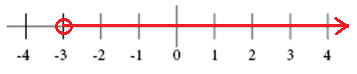
x ≥ 2

samaa ratkaisua kutsutaan ekvivalentiksi. On olemassa ominaisuuksia eriarvoisuutta sekä oli ominaisuuksia tasa-arvo. Kaikki alla olevat ominaisuudet koskevat myös epätasa-arvoa, johon liittyy ≥ ja ≤.

epäyhtälön yhteenlaskuominaisuus sanoo, että saman luvun lisääminen epäyhtälön kummallekin puolelle tuottaa ekvivalentin epäyhtälön

$$If \: x>y,\: then\: x+z>y+z$$

$$If\: x<y,\: then\: x + z<y+z$$

epäyhtälön vähennysominaisuus kertoo, että saman luvun vähentäminen epäyhtälön molemmilta puolilta antaa ekvivalentin epäyhtälön.

$$If \: x>y,\: then\: x-z>y-z$$

$$If\: x<y,\: then\: x-z<y-z$$

epäyhtälön kertolaskuominaisuus kertoo, että kertolasku positiivisen luvun epäyhtälön molemmin puolin tuottaa ekvivalentin epäyhtälön.

$$If\: x>y \: ja\: z>0,\: then\: xz>yz$$

$$If\: x<y\: and\: z>0,\: silloin\: XZ<YZ$$

kertolasku epäyhtälön kummallakin puolella negatiivisella luvulla ei tuota vastaavaa epäyhtälöä, ellei käännetä myös epäyhtälön symbolin suuntaa

$$If \: X>y \: and\: Z<0,\: then\: XZ<YZ$$

$$If\: X<Y\: ja\: z<0,\: then\: xz>yz$

sama pätee epäyhtälön jakoomaisuuteen.

jako epäyhtälön molemmin puolin, joilla on positiivinen luku, tuottaa vastaavan epäyhtälön.

$$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x<Y\: and\: z>0,\: then\: \frac{x}{z}<\frac{y}{z}$$

ja jako negatiivisen luvun epäyhtälön molemmin puolin tuottaa vastaavan epäyhtälön, jos epäyhtälön symboli on käänteinen.

$$If \: x>y \: and\: z<0,\: then\: \frac{x}{z}<\frac{y}{z}$$

$$If\: x<Y\: and\: z<0,\: then\: \frac{x}{z}>\frac{y}{z}$$

ratkaistaksesi monivaiheisen epäyhtälön teet samoin kuin ratkaistessasi monivaiheyhtälöitä. Otetaan yksi asia kerrallaan mieluiten aloittamalla eristämällä muuttuja vakioista. Monivaiheista epätasa-arvoa ratkaistaessa on tärkeää muistaa kääntää epäyhtälön merkki kerrottaessa tai jaettaessa negatiivisilla luvuilla.

esimerkki

ratkaise epäyhtälö

$$-2\left ( x+3 \right )<10$$