opetusohjelma selittää regressioanalyysin perusteet ja näyttää muutamia erilaisia tapoja tehdä lineaarinen regressio Excelissä.

kuvittele tämä: sinulle tarjotaan paljon erilaista dataa ja sinua pyydetään ennustamaan yrityksesi ensi vuoden myyntiluvut. Olette löytäneet kymmeniä, ehkä jopa satoja tekijöitä, jotka voivat mahdollisesti vaikuttaa lukuihin. Mutta mistä tietää, mitkä niistä ovat oikeasti tärkeitä? Suorita regressioanalyysi Excelissä. Se antaa sinulle vastauksen tähän ja moniin muihin kysymyksiin: Millä tekijöillä on merkitystä ja mitkä voidaan jättää huomiotta? Miten läheisesti nämä tekijät liittyvät toisiinsa? Ja kuinka varma voit olla ennusteista?

• regressioanalyysi Excelissä
• lineaarinen regressioanalyysi Excelissä Analyysityökalulla Pak
• Piirrä lineaarinen regressiografia
• regressioanalyysi Excelissä kaavoilla

regressioanalyysi Excelissä-perusteet

tilastollisessa mallinnuksessa regressioanalyysillä arvioidaan kahden tai useamman muuttujan välisiä suhteita:

riippuvainen muuttuja (aka criterion variable) on tärkein tekijä, jota yrität ymmärtää ja ennustaa.

riippumattomat muuttujat (eli selittävät muuttujat tai ennustajat) ovat tekijöitä, jotka saattavat vaikuttaa riippuvaiseen muuttujaan.

regressioanalyysi auttaa ymmärtämään, miten riippuvainen muuttuja muuttuu, kun yksi itsenäisistä muuttujista vaihtelee, ja sen avulla voidaan määrittää matemaattisesti, millä näistä muuttujista on oikeasti vaikutusta.

teknisesti regressioanalyysimalli perustuu neliöiden summaan, joka on matemaattinen tapa löytää datapisteiden hajonta. Mallin tavoitteena on saada mahdollisimman pieni neliösumma ja piirtää viiva, joka tulee lähimmäksi dataa.

tilastoissa ne erottavat toisistaan yksinkertaisen ja moninkertaisen lineaarisen regression. Yksinkertainen lineaarinen regressio mallintaa riippuvan muuttujan ja yhden riippumattoman muuttujan suhdetta lineaarisen funktion avulla. Jos käytät kahta tai useampaa selittävää muuttujaa riippuvan muuttujan ennustamiseen, käsittelet moninkertaista lineaarista regressiota. Jos riippuvainen muuttuja mallinnetaan epälineaarisena funktiona, koska datasuhteet eivät seuraa suoraa viivaa, käytä sen sijaan epälineaarista regressiota. Painopiste tämän opetusohjelman on yksinkertainen lineaarinen regressio.

otetaan esimerkiksi sateenvarjojen myyntiluvut 24 viime kuukauden ajalta ja selvitetään kuukauden keskimääräinen sademäärä samalta ajanjaksolta. Piirretään nämä tiedot kaavioon, ja regressiolinja osoittaa riippumattoman muuttujan (Sademäärä) ja riippuvaisen muuttujan (sateenvarjomyynti) välisen suhteen: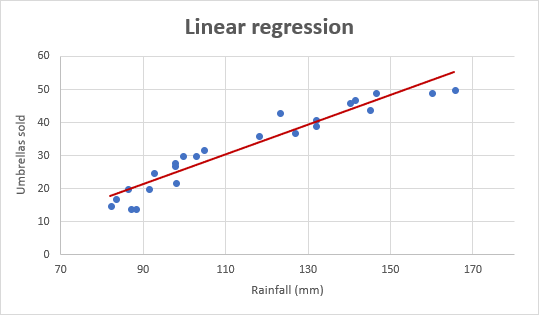

Lineaarinen regressioyhtälö

matemaattisesti lineaarinen regressio määritellään tällä yhtälöllä:

missä:

• x on itsenäinen muuttuja.
• y on riippuvainen muuttuja.
• a on Y-leikkauspiste, joka on Y: n odotettu keskiarvo, kun kaikki x: n muuttujat ovat yhtä kuin 0. Regressiokäyrässä se on piste, jossa Jana leikkaa Y-akselin.
• b on regressiolinjan kulmakerroin, joka on muutosnopeus y: lle x: n muuttuessa.
• ε on satunnaisvirhetermi, joka on riippuvan muuttujan todellisen arvon ja sen ennustetun arvon erotus.

lineaarisessa regressioyhtälössä on aina virhetermi, koska tosielämässä ennustajat eivät ole koskaan täysin tarkkoja. Jotkin ohjelmat, kuten Excel, tekevät kuitenkin virhetermin laskennan kulissien takana. Niinpä Excelissä tehdään lineaarinen regressio käyttäen pienimmän neliösumman menetelmää ja haetaan kertoimia A ja b siten, että:

esimerkissämme lineaarinen regressioyhtälö saa seuraavan muodon:

Umbrellas sold = b * rainfall + a

on olemassa kourallinen erilaisia tapoja löytää A ja B. kolme pääasiallista menetelmää lineaarisen regressioanalyysin suorittamiseksi Excelissä ovat:

• Regressiotyökalu mukana Analyysityökalupak
• Hajontakaavio trendiviivalla
• Lineaarinen regressiokaava

alla on yksityiskohtaiset ohjeet kunkin menetelmän käytöstä.

miten lineaarinen regressio tehdään Excelissä Analysis ToolPak

Tämä esimerkki näyttää, miten regressio suoritetaan Excelissä käyttämällä erityistä työkalua, joka sisältyy Analysis ToolPak-lisäosaan.

ota Analyysityökalupak-lisäosa käyttöön

Analyysityökalupak on saatavilla kaikissa Excel 2019-2003-versioissa, mutta se ei ole oletusarvoisesti käytössä. Joten, sinun täytyy kytkeä se manuaalisesti. Näin:

1. valitse Excelissä tiedosto > Options.
2. valitse Excel-asetukset-valintaikkunassa lisäosat vasemmasta sivupalkista, varmista, että Excel-lisäosat on valittu Hallitse-ruutuun ja napsauta Go.
   
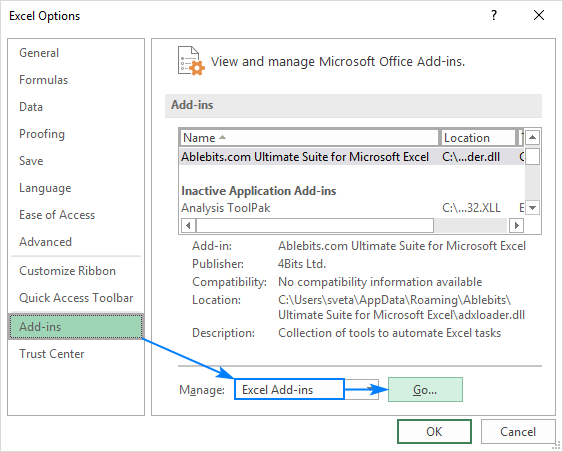
3. lisäosat-valintaikkunassa rasti pois Analyysityökalupakin ja klikkaa OK:
   

Tämä lisää data-analyysityökalut Excel-nauhan Data-välilehteen.

Suorita regressioanalyysi

tässä esimerkissä teemme yksinkertaisen lineaarisen regression Excelissä. Meillä on luettelo keskimääräisistä kuukausittaisista sademääristä viimeisten 24 kuukauden ajalta sarakkeessa B, joka on itsenäinen muuttujamme (ennustaja), ja myytyjen sateenvarjojen määrä sarakkeessa C, joka on riippuvainen muuttuja. Tietenkin on monia muitakin tekijöitä, jotka voivat vaikuttaa myyntiin, mutta nyt keskitymme vain näihin kahteen muuttujaan: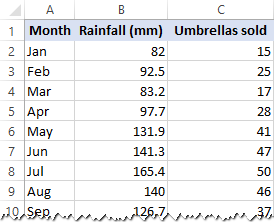

kun analyysityökalu on lisätty käyttöön, suorita nämä vaiheet regressioanalyysin suorittamiseksi Excelissä:

1. Data-välilehdellä, Analyysiryhmässä, klikkaa Data Analysis-painiketta.
   
2. valitse regressio ja napsauta OK.
   
3. määritä regressio-valintaikkunassa seuraavat asetukset:
   • valitse syöte y-alue, joka on riippuvainen muuttujastasi. Meidän tapauksessamme se on sateenvarjo myynti (C1: C25).
   • valitse tuloalue X, eli itsenäinen muuttuja. Tässä esimerkissä se on keskimääräinen kuukausittainen sademäärä (B1: B25).

   Jos rakennat moninkertaista regressiomallia, valitse kaksi tai useampia vierekkäisiä sarakkeita, joissa on erilaisia riippumattomia muuttujia.

   • Tarkista Nimilaatikosta, onko X-ja Y-alueittesi yläosassa otsikoita.
   • Valitse haluamasi tulostusvaihtoehto, uusi laskentataulukko meidän tapauksessamme.
   • valinnaisesti, valitse Residuals-valintaruutu saadaksesi erotuksen ennustettujen ja todellisten arvojen välillä.
     
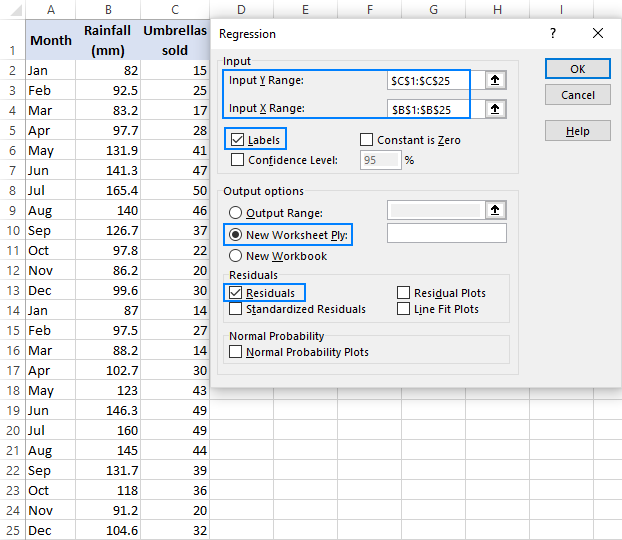
4. klikkaa OK ja tarkkaile Excelin luomaa regressioanalyysin tuotosta.

tulkitse regressioanalyysin lähtö

kuten juuri näit, regression suorittaminen Excelissä on helppoa, koska kaikki laskelmat muotoillaan automaattisesti. Tulosten tulkinta on hieman hankalampi, koska pitää tietää, mitä jokaisen numeron takana on. Alla on 4 pääosan erittely regressioanalyysin tuotoksesta.

regressioanalyysin tuotos: Yhteenveto

Tämä osa kertoo, kuinka hyvin laskettu lineaarinen regressioyhtälö sopii lähdeaineistoosi.

näin kukin tieto tarkoittaa:

moninkertainen R. korrelaatiokerroin mittaa kahden muuttujan välisen lineaarisen suhteen vahvuutta. Korrelaatiokerroin voi olla mikä tahansa arvo välillä -1 ja 1, ja sen itseisarvo ilmaisee suhteen vahvuuden. Mitä suurempi itseisarvo, sitä vahvempi suhde:

• 1 tarkoittaa vahvaa positiivista suhdetta
• -1 tarkoittaa vahvaa negatiivista suhdetta
• 0 tarkoittaa ei suhdetta lainkaan

neliö. Se on Determinaatiokerroin, jota käytetään sopivuuden indikaattorina. Se näyttää, kuinka monta pistettä putoaa regressiolinjalle. R2-arvo lasketaan neliöiden kokonaissummasta, tarkemmin se on alkuperäisten tietojen neliöllisten poikkeamien summa keskiarvosta.

esimerkissämme R2 on 0,91 (pyöristettynä 2-numeroihin), mikä on fairy good. Se tarkoittaa, että 91% arvoistamme sopii regressioanalyysimalliin. Toisin sanoen 91% riippuvaisista muuttujista (y-arvot) selitetään riippumattomilla muuttujilla (x-arvot). Yleensä R potenssiin 95% tai enemmän pidetään hyvä istuvuus.

oikaistu R neliö. Se on R-neliö, joka on mukautettu mallin riippumattoman muuttujan lukumäärälle. Haluat käyttää tätä arvoa R-neliön sijasta useita regressioanalyysejä varten.

keskivirhe. Se on toinen hyvyys-of-fit-mittari, joka osoittaa regressioanalyysin tarkkuuden-mitä pienempi luku, sitä varmempi voit olla regressioyhtälöstä. Siinä missä R2 edustaa mallin selittämää riippuvien muuttujien varianssin prosenttiosuutta, keskivirhe on absoluuttinen mitta, joka osoittaa datapisteiden keskimääräisen etäisyyden regressiolinjasta.

havaintoja. Kyse on yksinkertaisesti mallisi havaintojen määrästä.

regressioanalyysin tuotos: ANOVA

tuotoksen toinen osa on varianssin analyysi (Anova):

periaatteessa se jakaa neliöiden summan yksittäisiin komponentteihin, jotka antavat tietoa regressiomallisi vaihtelutasoista:

• df on varianssin lähteisiin liittyvien vapausasteiden lukumäärä.
• SS on neliöiden summa. Mitä pienempi SS: n jäännös verrattuna SS: ään, sitä paremmin mallisi sopii tietoihin.
• MS on keskimääräinen neliö.
• F on F-statisti eli nollahypoteesin F-testi. Sen avulla testataan mallin kokonaismerkitystä.
• merkitys F on F: n P-arvo.

Anova-osaa käytetään harvoin yksinkertaiseen lineaariseen regressioanalyysiin Excelissä, mutta viimeistä komponenttia kannattaa ehdottomasti katsoa tarkkaan. Merkitsevyys F-arvo antaa käsityksen siitä, kuinka luotettavia (tilastollisesti merkittäviä) tuloksesi ovat. Jos merkitys F on alle 0,05 (5%), mallisi on OK. Jos se on suurempi kuin 0,05, sinun on luultavasti parempi valita toinen riippumaton muuttuja.

regressioanalyysin tuotos: kertoimet

Tämä osio antaa tarkempaa tietoa analyysisi komponenteista:

tässä osiossa hyödyllisin komponentti on kertoimet. Sen avulla voit rakentaa lineaarisen regressioyhtälön Exceliin:

tietokokonaisuudellemme, jossa y on myytyjen sateenvarjojen lukumäärä ja x keskimääräinen kuukausittainen sademäärä, lineaarinen regressiokaavamme menee seuraavasti:

Y = Rainfall Coefficient * x + Intercept

varustettu a – ja B-arvoilla pyöristettynä kolmeen desimaaliin, se muuttuu:

Y=0.45*x-19.074

esimerkiksi, kun kuukauden keskimääräinen sademäärä on 82 mm, sateenvarjomyynti olisi noin 17,8:

0.45*82-19.074=17.8

vastaavalla tavalla, voit selvittää kuinka monta sateenvarjoa aiotaan myydä muiden määrittämiesi kuukausisateiden (x muuttuja) kanssa.

regressioanalyysin tuotos: jäännöksiä

jos verrataan myytyjen sateenvarjojen arvioitua ja todellista määrää, joka vastaa 82 mm: n kuukausisadetta, nämä luvut ovat hieman erilaiset:

• arvioitu: 17.8 (laskettu edellä)
• todellinen: 15 (lähdeaineiston rivi 2)

miksi ero? Koska riippumattomat muuttujat eivät koskaan ole täydellisiä ennustajia riippuvaisille muuttujille. Ja jäännökset voivat auttaa sinua ymmärtämään, kuinka kaukana todelliset arvot ovat ennustetuista arvoista:

miten tehdä Lineaarinen regressiokäyrä Excelissä

Jos haluat nopeasti visualisoida kahden muuttujan välisen suhteen, piirrä lineaarinen regressiokaavio. Se on hyvin helppoa! Näin:

1. Valitse kaksi saraketta, joissa on tietosi, mukaan lukien otsikot.
2. pikkukuva-välilehdellä, chatit-ryhmässä, klikkaa Scatter-kaavion kuvaketta ja valitse Scatter-pikkukuva (ensimmäinen):
   

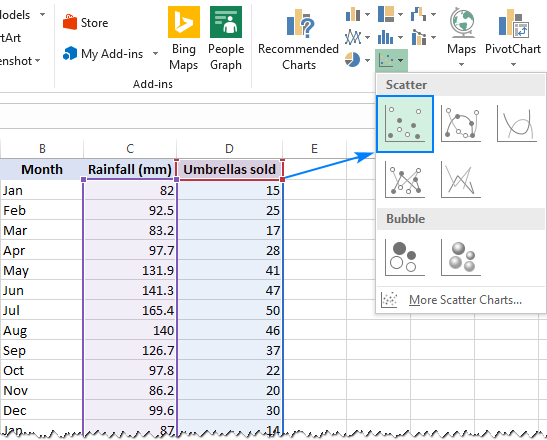
   Tämä lisää scatter-kuvaajan laskentataulukkoosi, joka muistuttaa tätä:
   

3. nyt on piirrettävä vähiten neliöt regressiolinja. Jos haluat tehdä sen, napsauta hiiren oikealla painikkeella mitä tahansa kohtaa ja valitse Lisää Trendline… kontekstivalikosta.
   
4. oikeassa ruudussa, valitse Lineaarinen trendilinjan muoto ja vaihtoehtoisesti tarkista näytön yhtälö kaaviosta saadaksesi regressiokaavan:
   

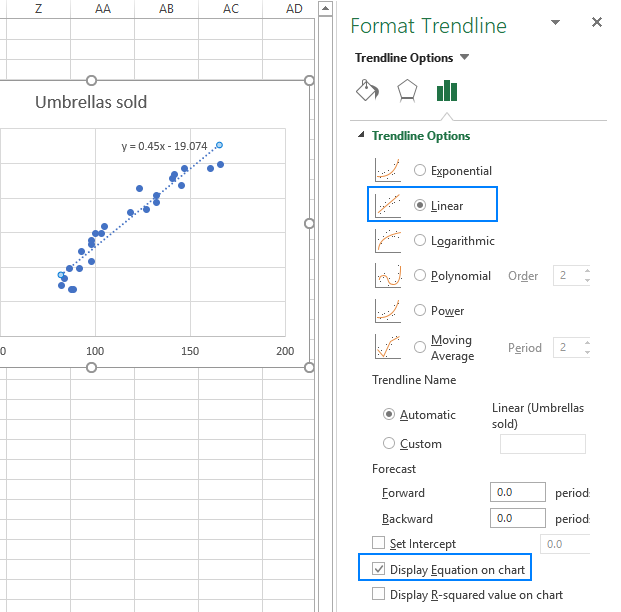
   kuten saatat huomata, Excelin meille luoma regressioyhtälö on sama kuin kertoimien lähtöihin perustuva lineaarinen regressiokaava.

5. Vaihda täytön & rivi-välilehteen ja mukauta rivi mieleiseksesi. Voit esimerkiksi valita eri viivan värin ja käyttää umpiviivaa dashed-viivan sijaan (valitse Viivatyyppisestä ruudusta kiinteä viiva):
   

tässä vaiheessa kaaviosi näyttää jo kunnon regressiografialta:

• vedä yhtälö sinne minne parhaaksi näet.
• lisää akselien otsikot (kaavion elementit-painike > akselien otsikot).
• Jos datapisteesi alkavat vaaka-ja / tai pystyakselin keskeltä, kuten tässä esimerkissä, haluat ehkä päästä eroon liiallisesta valkoisesta tilasta. Seuraavassa vinkissä selitetään, miten tämä tehdään: skaalaa karttaakselit pienentämään valkoista tilaa.

  ja Tältä näyttää meidän parannettu regressiokäyrä:
  

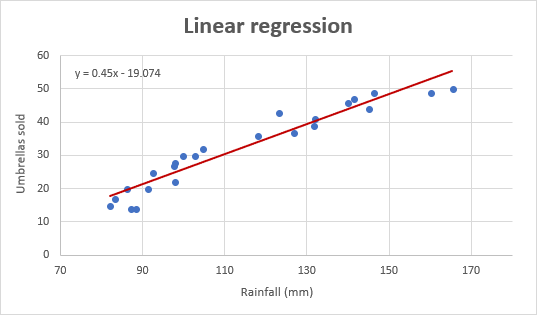  Tärkeä huomautus! Regressiokäyrässä itsenäisen muuttujan tulee aina olla X-akselilla ja riippuvan muuttujan Y-akselilla. Jos kuvaaja on piirretty päinvastaisessa järjestyksessä, vaihda sarakkeet laskentataulukossa ja piirrä sitten kaavio uudelleen. Jos et saa järjestää lähdetietoja uudelleen, voit vaihtaa X-ja Y-akselit suoraan kaaviossa.

miten regressio tehdään Excelissä käyttäen kaavoja

Microsoft Excelissä on muutamia tilastollisia funktioita, joiden avulla voit tehdä lineaarisen regressioanalyysin, kuten LINEST, SLOPE, INTERPET ja CORREL.

LINEST-funktio laskee pienimmän neliösumman regressiomenetelmällä suoran, joka parhaiten selittää muuttujien välisen suhteen, ja palauttaa rivin, joka kuvaa kyseistä suoraa. Löydät yksityiskohtaisen selityksen toiminnon syntaksi tässä opetusohjelma. Nyt tehdään vain kaava otosaineistollemme:

=LINEST(C2:C25, B2:B25)

koska LINEST-funktio palauttaa joukon arvoja, se on syötettävä array-kaavana. Valitse kaksi vierekkäistä solua samalla rivillä, E2:F2 meidän tapauksessamme, kirjoita kaava, ja paina Ctrl + Shift + Enter täydentää sitä.

kaava palauttaa b-kertoimen (E1) ja A-vakion (F1) jo tutulle lineaariselle regressioyhtälölle:

y = bx + a

Jos et käytä taulukkokaavoja laskentataulukoissa, voit laskea a: n ja B: n erikseen säännöllisillä kaavoilla:

get the y-intercept (a):

=INTERCEPT(C2:C25, B2:B25)

get the slope (B):

=SLOPE(C2:C25, B2:B25)

lisäksi löytyy korrelaatiokerroin (regressioanalyysin yhteenvetotuloksesta moninkertainen R), joka kertoo kuinka voimakkaasti nämä kaksi muuttujaa liittyvät toisiinsa:

=CORREL(B2:B25,C2:C25)

seuraava kuvakaappaus näyttää kaikki nämä Excel-regressiokaavat toiminnassa:

näin tehdään lineaarinen regressio Excelissä. Se sanoi, pidä mielessä, että Microsoft Excel ei ole tilasto-ohjelma. Jos haluat suorittaa regressioanalyysin ammattilaistasolla, voit käyttää kohdennettuja ohjelmistoja, kuten XLSTAT, RegressIt jne.

saatavilla olevat lataukset:

katsoaksesi tarkemmin lineaarisia regressiokaavojamme ja muita tekniikoita, joita tässä opetusohjelmassa käsitellään, voit ladata näytteen Regressioanalyysimme Excel-työkirjasta.

• miten käytetään ratkaisijaa Excelissä esimerkein
• miten lasketaan Koronkorko Excelissä
• Miten lasketaan CAGR (compound annual growth rate) Excelissä