liikemäärän säilyminen on fysiikan peruskäsite energian ja massan säilymisen kanssa.Liikemäärä määritellään kappaleen massaksi kerrottuna kappaleen nopeudella.Liikemäärän säilymisessä todetaan, että jonkin ongelmakohdan sisällä liikemäärän määrä pysyy vakiona;liikemäärä ei synny eikä tuhoudu, vaan muuttuu vain Newtonin liikelakien kuvaamien voimien vaikutuksesta.Liikemäärän käsitteleminen on vaikeampaa kuin massan ja energian käsittely, koska Momentum on avektorikiintiö, jolla on sekä Suure että suunta. Liikemäärä säilyy kaikissa kolmessa fyysisessä suunnassa yhtä aikaa. Se on vielä vaikeampaa käsiteltäessä agasbecause voimat yhteen suuntaan voivat vaikuttaa vauhtia toiseen suuntaansyynä törmäykset monien molekyylien.Tällä liukumäellä esitämme hyvin, hyvin yksinkertaistetun virtausongelman, jossa ominaisuudet muuttuvat vain yhteen suuntaan.Ongelmaa yksinkertaistetaan edelleen tarkastelemalla tasaista virtausta, joka ei muutu ajan myötä, ja rajoittamalla voimat vain niihin, jotka ovat yhteydessä thepressure.Be tiedostavat, että todelliset virtausongelmat ovat paljon monimutkaisempia kuin tämä yksinkertainen esimerkki.

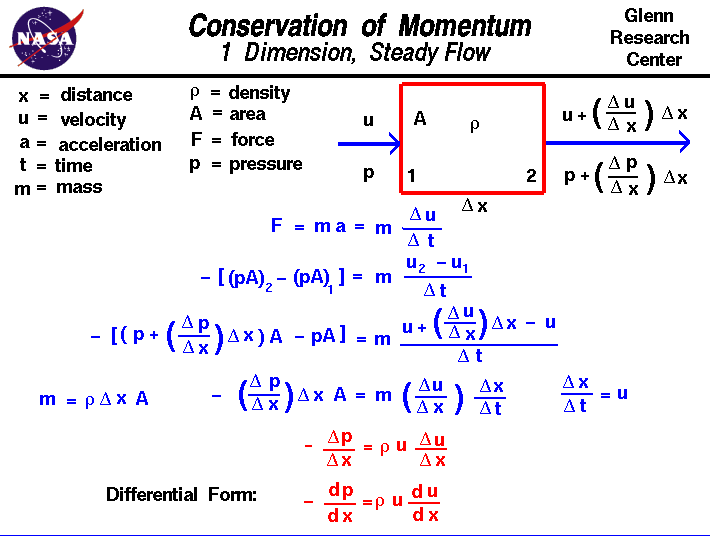
Tarkastellaanpa kaasun virtausta sellaisen alueen läpi, jossa virtaus muuttuu vain yhteen suuntaan, jota kutsumme ”x”: ksi. Kaasu tulee domainatin asemalle 1 jonkin verran nopeudella u ja jonkin verran painepand poistuu asemalta 2 eri nopeudella ja paineella. Yksinkertaisuuden vuoksi oletamme, että tiheys r pysyy muuttumattomana alueella ja että alue A, jonka läpi kaasu virtaa, pysyy myös muuttumattomana. Asemien 1 ja 2 sijainti on erotettu del x: ksi kutsutulla etäisyydellä (Delta on pieni kolmio slideand on Kreikan kirjain ”d”. Matemaatikot käyttävät usein tätä symbolia ilmaisemaan jonkin suureenmuutoksen tai muunnelman. Web print-fontti ei tue kreikkalaisia kirjaimia, joten kutsumme sitä vain ”del”.) Muutosta etäisyyden kanssa kutsutaan kaltevuudeksi, jotta vältetään sekaannus ajan kanssa tapahtuvaan muutokseen, jota kutsutaan nopeudeksi.Nopeusgradientti on merkitty del u / del x; muutos nopeus per muutos etäisyys. Joten asemalla 2 nopeus saadaan nopeudesta 1 plus gradientti kertaa etäisyys.

samanlainen lauseke antaa paineelle poistumisen:

Kappaleelle, jonka massa on vakio, tämä pelkistyy massa-kertaiseksi kiihtyvyydeksi a.An kiihtyvyys on nopeuden muutos, johon liittyy ajan muutos (del u / del t). Sitten:

tämän problematiikan voima johtuu painegradientista. Koska paine on voima pinta-alayksikköä kohti,nettovoima meidän fluid domain on paine kertaa alueen theexit miinus paine kertaa alueen suulla.

tämän lausekkeen alussa olevaa miinusmerkkiä käytetään, koska kaasut siirtyvät korkeapaineen alueelta matalapaineen alueelle; jos paine kasvaa X: n kanssa, nopeus pienenee. Korvaavat lausekkeet nopeudelle ja paineelle:

Simplify:

toteaa, että (del x / del t) on thevelocity ja että massa on tiheys r kertaa tilavuus (pinta – ala kertaa del x):

simplify:

del P / del x Ja del u / del x edustavat paineen ja nopeuden gradientteja.Jos kutistamme verkkotunnuksemme differentiaalikokoihin, nämä gradientit muuttuvat differentiaaleiksi:

Tämä on yksiulotteinen, tasainen muoto Eulerin Equation.It on mielenkiintoista huomata, että painehäviö fluidin (termi vasemmalla) on verrannollinen sekä arvo thevelocity ja kaltevuus nopeus.A ratkaisu tämän momentum yhtälö antaa meille muodossa thedynamic paine, joka näkyy bernoullin yhtälö.

toiminta:
Opastetut kierrokset

• Basic Fluid Dynamics Equations:

navigointi ..

aloittelijan oppaan Kotisivu