MathHelp.com

eli jos datapiste on alle Q1 – 1,5×IQR tai yli Q3 + 1,5×IQR, sen katsotaan olevan liian kaukana keskeisistä arvoista ollakseen kohtuullinen. Ehkä törmäsit punnitukseen, kun teit sitä yhtä mittausta, tai ehkä työparisi on idiootti, eikä sinun olisi pitänyt antaa hänen koskea laitteisiin. Kuka tietää? Mutta oli niiden syy mikä tahansa, outlaiers ovat niitä kohtia, jotka eivät näytä ”sovi”.

kun olet tyytyväinen IQR: n löytämiseen, voit siirtyä paikantamaan mahdolliset poikkeamat.

• Etsi mahdolliset poikkeamat seuraavasta tietojoukosta:

pitoisuus jatkuu

arvot Q1 – 1.5×IQR ja Q3 + 1.5×IQR ovat ”aidat”, jotka merkitsevät” kohtuulliset ” arvot outlier-arvoista. Aitojen ulkopuolella lojuu vieraslajeja.

jos tehtävänantosi on se, että otat huomioon poikkeavien arvojen lisäksi myös ”ääriarvot”, arvot Q1 – 1.5×IQR ja Q3 + 1.5×IQR ovat ”sisemmät” aidat ja arvot Q1 – 3×IQR ja Q3 + 3×IQR ovat ”ulommat” aidat.

ulkoaidat (merkitty tähdellä tai avoimilla pisteillä) ovat sisä-ja ulkoaitojen välissä, ja ääriarvot (merkitty kummalla symbolilla, jota et käyttänyt ulkoaitojen kohdalla) ovat ulkoaitojen ulkopuolella.

muuten kirjasi voi viitata arvon ”1,5×IQR” olevan ”askel”. Tällöin outlierit ovat numeroita, jotka ovat yhden ja kahden askeleen päässä saranoista, ja ääriarvot ovat numeroita, jotka ovat yli kahden askeleen päässä saranoista.

kun katsotaan vielä edellistä esimerkkiä, ulkoaidat olisivat lukemissa 14,4 – 3×0,5 = 12,9 ja 14,9 + 3×0,5 = 16,4. Koska 16,4 on aivan ulkoratojen yläpäässä, tätä pidettäisiin vain ulkoratojen ulkopuolisena arvona, ei äärimmäisenä arvona. 10,2 on kuitenkin täysin alemman ulkoaidan alapuolella, joten 10,2 olisi ääriarvo.

grafiikkalaskurisi voi ilmoittaa, sisältääkö lokero-ja viiksijuoni poikkeamia. Esimerkiksi edellä mainittu ongelma sisältää kohdat 10.2, 15.9 ja 16.4 poikkeavina. Yksi asetus graafilaskurissani antaa yksinkertaisen laatikko-ja viiksikäyrän, joka käyttää vain viisinumeroista summaa, joten kauimmaiset poikkeamat esitetään viiksien päätepisteinä:

eri laskinasetuksella saadaan laatikko-ja viiksikäyrä, jossa poikkeamat on erityisesti merkitty (tässä tapauksessa avoimen pisteen simulaatiolla), ja viikset menevät vain korkeimpiin ja pienimpiin arvoihin, jotka eivät ole poikkeavia:

laskurini ei tee eroa poikkeavien ja ääriarvojen välillä. Ei ehkä sinunkaan. Tarkista omistajan käsikirja nyt, ennen seuraavaa testiä.

Jos käytät graafilaskinta apuna näissä tonteissa, varmista, että tiedät, mitä asetusta sinun pitäisi käyttää ja mitä tulokset tarkoittavat, tai laskin voi antaa sinulle täysin oikean, mutta ”väärän” vastauksen.

• Etsi mahdolliset poikkeamat ja ääriarvot seuraavasta tietojoukosta ja piirrä laatikko-ja viiksijuoni. Merkitse mahdolliset poikkeamat tähdellä ja ääriarvot avoimella pisteellä.

Mainos

löytääkseni poikkeamat ja ääriarvot minun on ensin löydettävä IQR. Koska luettelossa on seitsemän arvoa, mediaani on neljäs arvo, joten:

Q2 = 25

listan alkupuoli on:

21, 23, 24

…niin Q1 = 23; jälkipuolisko on:

29, 33, 49

…siis Q3 = 33. Sitten IQR annetaan:

IQR = 33 – 23 = 10

poikkeamat ovat mitä tahansa alla olevia arvoja:

23 – 1.5×10 = 23 – 15 = 8

…tai yli:

33 + 1.5×10 = 33 + 15 = 48

ääriarvot ovat seuraavat:

23 – 3×10 = 23 – 30 = -7

…tai yli:

33 + 3×10 = 33 + 30 = 63

joten minulla on outlier 49, mutta ei ääriarvoja. Huippuviisikkoa tontilleni ei tule, sillä Q3 on myös korkein ei-outlier. Juoneni näyttää tältä.:

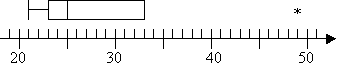
on huomattava, että edellä esitetyt menetelmät, termit ja säännöt ovat sitä, mitä olen opettanut ja mitä olen yleisimmin nähnyt opetetun. Kurssillasi voi kuitenkin olla erilaisia erityissääntöjä, tai laskimesi voi tehdä laskutoimituksia hieman eri tavalla. Sinun on ehkä hieman joustettava opetussuunnitelmaasi liittyvien vastausten löytämisessä.