kompleksiluvut: introduction (sivu 1/3)

sections: Introduction, operations with complexes, the quadratic kaava

tähän asti on sanottu, ettei negatiivisen luvun neliöjuurta voi ottaa. Tämä johtuu siitä, sinulla ei ollut numeroita, jotka olivat negatiivisia, kun olit potenssiin ne (joten et voinut ”mennä taaksepäin” ottamalla neliöjuuri). Jokainen numero oli positiivinen. Joten et voinut oikein neliöjuurta negatiivista ja odottaa keksiväsi mitään järkevää.

nyt voidaan kuitenkin ottaa negatiivisen luvun neliöjuuri, mutta siihen tarvitaan uuden luvun käyttäminen. Tämä uusi numero keksittiin(löydetty?) uskonpuhdistuksen aikoihin. Tuohon aikaan kukaan ei uskonut, että tälle uudelle luvulle löytyisi mitään ”reaalimaailman” käyttöä, muuta kuin tiettyjen yhtälöiden ratkaisemiseen liittyvien laskutoimitusten helpottamista, joten uutta lukua pidettiin mukavuussyistä keksittynä teeskentelylukuna.

(mutta sitten kun asiaa ajattelee, eivätkö kaikki numerot ole keksintöjä? Numerot eivät kasva puissa! He elävät päässämme. Keksimme ne kaikki! Miksemme keksisi uutta, kunhan se toimii hyvin sen kanssa, mitä meillä jo on?)

Then:

nyt voi luulla, että näin voi tehdä:

, mutta tässä ei ole mitään järkeä! Sinulla on jo kaksi numeroa, jotka neliö on 1; nimittäin -1 ja +1. Ruutulukema on jo -1. Joten se ei ole järkevää, että olisin myös neliön 1. Tämä osoittaa tärkeän yksityiskohdan: Kun käsittelet mielikuvitusta, saat jotain (kyky käsitellä negatiivisia sisällä neliön juuret), mutta menetät myös jotain (joitakin joustavuutta ja kätevä sääntöjä sinulla oli käsitellessäsi neliön juuret). Erityisesti sinun täytyy aina tehdä i-osa ensin!

• yksinkertaistaa sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Kaikki oikeudet pidätetään

(Varoitus: kolmannen ”equals” – merkin läpi kulkeva askel on ” ”, ei ””. Minä on radikaalin ulkopuolella.)

• yksinkertaistaa sqrt(-25).

laskelmissasi käsittelet i: tä aivan kuten X: ää, paitsi että x2 on vain x2, mutta i2 on -1:

• yksinkertaistaa 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• yksinkertaistaa 16I – 5I.

16i – 5i = (16 – 5)i = 11i

• kerrotaan ja yksinkertaistetaan (3i)(4i).

(3i)(4i) = (3·4)(i·i) = (12) (i2) = (12)(-1) = -12

• kerrotaan ja yksinkertaistetaan(i) (2i) (–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6I

Huomaa Tämä viimeinen ongelma. Sen sisällä voi nähdä, että , koska i2 = -1. Jatketaan, saamme:

tämä potenssien, merkkien, 1: n ja i: n malli on sykli:

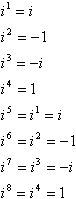
toisin sanoen I: n suuren potenssin laskemiseksi sen voi muuntaa pienemmäksi potenssiksi kun otetaan lähin kerrannainen 4, joka ei ole suurempi kuin eksponentti ja vähennetään tämä kerrannainen eksponentista. Esimerkiksi yleinen kompakysymys testeissä on jotain tyyliin ”Simplify i99”, ajatuksena on, että yrität moninkertaistaa i yhdeksänkymmentäyhdeksän kertaa ja sinulta loppuu aika, ja opettajat saavat hyvän kikatuksen kustannuksellasi tiedekunnan loungessa. Näin oikotie toimii:

i99 = i96+3 = i(4×24)+3 = i3 = –i

eli i99 = i3, koska I96: sta voi vain lohkaista irti. (Yhdeksänkymmentäkuusi on neljän kerrannainen, joten i96 on vain 1, jonka voi sivuuttaa.) Toisin sanoen, voit jakaa eksponentti 4 (käyttäen pitkä jako), hylkää vastaus, ja käyttää vain loput. Tämä antaa sinulle sen osan eksponentista, josta välität. Tässä muutama muu esimerkki:

• yksinkertaistaa i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>