antakaa pilkulla erotellut luvut laskemiseksi.

Related Statistics Calculator/Standard Deviation Calculator / Sample Size Calculator

Mean

sana mean, joka on homonyymi useille muille sanoille englannin kielessä, on vastaavasti epäselvä myös matematiikan alalla. Asiayhteydestä riippuen, olivatpa ne matemaattisia tai tilastollisia, mitä” mean ” – muutoksilla tarkoitetaan. Yksinkertaisimmassa matemaattisessa määritelmässään tietojoukoista käytetty keskiarvo on aritmeettinen keskiarvo, jota kutsutaan myös matemaattiseksi odotukseksi eli keskiarvoksi. Tässä muodossa keskiarvo tarkoittaa diskreetin lukujoukon väliarvoa eli tietojoukon kaikkien arvojen summaa jaettuna arvojen kokonaismäärällä. Aritmeettisen keskiarvon laskemisessa käytettävä yhtälö on käytännössä sama kuin tilastollisten perusjoukon ja otoksen keskiarvon käsitteiden laskemisessa, ja käytetyt muuttujat vaihtelevat hieman:

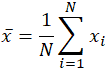
keskiarvoa merkitään usein x: llä, joka lausutaan ”x bar”, ja muissakin käyttötarkoituksissa, joissa muuttuja ei ole x, bar-notaatio on yleinen indikaattori jonkinlaisesta keskiarvosta. Erityistapauksessa perusjoukon keskiarvosta käytetään muuttujan x sijasta kreikkalaista tunnusta mu eli μ. Vastaavasti, tai pikemminkin hämmentävästi, otoskeskiarvo ilmoitetaan tilastoissa usein Isolla X: llä. Koska tietoaineisto 10, 2, 38, 23, 38, 23, 21, edellä esitetyn tuotosten yhteenlaskun soveltaminen:

kuten aiemmin mainittiin, tämä on yksi yksinkertaisimmista keskiarvon määritelmistä, ja joitakin muita ovat painotettu aritmeettinen keskiarvo (joka eroaa vain siinä, että tietojoukon tietyt arvot antavat enemmän arvoa kuin toiset) sekä geometrinen keskiarvo. Tiettyjen tilanteiden ja asiayhteyksien asianmukainen ymmärtäminen voi usein antaa henkilölle tarvittavat välineet sen määrittämiseksi, mitä tilastollisesti relevanttia menetelmää tulee käyttää. Yleisesti ottaen keskiarvo, mediaani, moodi ja vaihteluväli olisi ihanteellisesti laskettava ja analysoitava tietyn näytteen tai tietojoukon osalta, koska ne valaisevat tietyn datan eri näkökohtia ja voivat yksinään tarkasteltuna johtaa tietojen vääriin tulkintoihin, kuten seuraavissa kohdissa osoitetaan.

mediaani

tilastollinen käsite mediaani on arvo, joka jakaa aineiston otoksen, perusjoukon tai todennäköisyysjakauman kahteen puolikkaaseen. Mediaanin löytämiseen liittyy olennaisesti arvon löytäminen datanäytteestä, jolla on fyysinen sijainti muiden lukujen välissä. Huomaa, että äärellisen lukuluettelon mediaania laskettaessa datanäytteiden järjestys on tärkeä. Perinteisesti arvot on lueteltu nousevassa järjestyksessä, mutta ei ole mitään todellista syytä, että arvojen listaaminen laskevassa järjestyksessä tuottaisi erilaisia tuloksia. Jos dataotoksen arvojen kokonaismäärä on pariton, mediaani on yksinkertaisesti kaikkien arvojen luettelon keskellä oleva luku. Kun aineistonäyte sisältää parillisen määrän arvoja, mediaani on kahden keskimmäisen arvon keskiarvo. Vaikka tämä voi olla hämmentävää, muista vain, että vaikka mediaaniin joskus liittyy keskiarvon laskeminen, kun tämä tapaus syntyy, siihen liittyy vain kaksi keskimmäistä arvoa, kun taas keskiarvoon kuuluvat kaikki datanäytteen arvot. Parittomissa tapauksissa, joissa on vain kaksi datanäytettä tai on parillinen määrä näytteitä, joissa kaikki arvot ovat samat, keskiarvo ja mediaani ovat samat. Kun otetaan huomioon sama tietokokonaisuus kuin ennenkin, mediaani saadaan seuraavalla tavalla:

2,10,21,23,23,38,38

kun tiedot on lueteltu nousevassa järjestyksessä ja kun on päätetty, että arvoja on pariton määrä, on selvää, että 23 on mediaani tässä tapauksessa. Jos tietoaineistoon olisi lisätty muuta lisäarvoa:

2,10,21,23,23,38,38,1027892

koska arvoja on parillinen määrä, mediaani on kahden keskimmäisen luvun, tässä tapauksessa 23 ja 23, keskiarvo, jonka keskiarvo on 23. On huomattava, että tässä nimenomaisessa tietoaineistossa poikkeavan arvon (arvon, joka on selvästi odotetun arvoalueen ulkopuolella), arvon 1,027,892, lisäämisellä ei ole todellista vaikutusta tietoaineistoon. Jos kuitenkin lasketaan keskiarvo tälle tietojoukolle, tulos on 128,505. 875. Tämä arvo ei selvästikään kuvaa hyvin tietoaineiston seitsemää muuta arvoa, jotka ovat paljon pienempiä ja arvoltaan lähempänä keskiarvoa ja poikkeavaa arvoa. Tämä on tärkein etu, kun käytetään mediaania tilastotiedon kuvaamisessa keskiarvoon verrattuna. Vaikka sekä molemmat että muut tilastolliset arvot olisi laskettava tietoja kuvattaessa, jos vain yhtä voidaan käyttää, mediaani voi antaa paremman arvion tietyn tietojoukon tyypillisestä arvosta, kun arvojen välillä on erittäin suuria eroja.

moodi

tilastoissa moodi on tietojoukon arvo, jolla on eniten toistoja. Tietoaineisto voi olla multimodaalinen, mikä tarkoittaa, että siinä on useampi kuin yksi muoto. Esimerkiksi:

2,10,21,23,23,38,38

sekä 23 että 38 esiintyvät kumpikin kahdesti, joten ne molemmat ovat yllä olevan tietoaineiston moodi.

keskiarvon ja mediaanin tapaan moodia käytetään ilmaisemaan tietoa satunnaismuuttujista ja populaatioista. Toisin kuin keskiarvo ja mediaani, moodi on kuitenkin käsite, jota voidaan soveltaa ei-numeerisiin arvoihin, kuten yleisimmin ruokakaupasta ostettujen tortillalastujen merkkiin. Esimerkiksi, kun verrataan tuotemerkkejä Tostitos, Mission ja XOCHiTL, jos todetaan, että tortilla-sirujen myynnissä XOCHiTL on tila ja myy 3:2:1 suhteessa verrattuna Tostitos-ja Mission-merkkisiin tortilla-siruihin, suhdetta voidaan käyttää määrittämään, kuinka monta pussia kustakin merkistä on varastossa. Siinä tapauksessa, että 24 pussia tortilla pelimerkkejä myydä tiettynä aikana, myymälä olisi varastossa 12 pussia XOCHiTL pelimerkkejä, 8 Tostitos, ja 4 Mission jos käytät tilassa. Jos kuitenkin myymälä yksinkertaisesti käyttää keskimäärin ja myydään 8 pussia kutakin, se voisi mahdollisesti menettää 4 myynti, Jos asiakas halusi vain XOCHiTL pelimerkkejä eikä mitään muuta merkkiä. Kuten tästä esimerkistä käy ilmi, on tärkeää ottaa huomioon kaikki tilastollisten arvojen tavat, kun yritetään tehdä johtopäätöksiä mistä tahansa datanäytteestä.

vaihteluväli

tilastoaineiston vaihteluväli on suurimman ja pienimmän arvon erotus. Vaikka vaihteluvälillä on erilaisia merkityksiä tilastojen ja matematiikan eri alueilla, tämä on sen perusmääritelmä, ja sitä käytetään tarjotussa laskimessa. Samaa esimerkkiä käyttäen:

2,10,21,23,23,38,38
38 – 2 = 36

tässä esimerkissä vaihteluväli on 36. Keskiarvon tavoin vaihteluväliin voivat vaikuttaa merkittävästi erittäin suuret tai pienet arvot. Käyttäen samaa esimerkkiä kuin aiemmin: