matematiikka on enemmän maratonia kuin sprinttiä — se on pitkää, hidasta ja tasaista jauhamista, jossa on harvinaisia läpimurron hetkiä. Silti, silloin tällöin, saamme ne arvostetut ”Heureka” hetket, ne lyhyet kirjaimet ja numerot, jotka muuttavat tieteen ikuisesti. Tässä on joitakin kuuluisimpia yhtälöitä antiikin kreikkalaisista nykyaikaiseen fysiikkaan.

Pythagoran lause (530 eaa.)

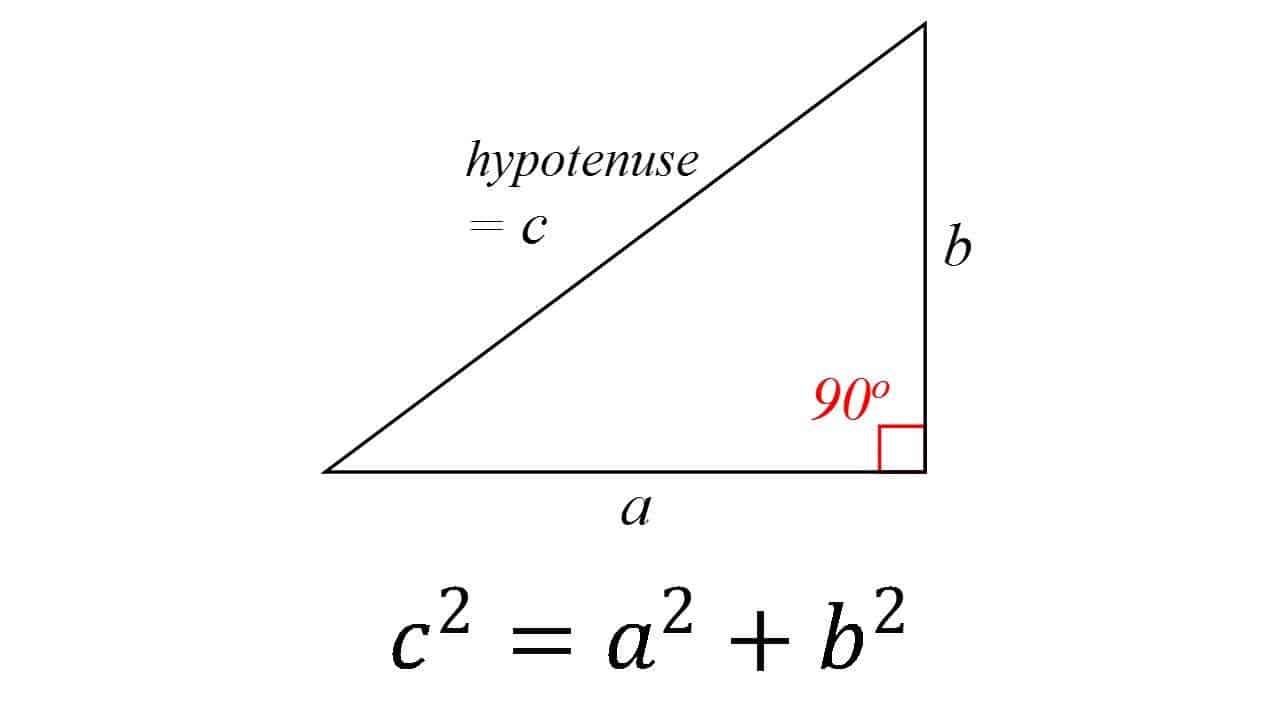
Tämä on nätti yksi perustavista pilareista kaikki geometria: suorakulmaisessa kolmiossa hypotenuusan neliö (suorakulmaisen kulman vastakohta) on yhtä suuri kuin kahden muun neliön summa. Teoriaa pidetään yleisesti kreikkalaisen matemaatikon Pythagoraan aikaansaannoksena, vaikka on jonkin verran todisteita siitä, että babylonialaiset matemaatikot ymmärsivät kaavan. On myös hyvin mahdollista, että lause oli tiedossa monet ihmiset, mutta hän oli ensimmäinen, joka todisti sen.

lauseelle on esitetty lukuisia todistuksia — mahdollisesti eniten mille tahansa matemaattiselle lauseelle. Ne ovat hyvin erilaisia, mukaan lukien sekä geometrisia vedoksia ja algebrallinen vedoksia, joista jotkut vuodelta tuhansia vuosia.

kompleksiluvut

italialainen matemaatikko Gerolamo Cardano on tiettävästi ensimmäinen, joka on ottanut käyttöön kompleksiluvut kutsuen niitä tuolloin ”kuvitteellisiksi”. ”I”: n matemaattinen kehitys neliöjuurta -1 edustavana imaginaarilukuna on kuitenkin laskettu Leonhard Eulerin ansioksi, joka oli yksi ihmiskunnan historian tärkeimmistä matemaatikoista ja tiedemiehistä.

kompleksiluvut ovat periaatteessa lukuja, joita ei oikeasti ole olemassa, mutta jotka ovat erittäin hyödyllisiä useissa laskelmissa. Ne koostuvat numerot todellinen osa (numerot me kaikki tiedämme) ja kuvitteellinen osa (I edustanut tässä) ja on käytännön sovelluksia monilla aloilla, mukaan lukien fysiikka, kemia, biologia, taloustiede, sähkötekniikka, ja tilastot.

logaritmit

logaritmit ovat käytännössä eksponentaation käänteisfunktio. Tarvitset luvun (N), emäksen (A), ja n: n logaritmi emäksessä A on x, jossa N vastaa A: n potenssia x. se voi tuntua vain erilaiselta tavaltä kirjoittaa sama asia (ja tavallaan se onkin), mutta logaritmeilla on lukemattomia käytännön sovelluksia, joita käytetään psykologiassa, taloudessa ja monien fysikaalisten ilmiöiden mittauksissa (kuten pH tai maanjäristyksen magnitudi).

logaritmit esitti julkisesti John Napier vuonna 1614 kirjassaan Mirifici Logarithmorum Canonis Descriptio (kuvaus logaritmien ihmeellisestä säännöstä) — osuva otsikko. Logaritmin erikoistapaus on luonnollinen logaritmi — e, jossa e on irrationaalinen ja Transsendenttiluku suunnilleen yhtä suuri kuin 2,71828182845. Itse asiassa, e itsessään on kiehtova historia ja vaikuttava määrä sovelluksia, mutta se on tarina toiseen aikaan.

Calculus

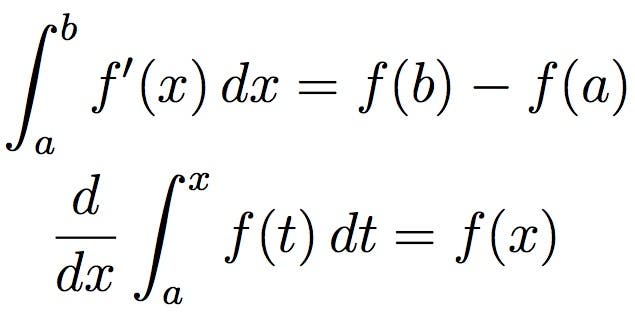
harvat matematiikan alat ovat olleet yhtä vaikuttavia kuin calculus. Isaac Newtonin ja Gottfried Wilhelm Leibnizin 1600-luvulla kehittämä calculus on laajalti käytössä tieteessä, tekniikassa ja taloustieteessä. Calculus keskittyy yleensä käsittelemään pieniä määriä, erityisesti äärettömän pieniä määriä. Laskennan kautta näitä voidaan käsitellä reaalilukuina, vaikka ne ovat teknisesti äärettömän pieniä.

yksinkertaisemmassa visualisoinnissa edellä kuvattua integraatiota voidaan ajatella funktion määrittelemän käyrän alle jäävän alueen mittaamisena.

Painovoimalaki

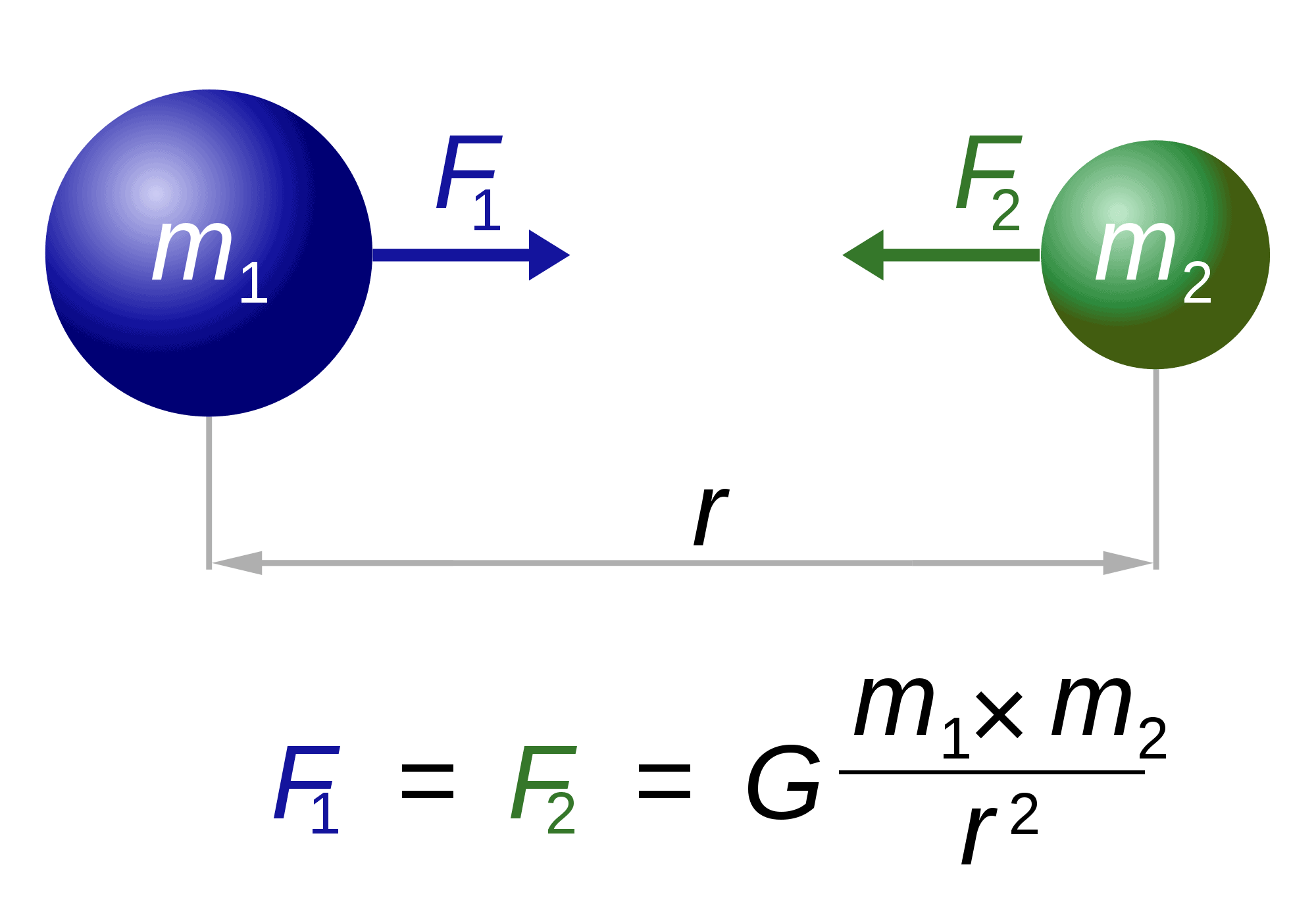
puhuessaan Newtonista hän on myös ”vastuussa” yhdestä maailman kuuluisimmista ja näyttävimmistä yhtälöistä: painovoimalaista.

laki kuvaa periaatteessa sitä, miten mitkä tahansa kaksi massojen m1 ja m2 muodostamaa kappaletta vetävät toisiaan puoleensa. Voima (F1, F2) on kääntäen verrannollinen niiden välisen etäisyyden neliöön (r). Ainoa jäljellä oleva tekijä, G, on gravitaatiovakio. Tämän vakion luonne on edelleen hämärän peitossa.

yleinen suhteellisuusteoria

lähes 200 vuoden ajan Newtonin laki määritteli mekaniikan ymmärrystasomme. Einsteinin työ 1900 — luvulla vei asiat seuraavalle tasolle-nämä kaksi saavutusta torni korkeimmat jalustat maailmassa fysiikan.

yleinen suhteellisuusteoria on pohjimmiltaan geometrinen gravitaatioteoria, joka yleistää Newtonin teorian ja tarjoaa yhtenäisen kuvauksen painovoimasta avaruuden ja ajan — tai aika-avaruuden-geometrisena ominaisuutena. Erityisesti Einstein osoitti paitsi, että on olemassa sellainen asia kuin ”aika-avaruus”, joka yhdistää kolme ulottuvuutta ajan neljänteen ulottuvuuteen, hän osoitti myös, että tämä aika-avaruus voi olla kaareva painovoiman avulla, ja kaarevuus on suoraan verrannollinen minkä tahansa aineen ja säteilyn energiaan ja liikemäärään.

termodynamiikan toinen laki

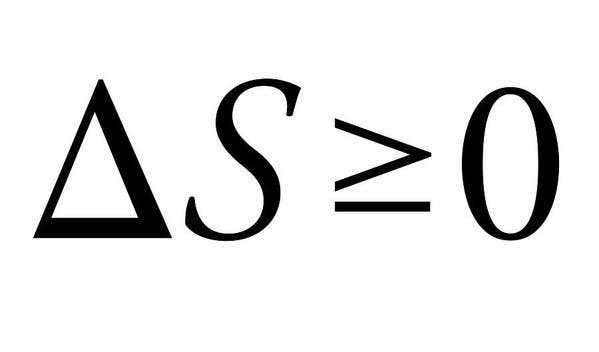
termodynamiikan toinen laki on, miksi maailmankaikkeudessa ei voi olla kivoja asioita. Termodynamiikan neljä lakia määrittelevät fysikaaliset suureet (lämpötila, Energia ja entropia), jotka luonnehtivat termodynaamisia systeemejä. Erityisesti toinen niistä erottuu tässä yksinkertaisuuden, mutta aivan massiivisten vaikutustensa vuoksi.

lain mukaan vuorovaikutuksellisten termodynaamisten systeemien entropioiden summan tulee aina kasvaa tai korkeintaan pysyä vakiona. Kun energia muuttuu muodosta toiseen tai aine liikkuu ympäriinsä, entropia (tai häiriö) suljetussa systeemissä kasvaa. Kaikki erot lämpötilassa, paineessa ja tiheydessä pyrkivät tasoittumaan jonkin ajan kuluttua

Maxwellin yhtälöt

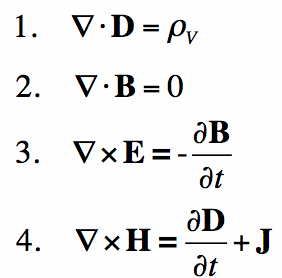
Yksinkertaisesti sanottuna Maxwellin yhtälöt ovat sähkömagnetismille sama kuin Newtonin laki on mekaniikalle. Ne luovat matemaattisen perustan klassiselle sähkömagnetismille, klassiselle optiikalle ja sähköpiireille. Niitä käytetään laajalti juuri siinä laitteessa, jossa luet tätä-periaatteessa kaikissa elektronisissa laitteissa.

Maxwellin lait kuvaavat, miten sähkö-ja magneettikentät syntyvät varauksista, virtauksista ja kenttien muutoksista. Merkittävä läpimurto oli osoitus siitä, että sähkö-ja magneettikentät etenevät valon nopeudella.

Eulerin identiteetti

lopuksi tämä on varsin mahdollisesti tyylikkäin yhtälö, äärimmäisen kaunis asia, koska siihen kuuluvat kaikki ”perusluvut”:

• 0, joka on neutraali yhteen-ja vähennyslaskussa;
• 1, joka on neutraali kerto-ja jakolaskussa;
• e joka on Eulerin luku (KS. yllä), luonnollisten logaritmien kanta;
• i on imaginaariyksikkö (KS.; ja
• π on pii, ympyrän kehän suhde sen halkaisijaan.

kaikkia näitä lukuja yhdistävän relaation löytäminen on suorastaan hengästyttävää, ja vaikuttaa varsin epätodennäköiseltä. Mielenosoitus ei ole aivan yksinkertainen, mutta näet sen täältä.

on vain osuvaa, että Stanfordin yliopiston matematiikan professori Keith Devlin kuvasi yhtälön sanoen, että ”kuin Shakespearen sonetti, joka vangitsee rakkauden olemuksen, tai maalaus, joka tuo esiin ihmismuodon kauneuden, joka on paljon enemmän kuin vain ihonmyötäinen, Eulerin yhtälö ulottuu olemassaolon syvyyksiin”

harvoin matematiikka ja fysiikka yhdistyvät yksinkertaisiin ja elegantteihin yhtälöihin — mutta kun niin käy, se on melkoinen näky.