Fibonaccin sekvenssi
Fibonaccin sekvenssi on lukusarja:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
seuraava luku löytyy laskemalla yhteen kaksi lukua ennen sitä:
- 2 Löytyy lisäämällä kaksi lukua ennen sitä (1+1),
- 3 löytyy lisäämällä kaksi numeroa ennen sitä (1+2),
- 5 on (2+3),
- ja niin edelleen!
esimerkki: seuraava numero yllä olevassa järjestyksessä on 21+34 = 55
se on niin yksinkertainen!
tässä on pidempi lista:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
saatko selville seuraavat numerot?
tekee spiraalin
kun teemme neliöitä noilla leveyksillä, saamme mukavan spiraalin:
Näetkö miten neliöt sopivat siististi yhteen?
esimerkiksi 5 ja 8 tekevät 13, 8 ja 13 tekevät 21 ja niin edelleen.
tämä spiraali löytyy luonnosta!
Katso: Nature,the Golden Ratio, ja Fibonacci
sääntö
Fibonaccin sekvenssi voidaan kirjoittaa ”sääntönä” (KS.sekvenssit ja sarjat).
ensin termit numeroidaan 0: sta eteenpäin näin:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
joten termiä numero 6 kutsutaan x6: ksi (joka on yhtä kuin 8).
|
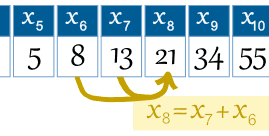
Example: the 8th term is x8 = x7 + x6 |
|
näin voidaan kirjoittaa sääntö:
sääntö on XN = XN−1 + XN−2
missä:
- xn on termiluku ”n”
- xn−1 on edellinen termi (n−1)
- xn−2 on sitä edeltävä termi (n−2)
esimerkki: termi 9 lasketaan näin:
=34
kultainen suhde

ja tässä on yllätys. Kun otetaan mikä tahansa kaksi peräkkäistä (yksi toisensa jälkeen) Fibonaccin lukua, niiden suhde on hyvin lähellä kultaista suhdelukua ”φ”, joka on noin 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
meidän ei tarvitse aloittaa 2: sta ja 3: sta, tässä valitsin satunnaisesti 192 ja 16 (ja sain järjestysnumeron 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
hyvien arvojen saaminen kestää kauemmin, mutta se osoittaa, että tähän ei pysty pelkästään Fibonaccin sekvenssi!
käyttämällä kultaista suhdelukua Fibonaccin lukujen laskemiseen
ja vielä yllättävämpää on, että voimme laskea minkä tahansa Fibonaccin luvun kultaisella suhteella:
xn = φn − (1−φ)n√5
vastaus tulee ulos kokonaislukuna, joka on täsmälleen sama kuin kahden edellisen termin yhteenlasku.
esimerkki: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
kun käytin laskinta tähän (vain syöttämällä kultaisen suhteen 6 desimaalin tarkkuudella) sain vastauksen 8.00000033 , tarkempi laskelma olisi lähempänä 8.
kokeile n=12 Ja katso, mitä saat.
Voit myös laskea Fibonaccin luvun kertomalla edellisen Fibonaccin luvun kultaisella suhteella ja sen jälkeen pyöristämällä (toimii luvuille yli 1):
esimerkki: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (pyöristetty)
joitakin mielenkiintoisia asioita
tässä on Fibonaccin sekvenssi taas:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
on mielenkiintoinen kuvio:
- Katso lukua x3 = 2. Joka 3. Numero on kerrannainen 2 (2, 8, 34, 144, 610, …)
- Katso lukua x4 = 3. Joka neljäs numero on kerrannainen 3 (3, 21, 144,…)
- Katso lukua x5 = 5. Jokainen 5. Numero on kerrannainen 5 (5, 55, 610,…)
ja niin edelleen (jokainen N: S numero on XN: n kerrannainen).
1/89 = 0, 011235955056179775…
huomaa muutaman ensimmäisen numeron (0,1,1,2,3,5) olevan Fibonaccin sekvenssi?
tavallaan ne kaikki ovat, paitsi moninumeroiset luvut (13, 21 jne.) päällekkäisiä, näin:
… jne …
0, 011235955056179775… = 1/89
termit nollan alapuolella
järjestysnumero toimii nollan alapuolella myös näin:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Todista itsellesi, että jokainen luku löytyy laskemalla yhteen sitä edeltävät kaksi lukua!)
itse asiassa nollan alapuolella olevalla jaksolla on samat numerot kuin nollan yläpuolella olevalla jaksolla, paitsi että ne seuraavat a +-+- … Kuvio. Se voidaan kirjoittaa näin:
x−n = (-1) n+1 xn
, jonka mukaan termi ”−n” on yhtä kuin (-1)n+1 kertaa termi ”n”, ja arvo (-1)n+1 tekee siististi oikean +1, -1, +1, -1, … Kuvio.
historia
Fibonacci ei ollut ensimmäinen, joka tiesi sekvenssistä, se tunnettiin Intiassa satoja vuosia aiemmin!

Fibonaccista mies
hänen oikea nimensä oli Leonardo Pisano Bogollo, ja hän asui vuosina 1170-1250 Italiassa.
”Fibonacci” oli hänen lempinimensä, joka tarkoittaa karkeasti ”Bonaccin poikaa”.
sen lisäksi, että hän oli kuuluisa Fibonaccin sekvenssistä, hän auttoi hindulais-arabialaisten numeroiden levittämisessä (kuten nykyiset numeromme 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) Euroopan kautta roomalaisten numeroiden sijasta (I, II, III, IV, V jne.). Se on säästänyt meiltä kaikilta paljon vaivaa! Kiitos, Leonardo.

Fibonaccin päivä
Fibonaccin päivä on marraskuun 23.päivä, koska siinä on järjestykseen kuuluvat numerot ”1, 1, 2, 3”. Joten seuraava marraskuu 23 kerro kaikille!

Leave a Reply