”Interstellar” – elokuvan lipputulomenestyksen myötä monet ovat innostuneet madonreikien mahdollisuuksista tähtienvälisen liikenteen välineenä. Vaikka tällä hetkellä ei ole todisteita siitä, että tällaisia eksoottisia esineitä olisi luonnossa, on mahdollista, että ne olisi voitu luoda keinotekoisesti, ehkä korkeamman ulottuvuuden säieteorian versioista ja aika-avaruuden perustavuusvaahdon suunnittelusta. Madonreikätutkimus on tänä päivänä jännittävä aihe, josta julkaistaan vuosittain kymmeniä tutkielmia vertaisarvioiduissa lehdissä, mutta sen alkuperästä kannattaa muistuttaa — ja se alkaa yllättävästä paikasta.

vuonna 1915 Albert Einstein julkaisi yleisen suhteellisuusteoriansa, painovoiman kuvauksensa, joka määrittelee siististi, miten kappaleet vetävät toisiaan puoleensa ja vaikuttavat ympäröivään tilaan ja aikaan. Monia vuosia myöhemmin amerikkalainen fyysikko John Wheeler kolikoi lauseen ”avaruus kertoo materialle, miten liikutaan, ja materia kertoo avaruudelle, miten käyrä tehdään”. Einstein kuvasi painovoiman aika-avaruuden kaarevuuden ilmentymänä. Yleinen suhteellisuusteoria on jatkuva kenttäteoria vastakohtana aineen hiukkasteorialle, joka johti kvanttimekaniikkaan.

Einstein oli myös mukana kehittämässä kvanttimekaniikkaa, teoriaa, joka kuvaa subatomisia hiukkasia. Hän ei kuitenkaan ollut täysin tyytyväinen sen luontaisiin epävarmuustekijöihin ja todennäköisyyteen. Niinpä hän työskenteli vuonna 1935 Nathan Rosenin kanssa elektronien kenttäteorian tuottamiseksi yleistä suhteellisuusteoriaa käyttäen. Heidän tutkielmansa oli otsikoitu ”the Particle Problem in the General theory of Relativity”. Einstein ja Rosen tutkivat atomistisen aineen ja sähkön teorian mahdollisuutta, joka, lukuun ottamatta epäjatkuvuuksia (singularities) alalla, käytti mitään muita muuttujia kuin yleisen suhteellisuusteorian kuvaus (metriikka) ja Maxwellin sähkömagneettinen teoria. Yksi seuraus oli, että alkeellisimman varautuneen hiukkasen havaittiin olevan yksi nollamassainen.

lopulta heidän tuottamansa oli jotain varsin omaperäistä. Ne alkoivat yhtälöillä pallosymmetriselle massajakaumalle, jota jo käytettiin mustille aukoille ja joka tunnetaan Schwarzschildin ratkaisuna,

$$DS^2 = -\dfrac{1}{1-2m/r}dr^2 – r^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)DT^2$

missä \(ds^2\) on metriikka ja \(M=GM/C^2\) pallokoordinaateilla \((r,\Theta,\Phi)\) ja aika \(t\).

he suorittivat koordinaattimuunnoksen poistaakseen alueen, joka sisältää kaarevuussingulariteetin, mustien aukkojen ja vastaavien ilmiöiden aiheuttaman avaruuden kaarevuuden epäjatkuvuuden. Singulariteetti \(R=2M\) poistettiin koordinaattimuunnoksella \(u^2 = r – 2M\), jolloin saatiin lopullinen ratkaisu,

$$DS^2 = -4(U^2 + 2M)du^2 – (u^2 + 2m)^2 d\Omega^2 + \dfrac{U^2}{u^2 + 2M} DT^2$$

missä \(d\Omega^2 = d\theta^2 + \Sin^2\theta d\PHI^2\).

tämä ratkaisu oli matemaattinen esitys fyysisestä avaruudesta kahden asymptoottisesti litteän arkin muodostamalla avaruudella, jota yhdisti silta tai Schwarzschildin madonreikä, jonka ”kurkku”. Tämä yhdistää kaksi arkkia ja analogisesti kaksi erillistä osaa todellisesta, kolmiulotteisesta maailmankaikkeudesta. Kuvassa 1 näkyy madonreikää ympäröivä tila, jossa ylä-ja alapuolella oleva tila muuttuu tasaiseksi ”reunoista”, kun loitonnat äärettömyyteen.

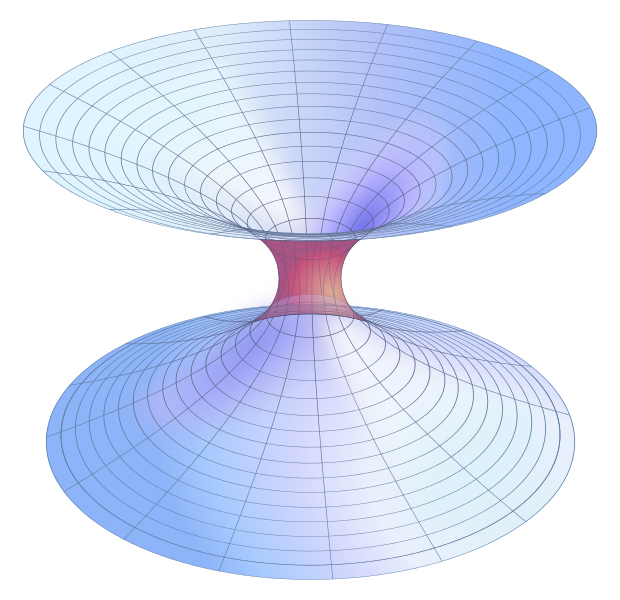
nyt tämä ei ollut Läpitunkeva madonreikä, sillä jouduimme odottamaan fyysikoiden John Wheelerin saapumista 1950-luvulla ja Kip Thornen saapumista 1980-luvulla. Vuonna 1987 Thorne ja hänen kollegansa Michael Morris pystyivät Carl Saganin rohkaisemana luomaan matemaattisen kuvauksen, metriikan, kuvaamaan pallosymmetristä ja staattista madonreikää, jolla on todellinen, äärellinen ympärysmitta. Tässä oli koordinaatisto, joka pieneni negatiivisesta äärettömyydestä minimaalisesti kaarevassa avaruudessa — minimiarvoon, jossa kurkku sijaitsi, ja sitten kasvoi kurkusta positiiviseen äärettömyyteen-erilaisessa minimaalisesti kaarevassa tilassa. Tämän ratkaisun erityispiirre on, että sillä ei ole tapahtumahorisonttia — toisin kuin mustalla aukolla. Thornen ja Morrisin paperi oli otsikoitu ”Wormholes in Space-time and their use for Interstellar Travel: a Tool for Teaching General Relativity”. Tämä paperi auttoi luomaan madonreikätutkimuksen uudeksi akateemisen tutkimuksen alueeksi.

sen jälkeen on julkaistu monia tutkielmia ja tehty tähtitieteellisiä tutkimuksia, joissa on tutkittu kauimpia tähtiä ja galakseja etsien luonnollisia madonreikiä. Yhtäkään ei ole vielä tunnistettu, mutta muistakaa tämän tutkimusalan alkuperä — Einsteinin-Rosenin silta ei ollut läpäistävä madonreikä, eikä se ollut kirjoittajan aikomus tuottaa sellainen, mutta he tuottivat ensimmäisen matemaattisen kuvauksen madonreiästä. Heidät pitäisi muistaa tästä. Tieteen tutkimus tuottaa usein jotain varsin odottamatonta, jonka vaikutukset ulottuvat kauas tutkijoiden alkuperäisiä tarkoitusperiä pidemmälle.

Kelvin F. Kauan

tämän artikkelin julkaisun jälkeen lehtemme Principium on julkaissut kaksi numeroa (numerot 9 & 10), joissa käsitellään tarkemmin madonreikiä ja Einsteinin-Rosenin siltaa. Nämä kysymykset ovat myös yksityiskohtaisesti yksi päivä symposium ”Interstellar Wormholes: Physics and Practical Realisation” järjesti Initiative for Interstellar Studies yhteistyössä British Interplanetary Societyn kanssa.