Articles

Easy Permutations and Combinations

by admin

I ’ ve always confused ”permutation” and ”combination” — which one ’ s which?

tässä on helppo tapa muistaa: permutaatio kuulostaa monimutkaiselta, eikö niin? Ja se on. Permutaatioissa jokaisella yksityiskohdalla on merkitystä. Alice, Bob ja Charlie on erilainen kuin Charlie, Bob ja Alice (lisää ystäviesi nimet tähän).

yhdistelmät sen sijaan ovat aika helppoja. Yksityiskohdilla ei ole väliä. Alice, Bob ja Charlie on sama kuin Charlie, Bob ja Alice.

Permutaatiot ovat luetteloille (järjestysasioita) ja yhdistelmät ryhmille (järjestyksellä ei ole väliä).

”yhdistelmälukkoa” pitäisi oikeastaan kutsua ”permutaatiolukoksi”. Numerojärjestyksellä on väliä.

Helpot Permutaatiot ja yhdistelmät

todellinen ”yhdistelmälukko” hyväksyisi sekä 10-17-23 että 23-17-10 oikeiksi.

permutaatiot: karvaiset yksityiskohdat

aloitetaan permutaatioista eli kaikista mahdollisista tavoista tehdä jotain. Käytämme hienostelevaa termiä ”permutaatio”, joten välitämme jokaisesta yksityiskohdasta, mukaan lukien jokaisen tavaran järjestyksestä. Sanotaan, että meillä on 8 ihmistä:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

kuinka monella tavalla voimme jakaa 1., 2. ja 3. sijan kahdeksan kilpailijan kesken? (Kulta / Hopea/Pronssi)

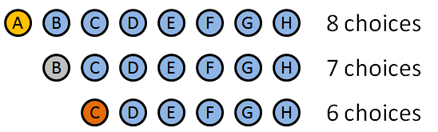
permutaatioesimerkki mitalit

aiomme käyttää permutaatioita, koska järjestys, jossa nämä mitalit jaetaan, ratkaisee. Näin se hajoaa:

  • kultamitali: 8 valintaa: A B C D E F G H (nokkelaa miten sain nimet vastaamaan kirjaimia, eh?). Sanotaan, että A voittaa kullan.
  • hopeamitali: 7 valintaa: B C D E F G H. oletetaan, että B voittaa hopean.
  • pronssimitali: 6 valintaa: C D E F G H. sanotaan vaikka… C voittaa pronssin.

valitsimme tiettyjä voittajia, mutta yksityiskohdilla ei ole väliä: meillä oli ensin 8 vaihtoehtoa, sitten 7, sitten 6. Vaihtoehtojen kokonaismäärä oli $8 * 7 * 6 = 336$.

Katsotaanpa yksityiskohtia. Piti tilata 3 henkeä kahdeksasta. Tätä varten aloitimme kaikilla vaihtoehdoilla (8) sitten otimme ne pois yksi kerrallaan (7, sitten 6), kunnes mitalit loppuivat.

tiedämme, että faktori on:

\displaystyle{ 8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 }

valitettavasti se tekee liikaa! Haluamme vain $8 * 7 * 6$. Miten voimme” pysäyttää ” faktorin 5?

tässä permutaatiot viilenevät: huomaa, miten haluamme päästä eroon $5 * 4 * 3 * 2 * 1$. Mikä toinen nimi tälle on? 5 factorial!

So, if we do 8!/5! saamme:

\displaystyle{\frac{8!}{5!} = \frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \cdot 6}

ja miksi käytimme numeroa 5? Koska se jäi yli, kun poimimme 3 mitalia 8: sta. Parempi tapa kirjoittaa tämä olisi siis:

\displaystyle{\frac{8!}{(8-3)!}}

missä 8!/(8-3)! on vain hieno tapa sanoa ” Käytä 3 ensimmäistä numeroa 8!”. Jos meillä on n kohteita yhteensä ja haluamme valita k: n tietyssä järjestyksessä, saamme:

\displaystyle{\frac{n!{(n-k)!}}

ja tämä on fancy permutaatiokaava: sinulla on n alkioita ja haluat löytää kuinka monta tapaa k alkioita voidaan järjestää:

\displaystyle{P(n,k) = \frac{n!{(n-k)!}}

yhdistelmät, Ho!

yhdistelmät ovat helppoja. Järjestyksellä ei ole väliä. Voit sekoittaa sen ja se näyttää samalta. Sanotaan, että olen kitupiikki eikä minulla ole varaa erillisiin kulta -, hopea-ja pronssimitaleihin. Itse asiassa minulla on varaa vain tyhjiin peltipurkkeihin.

kuinka monella tavalla voin antaa 3 peltipurkkia 8 hengelle?

no, tässä tapauksessa sillä, missä järjestyksessä ihmiset valitaan, ei ole väliä. Jos annan tölkin Alicelle, Bobille ja Charlielle, se on sama kuin antaisin Charlielle, Alicelle ja sitten Bobille. Joka tapauksessa he ovat yhtä pettyneitä.

tämä nostaa esiin mielenkiintoisen seikan — meillä on tässä vähän irtisanomisia. Alice Bob Charlie = Charlie Bob Alice. Hetken, katsotaanpa vain selvittää, kuinka monella tavalla voimme järjestää 3 henkilöä.

no, meillä on 3 vaihtoehtoa ensimmäiselle, 2 toiselle ja vain 1 viimeiselle. Joten meillä on $3 * 2 * 1$ tapoja järjestää uudelleen 3 henkilöä.

odota hetki… tää näyttää vähän permutaatiolta! Huijasit minua!

todellakin tein. Jos sinulla on n ihmisiä ja haluat tietää, kuinka monta järjestelyä on heille kaikille, se on vain n factorial tai N!

joten, jos meillä on 3 peltipurkkia annettavana, niitä on 3! tai 6 variaatiota jokaiselle valinnalle, jonka valitsemme. Jos haluamme selvittää, kuinka monta yhdistelmää meillä on, luomme vain kaikki permutaatiot ja jaamme kaikki irtisanomiset. Meidän tapauksessamme, saamme 336 permutaatiot (ylhäältä), ja me jakaa 6 irtisanomiset kunkin permutation ja saada 336/6 = 56.

yleinen kaava on

\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}

, joka tarkoittaa ”Etsi kaikki tavat valita k-ihmiset N: stä ja jaa K: lla! variantti”. Tätä kirjoitettaessa saadaan kombinaatiokaava eli K-alkioiden yhdistämistapojen määrä joukosta n:

\displaystyle{C(n,k) = \frac{n!{(n-k)!k!}}

joskus C(n,k) kirjoitetaan seuraavasti:

\displaystyle{\binom {n}{k}}

, joka on binomikerroin.

muutama esimerkki

tässä muutama esimerkki yhdistelmistä (järjestyksellä ei ole väliä) permutaatioista (järjestyksellä on väliä).

  • yhdistelmä: poimitaan 3 hengen joukkue 10 hengen ryhmästä. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    permutaatio: presidentin, varapresidentin ja Vesipojan valitseminen 10 hengen ryhmästä. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • yhdistelmä: valitaan 3 jälkiruokaa 10 hengen menusta. C (10,3) = 120.

    permutaatio: listaamalla 3 suosikkijälkiruokaasi järjestykseen 10: n menusta. P (10,3) = 720.

älä opettele kaavoja ulkoa, ymmärrä miksi ne toimivat. Yhdistelmät kuulostavat yksinkertaisemmilta kuin permutaatiot, ja niitä ne ovatkin. Sinulla on vähemmän yhdistelmiä kuin permutaatioita.

muut tämän sarjan Virat

  1. Helpot Permutaatiot ja yhdistelmät
  2. Navigoi ruudukossa yhdistelmien ja permutaatioiden avulla
  3. miten ymmärtää yhdistelmät kertolaskun avulla
  4. miksi kerrotaan yhdistelmät?