Definite Integrals
saatat haluta lukea johdannon integraatioon ensin!
integraatio
|
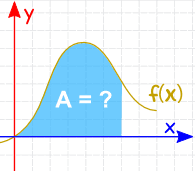
integraation avulla voidaan löytää alueita, tilavuuksia, keskipisteitä ja monia hyödyllisiä asioita. Usein sitä kuitenkin käytetään etsimään funktion kuvaajan alle jäävä alue näin: |
 |
|
|
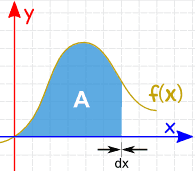
alue voidaan löytää lisäämällä viivoja, jotka lähestyvät leveydeltään Nollaa: ja on Integraatiosääntöjä, joiden avulla saadaan vastaus. |
 |
notaatio
”integraalin” symboli on tyylikäs ”s” (”summalle”, viipaleiden yhteenlaskun idea):
integraalisymbolin jälkeen laitamme funktion, jonka haluamme löytää integraalin (jota kutsutaan Integrandiksi).
ja lopuksi DX, jolloin viipaleet menevät X-suuntaan (ja lähestyvät nollaa leveydeltään).
määräinen integraali
Määräisellä integraalilla on alku-ja loppuarvot: toisin sanoen on intervalli .
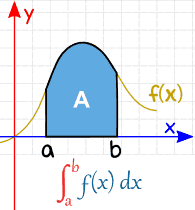
a ja b (niin kutsutut rajat, rajat tai rajat) laitetaan ”S”: n alaosaan ja yläosaan näin:
 |
 |
|
| Definite Integral (from a to b) |
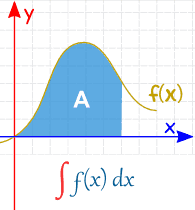
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
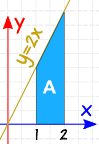
esimerkki: mikä on 2 ∫ 1 2x DX
meiltä pyydetään määräistä integraalia, joka on 1-2, 2x DX
ensin on löydettävä määrittelemätön kiinteä.
integroinnin sääntöjä käyttäen huomaamme, että ∫2x DX = x2 + c
laske nyt, että 1: ssä ja 2:
- At x=1: ∫2x DX = 12 + c
- At x=2: ∫2x DX = 22 + C
vähennä:
ja ”C” jää pois … Definiittisillä Integraaleilla voidaan siis sivuuttaa C.
tulos:

tarkista: näin yksinkertaisella muodolla yritetään laskea pinta-ala myös geometrialla:
a = 2+42 × 1 = 3
kyllä, sen pinta-ala on 3.
(Jee!)
notaatio: Voimme näyttää epämääräisen integraalin (ilman +C: tä) hakasulkeiden sisällä, rajojen a ja b jälkeen näin:
esimerkki (jatkoa)
hyvä tapa näyttää vastauksesi:
=
kokeillaan toista esimerkkiä:
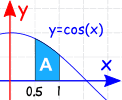
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
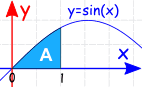
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
epämääräinen integraali on:∫sin(x) dx = −cos(x) + c
koska olemme menossa 0, voimmeko vain laskea integraalin x=1?
– cos (1) = -0, 540…
Mitä? Onko se negatiivinen? Mutta se näyttää graafissa positiiviselta.
hyvin… teimme virheen!
koska meidän on vähennettävä integraali pisteessä x=0. Meidän ei pitäisi olettaa, että se on nolla.
joten tehkäämme se kunnolla, vähentämällä toinen toisista:
=
That ’ s better!
mutta meillä voi olla negatiivisia alueita, kun käyrä on akselin alapuolella:
esimerkki:
cos(x) dx: n määräinen integraali 1: stä 3: een:
huomaa, että osa on positiivisia ja osa negatiivisia.
määräinen integraali selvittää nettoarvon.
Tehkäämme laskelmat:
=
hyppy on enemmän negatiivinen kuin positiivinen nettotuloksella -0,700….
joten meillä on tämä tärkeä asia muistaa:
yritä yhdistää cos(x) eri alku-ja loppuarvoilla nähdäksesi itse, miten positiiviset ja negatiiviset toimivat.
positiivinen pinta-ala
, mutta joskus haluamme, että kaikkia alueita käsitellään positiivisina (ilman, että akselin alapuolella olevaa osaa vähennetään).
tällöin on laskettava alueet erikseen, kuten tässä esimerkissä:

esimerkki: Mikä on kokonaispinta-ala välillä y = cos(x) ja x-akselin, X = 1-x = 3?
Tämä on samanlainen esimerkki kuin äsken, mutta nyt odotamme, että kaikki alue on positiivinen (kuvitelkaa, että meidän piti maalata se).
joten nyt on tehtävä osat erikseen:
- yksi X-akselin yläpuoliselle alueelle
- yksi X-akselin alapuoliselle alueelle
käyrä ylittää x-akselin kohdassa x = π/2, joten meillä on:
1: stä π/2:
= sin(π/2) − Sin(1)
From π/2 to 3:
cos(x) dx
= sin(3) − sin(π/2)
div> = 0, 141… – 1
viimeinen tulee negatiivisena, mutta haluamme sen olevan positiivinen, joten:
kokonaispinta-ala = 0,159… + 0.859… = 1.018…
Tämä on hyvin erilainen kuin edellisessä esimerkissä.
jatkuva
Kyllä, integroimamme funktion on oltava jatkuva A: n ja b: n välillä: ei reikiä, hyppyjä tai pystysuoria asymptootteja (jossa funktio suuntaa ylös / alas kohti äärettömyyttä).
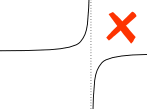
esimerkki:
a: n ja b: n välinen pystysuora asymptootti vaikuttaa määrättyyn integraaliin.
ominaisuudet
pinta − ala alle
integraali lisää akselin yläpuolisen alueen, mutta vähentää alla olevan alueen,”nettoarvoksi”:
funktioiden lisääminen
f+g: n integraali on yhtä suuri kuin F plus: n integraali g: n integraali:
a
/div>
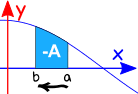
intervallin suunnan kääntäminen antaa alkuperäisen suunnan negatiivisen.
![]()


Leave a Reply