arvioi Cohenin Kappa

Kappan arvo voi olla alle 0 (negatiivinen). Pistemäärä 0 tarkoittaa, että ratersien välillä on satunnainen sopimus, kun taas pistemäärä 1 tarkoittaa, että ratersien välillä on täydellinen sopimus. Siksi pistemäärä, joka on alle 0 tarkoittaa, että on vähemmän yhteisymmärrystä kuin satunnainen sattuma. Alla, aion näyttää kaavan selvittää tämän, mutta on tärkeää, että tutustut kuva 4 on vahva ymmärrys.

syy, miksi korostin kahta ruutua, selviää hetken kuluttua, mutta nyt, sallikaa minun hajottaa jokainen ruutu.

a => molempien ratamiesten kertomat esiintymät pitivät paikkansa. Rataajat ovat samaa mieltä.

b => yhteensä rater 2: n sanoma oli virheellinen, mutta Rater 1: n sanoma oli oikea. Tämä on erimielisyyttä.

C => yhteensä rater 1: n sanoma oli virheellinen, mutta Rater 2: n sanoma oli oikea. Tämäkin on erimielisyyttä.

d => molempien Ratamiesten kertomat tapaukset olivat virheellisiä. Rataajat ovat samaa mieltä.

selvittääksemme kappa-arvon meidän on ensin tiedettävä sopimuksen todennäköisyys (tämä selittää, miksi korostin sopimuksen diagonaalia). Tämä kaava saadaan laskemalla yhteen niiden testien lukumäärä, joissa rataajat ovat samaa mieltä, ja jakamalla se sitten testien kokonaismäärällä. Kuvan 4 esimerkin avulla tämä tarkoittaisi (A + D)/(A + B+ C+ D).

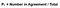
täydellistä! Seuraava askel on selvittää satunnaisen sopimuksen todennäköisyys. Käyttämällä kuva 4 oppaana, odotusarvo on kokonaismäärä kertaa, että Rater 1 sanoi oikein jaettuna kokonaismäärä tapauksia, kerrottuna kokonaismäärä kertaa, että Rater 2 sanoi oikein jaettuna kokonaismäärä tapauksia, lisätään kokonaismäärä kertaa, että Rater 1 sanoi virheellinen kerrottuna kokonaismäärä kertaa, että Rater 2 sanoi virheellinen. Se on paljon tietoa ottaa siellä niin kuvassa 6 olen muotoillut tämän yhtälön käyttäen grid edellä.

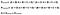
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

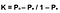
Suuri! Pystyt nyt erottamaan luotettavuuden ja pätevyyden, selittää Cohenin kappa ja arvioi sitä. Tämä tilasto on erittäin hyödyllinen, vaikka koska olen ymmärtänyt, miten se toimii, uskon nyt, että se voi olla alikäytetty optimoitaessa algoritmeja tiettyyn metriin. Lisäksi Cohenin kappa tekee hyvää työtä myös sekä moniluokkaisten että epätasapainoisten luokkaongelmien mittaamisessa.

P. S. Jos on jotain, että haluat minun kattaa tekemistä Data Science, voit ohjata viestin minulle Twitterissä @KurtisPykes tai jätä vastaus tähän viestiin.