Merian-Erbenin kartta (1652) Wikipediassa

tämän kuun matematiikkapalapeli on peräisin vuodelta 1735, jolloin sen ensimmäisenä ratkaisi sveitsiläinen matemaatikko ja fyysikko Leonhard Euler.

palapeliä kutsutaan Königsbergin seitsemäksi sillaksi. Se perustuu oikeaan kaupunkiin, silloiseen Preussiin, nykyiseen Kaliningradiin Venäjällä. Kaupunkia halkoo joki, jonka välissä on kaksi saarta ja alajuoksulla joki halkoo kaupungin uudelleen.

ongelma on petollisen yksinkertainen: saarella on (tai oli Eulerin aikana) seitsemän siltaa, jotka yhdistävät kaksi saarta ja kaupungin alajuoksun osat toisiinsa. Euler mietti, voisiko ihminen kävellä jokaisen seitsemän sillan yli kerran ja vain kerran koskettaakseen kaupungin jokaista osaa. Aloittaminen ja lopettaminen samaan kohtaan ei ollut vaatimus.

tässä on kartta, jonka avulla voit yrittää ratkaista ongelman itse:

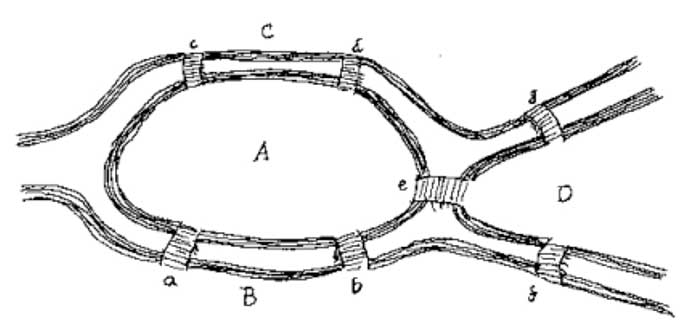
mikä mielestäsi on enemmän tärkeää ratkaista tämä ongelma: siltojen lukumäärä tai kunkin sillan sijainti?

vastaus: siltojen määrä.

Euler todisti, että siltojen määrän täytyy olla parillinen luku, esimerkiksi kuusi siltaa seitsemän sijaan, jos haluaa kävellä jokaisen sillan yli kerran ja matkustaa Königsbergin jokaiseen osaan. Ratkaisu pitää jokaista siltaa päätepisteenä, huippupistettä matemaattisesti ja kunkin sillan välisiä yhteyksiä (huippupiste). Euler tajusi, että vain parillinen määrä siltoja antoi oikean tuloksen siitä, että pystyi koskettamaan kaupungin jokaista osaa ylittämättä siltaa kahdesti.

Euler käytti matematiikkaa todistaakseen, että oli mahdotonta ylittää kaikki seitsemän siltaa vain kerran ja käydä Königsbergin jokaisessa osassa. Näin hän käynnisti joukon löytöjä ja oivalluksia siitä, miten avaruus ja risteävät tilat voidaan määritellä, sekä niiden ominaisuudet. Yksityiskohtainen kuvaus Eulerin ratkaisu Wikipedia linkki tämän artikkelin alla.

Jos olet joskus nähnyt esimerkiksi Mobiuksen liuskan, olet nähnyt esimerkin topologiasta, matemaattisesta tutkimusalasta, joka on kehittynyt Eulerin ratkaisusta tähän ongelmaan. Topologia käsittelee avaruutta ja sitä, miten asiat yhdistävät toisiaan, sekä avaruuden jatkuvuutta ja rajoja. Topologia tutkii myös sitä, miten avaruuden ominaisuudet muuttuvat eivätkä muutu avaruuden laajentuessa tai supistuessa.

laskennassa topologiasta on hyötyä sen ymmärtämisessä, mitä verkostoja (polkuja) data voi kulkea missä tahansa järjestelmässä, sekä miten tietojoukot voivat liittyä toisiinsa. Seitsemän sillat Königsbergin on myös samanlainen kuin toinen yhteinen computing ongelma kutsutaan joskus matkustava Myyntimies ongelma, jossa yrität löytää tehokkain reitti annetaan joukko rajoituksia, kuten seitsemän siltaa Eulerin ongelma.

Ei-matemaatikot (todennäköisesti sinä, ehdottomasti minä) kokevat kiertävän myyntimiehen ongelman aina, kun nousemme junaan tai bussiin. The Traveling Salesman Problem is mietitään tehokkain tapa matkustaa välillä paria kaupunkien tietyn välimatkan. Rajallisilla reiteillä kulkevien niukkojen resurssien (junat, bussit) hallinta on täydellinen ongelma tietokoneen ratkaistavaksi, koska tietokoneet ovat nopeampia ja tehokkaampia. Mutta ensin tarvitsemme Euler ja muut toteamaan ongelman ja määritellä ratkaisuja matematiikka. Sitten ohjelmoimme tietokoneemme laskemaan.

topologia käsittelee myös joukko-oppia, miten asioiden ryhmät voidaan lajitella joukoiksi, jotta voidaan tunnistaa yhteisiä elementtejä muiden ryhmien kanssa sekä ainutlaatuisia alkuaineita. Venn-Diagrammi on hyvä esimerkki joukosta. Ja ohjelmointi joutuu joskus lajittelemaan dataa eri tavoin. Mikä lajittelumenetelmä toimii tilanteeseen parhaiten, voidaan määrittää joukko-opin avulla.

ja mitä tapahtui Eulerin ajan seitsemälle sillalle? Kaksi ei selvinnyt toisesta maailmansodasta, vaan kaksi siltaa purettiin ja korvattiin yhdellä moottoritiellä. Kolmesta jäljellä olevasta sillasta yksi rakennettiin uudelleen vuonna 1935 ja kaksi muuta ovat Eulerin tuntemia. Ja tietenkin, Königsberg, Preussi on muuttanut nimensä Kaliningrad, Venäjä.

Lue lisää

Königsbergin seitsemän siltaa

topologia auttaa ihmisaivojen kartoittamisessa

Mobiuksen kaistale