Johdanto

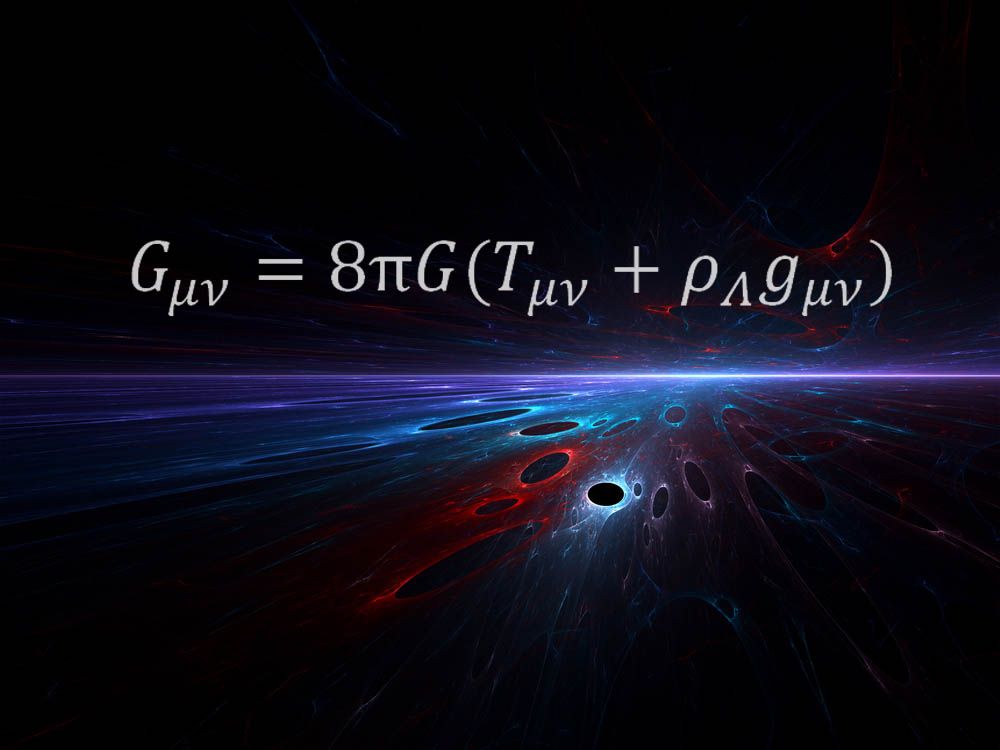
matemaattinen yhtälöt eivät ole vain hyödyllisiä — monet ovat melko kauniita. Ja monet tiedemiehet myöntävät, että he ovat usein mieltyneitä tiettyihin kaavoihin, eivät vain niiden tehtävän vuoksi, vaan niiden muodon ja niiden sisältämien yksinkertaisten, runollisten totuuksien vuoksi.

vaikka tietyt kuuluisat yhtälöt, kuten Albert Einsteinin E = mc^2, kahmivat suurimman osan julkisesta kunniasta, monilla vähemmän tutuilla kaavoilla on mestarinsa tutkijoiden keskuudessa. LiveScience kysyi fyysikoilta, tähtitieteilijöiltä ja matemaatikoilta heidän lempiyhtälöitään; tässä mitä löysimme:

yleinen suhteellisuusteoria

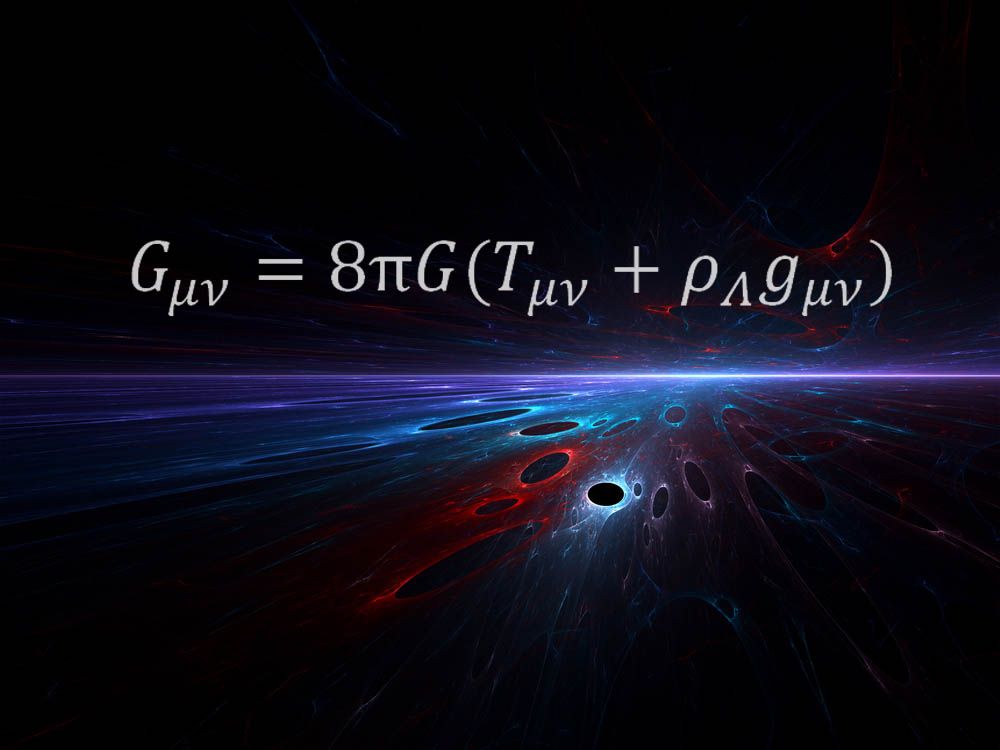
yllä olevan yhtälön muotoili Einstein osana uraauurtavaa yleistä suhteellisuusteoriaansa vuonna 1915. Teoria mullisti sen, miten tiedemiehet ymmärsivät painovoiman kuvaamalla voiman avaruuden ja ajan rakenteen vääristymäksi.

”minusta on edelleen hämmästyttävää, että yksi tällainen matemaattinen yhtälö voi kuvata, mistä aika-avaruudessa on kyse”, sanoi Space Telescope Science Instituten astrofyysikko Mario Livio, joka nimesi yhtälön suosikikseen. ”Kaikki Einsteinin todellinen nerous sisältyy tähän yhtälöön.”

”tämän yhtälön oikea puoli kuvaa universumimme energiasisältöä (mukaan lukien” pimeä energia”, joka vauhdittaa nykyistä kosmista kiihtyvyyttä)”, Livio selitti. ”Vasen puoli kuvaa aika-avaruuden geometriaa. Tasa-arvo kuvastaa sitä, että Einsteinin yleisessä suhteellisuusteoriassa massa ja energia määräävät geometrian ja samalla kaarevuuden, joka on niin sanotun gravitaation ilmentymä.”

”se on hyvin tyylikäs yhtälö”, sanoi New Yorkin yliopiston fyysikko Kyle Cranmer ja lisäsi, että yhtälö paljastaa aika-avaruuden sekä aineen ja energian välisen suhteen. ”Tämä yhtälö kertoo, miten ne liittyvät toisiinsa – miten auringon läsnäolo vääntää aika-avaruutta niin, että Maa liikkuu sen ympäri kiertoradalla jne. Se kertoo myös, miten maailmankaikkeus kehittyi alkuräjähdyksen jälkeen ja ennustaa, että siellä pitäisi olla mustia aukkoja.”

standardimalli

toinen fysiikan hallitsevista teorioista, standardimalli kuvaa niiden perushiukkasten kokoelmaa, joiden ajatellaan nykyisin muodostavan kaikkeuden.

teoria voidaan kapseloida pääyhtälöön nimeltä standardimalli Lagrangian (nimetty 1700-luvulla eläneen ranskalaisen matemaatikon ja tähtitieteilijän Joseph Louis Lagrangen mukaan), jonka teoreettinen fyysikko Lance Dixon Kalifornian SLAC National Accelerator Laboratorysta valitsi suosikkikaavalleen.

”se on onnistuneesti kuvannut kaikki alkeishiukkaset ja voimat, joita olemme laboratoriossa tähän mennessä havainneet — painovoimaa lukuun ottamatta”, Dixon kertoi Livesciencelle. ”Siihen sisältyy tietenkin äskettäin löydetty Higgsin(like) bosoni, Phi kaavassa. Se on täysin itseoppinut kvanttimekaniikan ja erityisen suhteellisuusteorian kanssa.”

standardimalliteoria ei ole kuitenkaan vielä yhtynyt yleiseen suhteellisuusteoriaan, minkä vuoksi se ei voi kuvata painovoimaa.

Calculus

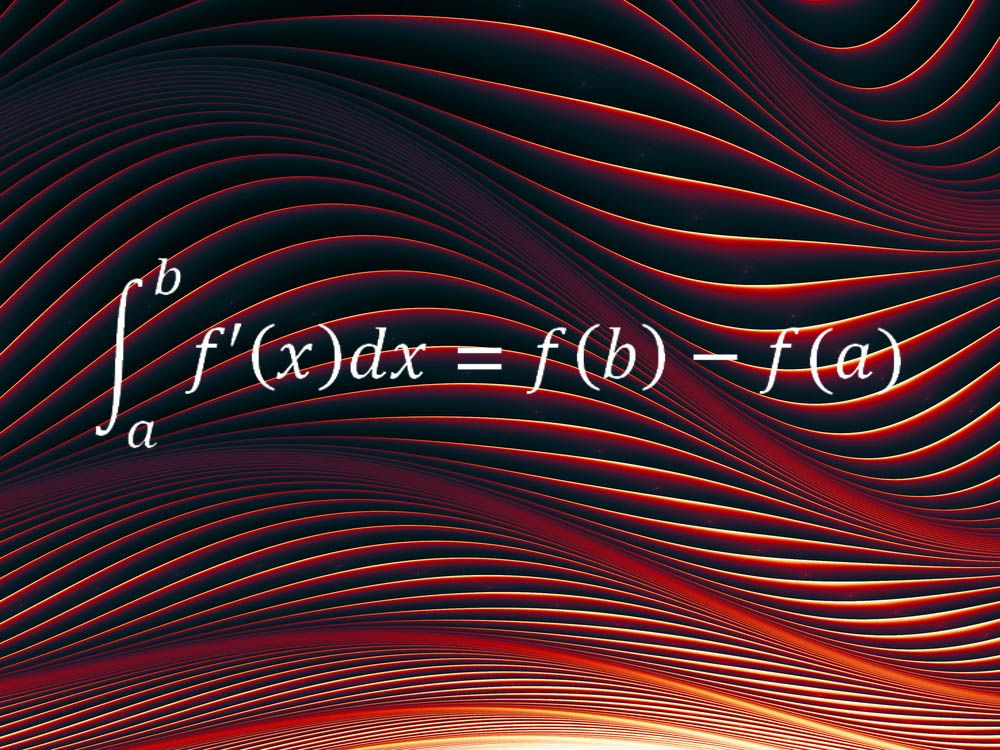
vaikka kaksi ensimmäistä yhtälöä kuvaavat universumimme tiettyjä puolia, voidaan toista suosikkiyhtälöä soveltaa kaikenlaisiin tilanteisiin. Calculuksen peruslause muodostaa Calculus-nimellä tunnetun matemaattisen menetelmän selkärangan ja yhdistää sen kaksi pääideaa, integraalin käsitteen ja derivaatan käsitteen.

”sanoo yksinkertaisissa sanoissa, että tasaisen ja jatkuvan suureen, kuten kuljetun matkan, nettomuutos tietyllä aikavälillä (ts. aikavälin päätepisteissä olevan määrän arvojen ero on yhtä suuri kuin kyseisen määrän muutosnopeuden integraali eli nopeuden integraali”, sanoi Fordhamin yliopiston matematiikan laitoksen puheenjohtaja Melkana Brakalova-Trevithick, joka valitsi tämän yhtälön suosikikseen. ”Calculuksen peruslauseen (FTC) avulla voidaan määrittää nettomuutos intervallilla perustuen muutosnopeuteen koko intervallilla.”

laskennan siemenet saivat alkunsa jo antiikin aikana, mutta suuren osan siitä kokosi 1600-luvulla Isaac Newton, joka käytti laskulaskentaa kuvaillessaan aurinkoa ympäröivien planeettojen liikkeitä.

Pythagoraan lause

”oldie but goodie” – yhtälö on kuuluisa Pythagoraan lause, jonka jokainen aloitteleva geometrian opiskelija oppii.

Tämä kaava kuvaa, miten minkä tahansa suorakulmaisen kolmion kohdalla hypotenuusan pituuden neliö c, (suorakulmaisen kolmion pisin sivu) on kahden muun sivun (a ja b) pituuksien neliöiden summa. Niinpä a^2 + b^2 = C^2

”ensimmäinen matemaattinen tosiasia, joka hämmästytti minua, oli Pythagoraan lause”, sanoi matemaatikko Daina Taimina Cornellin yliopistosta. ”Olin silloin lapsi, ja minusta tuntui niin ihmeelliseltä, että se toimii geometriassa ja se toimii numeroilla!”

1 = 0,999999999….

Tämä yksinkertainen yhtälö, jonka mukaan määrä 0,999, jota seuraa ääretön jono ysejä vastaa yhtä, on Cornellin yliopiston matemaatikko Steven strogatzin suosikki.

”rakastan sitä, miten yksinkertaista se on — kaikki ymmärtävät, mitä se sanoo — mutta kuinka provosoivaa se on”, Strogatz sanoi. ”Monet ihmiset eivät usko, että se voisi olla totta. Se on myös kauniisti tasapainossa. Vasen puoli edustaa matematiikan alkua; oikea puoli edustaa äärettömyyden mysteerejä.”

erityinen suhteellisuusteoria

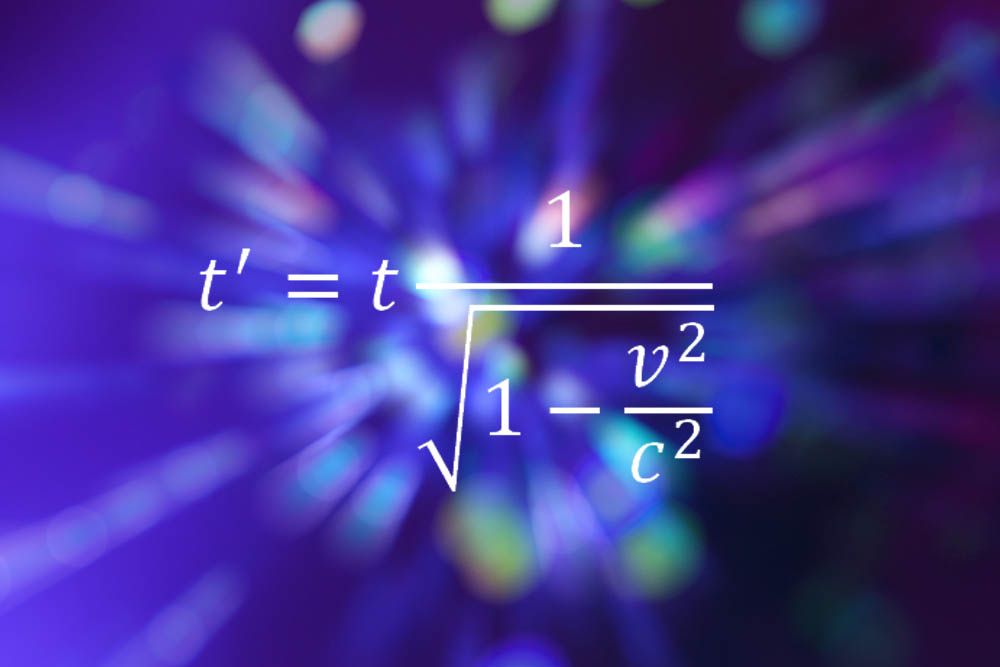
Einstein tekee listan uudelleen erikoisen suhteellisuusteorian kaavoillaan, jotka kuvaavat miten aika ja avaruus eivät ole absoluuttisia käsitteitä, vaan suhteellisia riippuen havaitsijan nopeudesta. Yllä oleva yhtälö näyttää, miten aika laajenee eli hidastuu, mitä nopeammin ihminen liikkuu mihin tahansa suuntaan.

”pointti on se, että se on todella hyvin yksinkertaista”, sanoi Bill Murray, hiukkasfyysikko Cernin laboratoriossa Genevessä. ”Ei ole mitään, mitä A-tason opiskelija ei voi tehdä, ei monimutkaisia johdannaisia ja jäljittää algebroja. Mutta se ilmentää aivan uutta tapaa katsoa maailmaa, koko asennetta todellisuuteen ja suhdettamme siihen. Yhtäkkiä jäykkä muuttumaton Kosmos pyyhkäistään pois ja korvataan henkilökohtaisella maailmalla, joka liittyy siihen, mitä havaitset. Siirryt universumin ulkopuolisesta, alas katsomisesta, johonkin sen sisällä olevaan komponenttiin. Mutta käsitteet ja matematiikan voi ymmärtää kuka tahansa, joka haluaa.”

Murray sanoi pitävänsä erityisiä suhteellisuusteorian yhtälöitä parempina kuin Einsteinin myöhemmän teorian monimutkaisempia kaavoja. ”En voisi koskaan noudattaa yleisen suhteellisuusteorian matematiikkaa”, hän sanoi.

Eulerin yhtälö

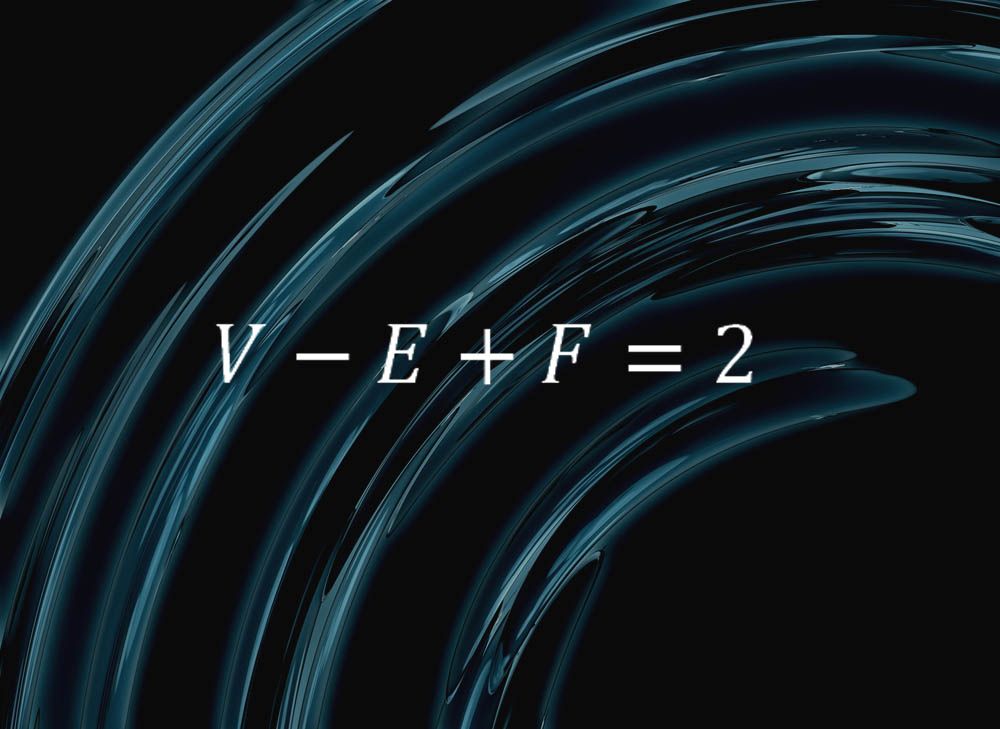
Tämä yksinkertainen kaava kiteyttää jotain puhdasta pallojen luonteesta:

”se sanoo, että jos leikkaat pallon pinnan ylöspäin tahkoiksi, särmiksi ja verticesiksi ja annat F: n olla tahkojen lukumäärä, E: n särmien lukumäärä ja V: n verticesin lukumäärä, saat aina V – E + F = 2”, sanoi Massachusettsin Williams Collegen matemaatikko Colin Adams.

”otetaan esimerkiksi tetraedri, joka koostuu neljästä kolmiosta, kuudesta särmästä ja neljästä kärkipisteestä”, Adams selitti. ”Jos puhalsit kovaa tetraedrin kanssa joustava kasvot, voit pyöristää sen pois osaksi pallo, joten siinä mielessä, pallo voidaan leikata neljään Kasvot, kuusi reunat ja neljä vertices. Ja näemme, että V-E + F = 2. Sama pätee pyramidiin, jossa on viisi tahkoa — neljä kolmiota ja yksi neliö — kahdeksan särmää ja viisi verticeä,” ja mikä tahansa muu tahkojen, särmien ja verticesin yhdistelmä.

” a very cool fakta! The combinatorics, vertices, reunat ja kasvot on syömällä jotain hyvin perustavanlaatuista noin Muoto Pallo,” Adams sanoi.

Eulerin-Lagrangen yhtälöt ja Noetherin lause

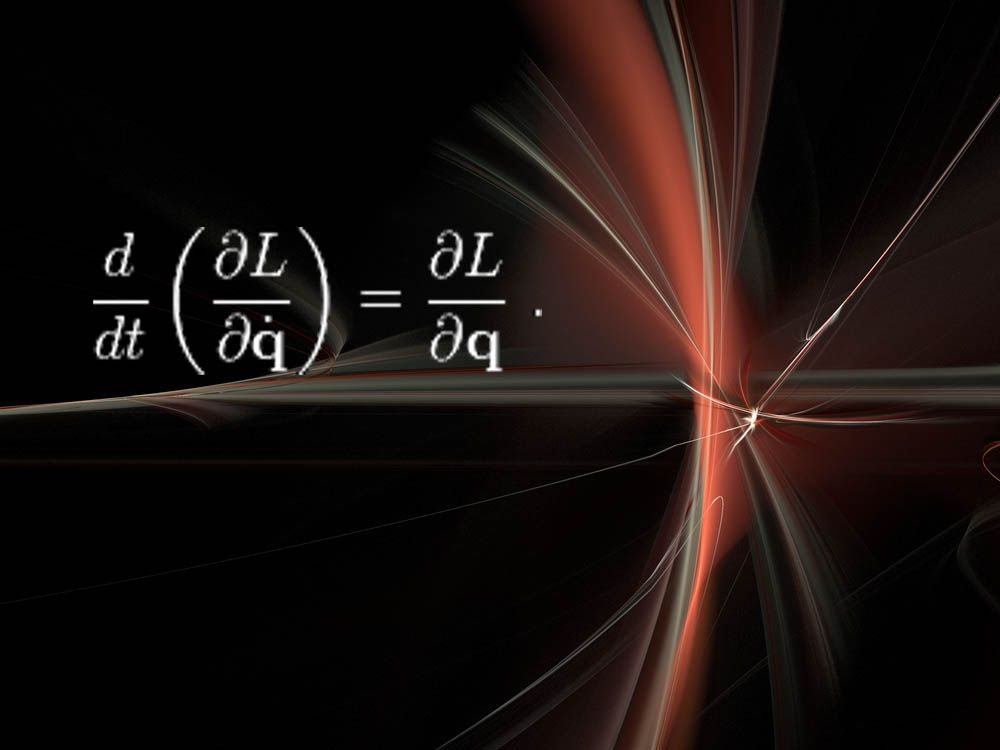
”nämä ovat aika abstrakteja, mutta hämmästyttävän voimakkaita”, NYU: n Cranmer sanoi. ”Siistiä on se, että tämä ajattelutapa fysiikasta on säilynyt joitakin fysiikan suuria vallankumouksia, kuten kvanttimekaniikka, suhteellisuusteoria jne.”

tässä L tarkoittaa lagrangia, joka on fysikaalisen systeemin, kuten jousien, tai vipujen tai perushiukkasten energian mitta. ”Tämän yhtälön ratkaiseminen kertoo, miten järjestelmä kehittyy ajan kanssa”, Cranmer sanoi.

Lagrangilaisen yhtälön spinoffia kutsutaan Noetherin lauseeksi 1900-luvun saksalaisen matemaatikon Emmy Noetherin mukaan. ”Tämä lause on todella perustavanlaatuinen fysiikalle ja symmetrialle”, Cranmer sanoi. ”Epävirallisesti lause on, että jos systeemillä on symmetria, on olemassa vastaava säilymislaki. Esimerkiksi ajatus siitä, että fysiikan peruslait ovat samat tänään kuin huomenna (ajan symmetria), merkitsee energian säilymistä. Ajatus siitä, että fysiikan lait ovat täällä samat kuin ulkoavaruudessa, viittaa liikemäärän säilymiseen. Symmetria on ehkä perusfysiikan ajo-käsite, joka johtuu ennen kaikkea myötävaikutuksesta.”

Callan-Symanzikin yhtälö

”Callan-symanzikin yhtälö on elintärkeä ensimmäisen periaatteiden yhtälö vuodelta 1970, olennaista kuvaamaan, kuinka naiivi odotukset epäonnistuvat kvanttimaailmassa”, sanoi teoreettinen fyysikko Matt strassler Rutgersin yliopistosta.

yhtälöllä on lukuisia sovelluksia, muun muassa sen avulla fyysikot voivat arvioida atomien ytimistä koostuvien protonin ja neutronin massan ja koon.

perusfysiikan mukaan kahden kappaleen välinen gravitaatiovoima ja sähköinen voima on verrannollinen niiden välisen etäisyyden käänteislukuun. Yksinkertaisella tasolla sama pätee voimakkaaseen ydinvoimaan, joka sitoo protonit ja neutronit yhteen muodostaen atomien ytimiä ja joka sitoo kvarkit yhteen muodostaen protoneja ja neutroneja. Pienet kvanttivaihtelut voivat kuitenkin hieman muuttaa voiman riippuvuutta etäisyydestä, millä on dramaattisia seurauksia voimakkaalle ydinvoimalle.

”se estää tätä voimaa vähenemästä pitkillä etäisyyksillä ja saa sen vangitsemaan kvarkkeja ja yhdistämään ne maailmamme protoneiksi ja neutroneiksi”, Strassler sanoi. ”Mitä Callan-Symanzik yhtälö tekee on suhteuttaa tämä dramaattinen ja vaikea-laskea vaikutus, tärkeä, kun on suurin piirtein koko protoni, hienovaraisempia mutta helpompi-laskea vaikutuksia, jotka voidaan mitata, kun on paljon pienempi kuin protoni.”

minimaalisen pinnan yhtälö

”minimaalisen pinnan yhtälö jotenkin koodaa kauniita saippuafilmejä, jotka muodosta johtorajoilla, kun kastat ne saippuavedessä”, sanoi matemaatikko Frank Morgan Williams Collegesta. ”Se, että yhtälö on ’epälineaarinen’, johon liittyy voimia ja johdannaistuotteita, on koodattu matemaattinen vihje saippuaelokuvien yllättävälle käyttäytymiselle. Tämä on vastakohta tutummille lineaarisille osittaisdifferentiaaliyhtälöille, kuten lämpöyhtälölle, aaltoyhtälölle ja kvanttifysiikan Schrödingerin yhtälölle.”