uveďte čísla oddělená čárkou pro výpočet.

Statistiky Týkající se Kalkulačka | Standard Deviation Calculator | Velikost Vzorku Kalkulačka

slovo znamená, což je homonymum pro více jiných slov v anglickém jazyce, je podobně dvojznačný, dokonce i v oblasti matematiky. V závislosti na kontextu, ať už matematickém nebo statistickém, se mění to, co se rozumí pod pojmem „střední“. Ve své nejjednodušší matematické definici týkající se datových sad je použitý průměr aritmetický průměr, označovaný také jako matematické očekávání nebo průměr. V této podobě znamená průměr střední hodnotu mezi diskrétní sadou čísel, jmenovitě součet všech hodnot v datové sadě, děleno celkovým počtem hodnot. Rovnice pro výpočet aritmetického průměru je prakticky totožná s rovnicí pro výpočet statistických pojmů průměr populace a vzorku, s malými odchylkami použitých proměnných:

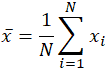
průměr je často označován jako x, vyslovuje se „x bar,“ a dokonce i v jiné účely, pokud proměnná není x, bar zápis je společný ukazatel nějakou formu říct. V konkrétním případě populačního průměru se spíše než pomocí proměnné x používá řecký symbol mu nebo μ. Podobně, nebo spíše matoucí, je průměr vzorku ve statistice často označen velkým X. Vzhledem k sadě dat 10, 2, 38, 23, 38, 23, 21, použití součtu výše výnosů:

Jak již bylo zmíněno, je to jedna z nejjednodušších definic říct, a některé další patří vážený aritmetický průměr (které se liší pouze v tom, že určité hodnoty v datové sadě přispět větší hodnotu než ostatní), a geometrický průměr. Správné pochopení daných situací a kontextů může často poskytnout osobě nástroje potřebné k určení toho, jakou statisticky relevantní metodu použít. Obecně platí, že průměr, medián, režim a rozsah by měl v ideálním případě být počítány a analyzovány na daném vzorku nebo soubor dat, protože se objasnit různé aspekty daného data, a pokud se to považuje sama, může vést ke zkreslování údajů, jak bude ukázáno v následující části.

medián

statistický koncept mediánu je hodnota, která rozděluje vzorek dat, populaci nebo rozdělení pravděpodobnosti na dvě poloviny. Nalezení mediánu v podstatě zahrnuje nalezení hodnoty ve vzorku dat, který má fyzické umístění mezi zbytkem čísel. Všimněte si, že při výpočtu mediánu konečného seznamu čísel je důležité pořadí vzorků dat. Obvykle jsou hodnoty uvedeny ve vzestupném pořadí, ale neexistuje žádný skutečný důvod, proč by seznam hodnot v sestupném pořadí poskytoval různé výsledky. V případě, že celkový počet hodnot ve vzorku dat je lichý, medián je jednoduše číslo uprostřed seznamu všech hodnot. Pokud vzorek dat obsahuje sudý počet hodnot, medián je průměr dvou středních hodnot. I když to může být matoucí, stačí si uvědomit, že i když medián někdy zahrnuje výpočet na mysli, když tento případ nastane, bude zahrnovat pouze dvě střední hodnoty, zatímco průměrný zahrnuje všechny hodnoty v datovém vzorku. V lichých případech, kdy existují pouze dva vzorky dat nebo je sudý počet vzorků, kde jsou všechny hodnoty stejné, bude průměr a medián stejné. Vzhledem ke stejné datové sady jako předtím, medián by být získány následujícím způsobem:

2,10,21,23,23,38,38

Po zápisu data ve vzestupném pořadí, a určení, že existuje lichý počet hodnot, je jasné, že 23 je medián daného případu. Pokud do datové sady byla přidána další hodnota:

2,10,21,23,23,38,38,1027892

protože existuje sudý počet hodnot, medián bude průměrem dvou středních čísel, v tomto případě 23 a 23, jejichž průměr je 23. Všimněte si, že v tomto konkrétním souboru dat, přidání odlehlá hodnota (hodnota mimo očekávaný rozsah hodnot), hodnota 1,027,892, nemá žádný skutečný vliv na datovou sadu. Pokud je však průměr vypočítán pro tuto datovou sadu, výsledek je 128,505. 875. Tato hodnota zjevně není dobrým znázorněním sedmi dalších hodnot v datové sadě, které jsou mnohem menší a blíže než průměr a odlehlé hodnoty. To je hlavní výhoda použití mediánu při popisu statistických údajů ve srovnání s průměrem. Zatímco oba, stejně jako další statistické hodnoty, by měla být vypočtena při popisu dat, pokud pouze jeden může být použit, medián může poskytnout lepší odhad typické hodnoty v daném souboru dat, kdy existují velmi velké rozdíly mezi hodnotami.

režim

ve statistice je režim hodnotou v datové sadě, která má nejvyšší počet opakování. Je možné, aby datová sada byla multimodální, což znamená, že má více než jeden režim. Například:

2,10,21,23,23,38,38

oba 23 a 38 se objeví dvakrát každý, což je oba režim pro datovou sadu výše.

podobně jako průměr a medián se režim používá jako způsob vyjádření informací o náhodných proměnných a populacích. Na rozdíl od střední a střední však, režim je koncept, který lze použít na non-číselné hodnoty, jako je značka tortilla chipsy nejčastěji zakoupené v obchodě s potravinami. Například při porovnávání značek Tostitos, Mise, a XOCHiTL, pokud je zjištěno, že v prodeji tortilla chipsy, XOCHiTL je režim a prodává se v 3:poměr 2:1 ve srovnání s Tostitos a Poslání značky tortilla chipsy, respektive, poměr by mohly být použity k určení, jak mnoho pytlů každé značky na skladě. V případě, že se v daném období prodá 24 sáčků tortilla chips, obchod by měl skladovat 12 sáčků Xochitl chips, 8 Tostitos a 4 mise, pokud používáte režim. Pokud však obchod jednoduše použil průměr a prodal 8 tašky každého, mohlo by to potenciálně ztratit 4 prodeje, pokud si zákazník přál pouze Xochitl čipy a ne jinou značku. Jak je zřejmé z tohoto příkladu, je důležité vzít v úvahu všechny způsoby statistických hodnot při pokusu o vyvození závěrů o jakémkoli vzorku dat.

rozsah

rozsah datové sady ve statistice je rozdíl mezi největší a nejmenší hodnotou. Zatímco rozsah má různé významy v různých oblastech statistiky a matematiky, toto je jeho nejzákladnější definice, a je to, co používá poskytnutá kalkulačka. Použití stejného příkladu:

2,10,21,23,23,38,38
38-2 = 36

rozsah v tomto příkladu je 36. Podobně jako průměr může být rozsah významně ovlivněn extrémně velkými nebo malými hodnotami. Použití stejného příkladu jako dříve: