Articles

Snadné Permutací a Kombinací

by admin

vždycky jsem zmatený „permutace“ a „kombinace“ — který je který?

zde je snadný způsob, jak si pamatovat: permutace zní komplikovaně,že? A je. S permutacemi záleží na každém malém detailu. Alice, Bob a Charlie se liší od Charlie, Bob a Alice (zde vložte jména svých přátel).

kombinace, na druhou stranu, jsou docela snadné. Na detailech nezáleží. Alice, Bob a Charlie jsou stejní jako Charlie, Bob a Alice.

permutace jsou pro seznamy (pořadí záleží) a kombinace jsou pro skupiny(pořadí nezáleží).

víte, „kombinační zámek“ by se měl opravdu nazývat „permutační zámek“. Pořadí, ve kterém jste vložili čísla.

snadné Permutace a kombinace

skutečný „kombinační zámek“ by akceptoval jak 10-17-23, tak 23-17-10 jako správný.

permutace: chlupaté detaily

začněme permutacemi nebo všemi možnými způsoby, jak něco udělat. Používáme fancy-pants termín „permutace“, takže se budeme starat o každý poslední detail, včetně pořadí každé položky. Řekněme, že máme 8 lidí:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

kolika způsoby můžeme udělit 1., 2. a 3. místo cena mezi osmi soutěžících? (Zlato / Stříbro / Bronz)

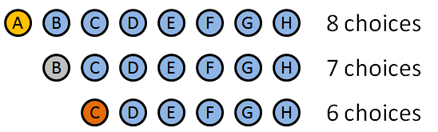
permuation příklad medailí

Budeme používat permutace od objednávky budeme rozdávat tyto medaile věcech. Zde je návod, jak se to rozpadá:

  • Zlatá medaile: 8 volby: a B C D E F G H (chytrý, jak jsem udělal jména zápas s písmeny, eh?). Řekněme, že A vyhraje zlato.
  • stříbrná medaile: 7 volby: B C D E F G H. Řekněme, že B vyhraje stříbro.
  • bronzová medaile: 6 volby: C D E F G H. řekněme… C vyhrává bronz.

vybrali jsme určité lidi, aby vyhráli, ale na detailech nezáleží: nejprve jsme měli 8 možností, pak 7, pak 6. Celkový počet možností byl $8 * 7 * 6 = 336$.

podívejme se na detaily. Museli jsme objednat 3 lidi z 8. Za tímto účelem jsme začali se všemi možnostmi (8) a poté je odebrali jeden po druhém (7, pak 6), dokud nám nedošly medaile.

víme, že faktoriál je:

\displaystyle{ 8! = 8 \cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \cdot 1 }

bohužel to dělá příliš mnoho! Chceme jen $8 * 7 * 6$. Jak můžeme“ zastavit “ faktoriál na 5?

zde se permutace ochladí: všimněte si, jak se chceme zbavit $5 * 4 * 3 * 2 * 1$. Jak se to jmenuje jinak? 5 faktoriál!

takže pokud uděláme 8!/5! dostaneme:

\displaystyle {\frac{8!}{5!} = \frac{8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \cdot 1}{5 \ cdot 4 \cdot 3 \ cdot 2 \cdot 1} = 8 \ cdot 7 \ cdot 6}

a proč jsme použili číslo 5? Protože to zbylo poté, co jsme vybrali 3 medaile z 8. Takže lepší způsob, jak to napsat, by byl:

\displaystyle {\frac{8!}{(8-3)!}}

kde 8!/(8-3)! je to jen fantastický způsob, jak říct „použijte první 3 čísla 8!”. Pokud máme n položek celkem a chcete vybrat k v určitém pořadí, dostaneme:

\displaystyle{\frac{n!}{(n-k)!}}

A tohle je fantazie permutace vzorec: máme n předmětů, a chcete najít řada způsobů, jak k položky lze objednat:

\displaystyle{P(n,k) = \frac{n!}{(n-k)!}}

kombinace, Ho!

kombinace jsou snadné. Na pořádku nezáleží. Můžete to smíchat a vypadá to stejně. Řekněme, že jsem laciný bruslař a nemůžu si dovolit samostatné Zlaté, stříbrné a bronzové medaile. Ve skutečnosti si mohu dovolit jen prázdné plechovky.

kolik způsobů mohu dát 3 plechovky 8 lidem?

v tomto případě nezáleží na pořadí, které vybíráme. Když dám plechovku Alice, Bobovi a pak Charliemu, je to stejné, jako když dám Charliemu, Alice a pak Bobovi. Každopádně jsou stejně zklamaní.

to vyvolává zajímavý bod — máme zde nějaké propouštění. Alice Bob Charlie = Charlie Bob Alice. Na chvíli zjistíme, kolik způsobů můžeme uspořádat 3 osoby.

No, máme 3 možnosti pro první osobu, 2 pro druhou a pouze 1 pro poslední. Takže máme $3 * 2 * 1$ Způsoby, jak znovu uspořádat 3 osoby.

počkejte chvíli … vypadá to trochu jako permutace! Podvedl jsi mě!

Opravdu jsem to udělal. Pokud máte n lidí a chcete vědět, kolik opatření existuje pro všechny z nich,je to jen n faktoriál nebo N!

takže pokud máme 3 plechovky na rozdávání, jsou 3! nebo 6 variant pro každou volbu, kterou vybereme. Pokud chceme zjistit, kolik kombinací máme, prostě vytvoříme všechny permutace a vydělíme všemi redundancemi. V našem případě dostaneme 336 permutací (shora) a vydělíme 6 redundancí pro každou permutaci a dostaneme 336/6 = 56.

obecný vzorec je

\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}

což znamená “ najít všechny způsoby, jak vybrat K lidi z n, a vydělte k! varianta”. Psaní tohoto, dostaneme kombinaci vzorec, nebo počet způsobů, jak kombinovat k položky ze sady n:

\displaystyle{C(n,k) = \frac{n!}{(n-k)!k!}}

Někdy C(n,k) je zapsáno jako:

\displaystyle{\binom {n}{k}}

což je binomický koeficient.

několik příkladů

zde je několik příkladů kombinací (na pořadí nezáleží) z permutací (na pořadí záleží).

  • kombinace: výběr týmu 3 lidí ze skupiny 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    permutace: výběr prezidenta, VP a Waterboy ze skupiny 10. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • kombinace: výběr 3 dezertů z nabídky 10. C (10,3) = 120.

    permutace: seznam vašich 3 oblíbených dezertů v pořadí z nabídky 10. P (10,3) = 720.

nezapamatujte si vzorce, pochopte, proč fungují. Kombinace zní jednodušší než permutace a jsou. Máte méně kombinací než permutací.

Další Příspěvky V Této Sérii

  1. Snadné Permutací a Kombinací
  2. procházení Sítě Pomocí Kombinací A Permutací
  3. Jak Chápat Kombinace Pomocí Násobení
  4. Proč musíme násobit kombinací?