Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Úvod
Náměstí kořeny jsou většinou psány pomocí odmocninou, jako je tento, ![]() . Existuje však i jiný způsob, jak reprezentovat zakořenění. Místo radikálu můžete použít racionální exponenty. Racionální exponent je exponent, který je zlomkem. Například
. Existuje však i jiný způsob, jak reprezentovat zakořenění. Místo radikálu můžete použít racionální exponenty. Racionální exponent je exponent, který je zlomkem. Například ![]() lze zapsat jako
lze zapsat jako ![]() .
.
Nedovedete si představit zvýšení čísla na racionální exponent? Může být těžké si na ně zvyknout, ale racionální exponenti mohou skutečně pomoci zjednodušit některé problémy. Pojďme prozkoumat vztah mezi racionálními (zlomkovými) exponenty a radikály.
Přepisování Radikální Výrazy Pomocí Racionální Exponenty
Radikálů a zlomkové exponenty jsou alternativní způsoby, jak vyjádřit stejnou věc. Už jste viděli, jak mohou být odmocniny vyjádřeny jako exponent k síle jedné poloviny.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Pamatovat, cubing číslo zvyšuje to na sílu tří. Všimněte si, že v těchto příkladech je jmenovatelem racionálního exponentu číslo 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and racionální exponenty: jmenovitě, že n-tý kořen čísla může být zapsán jako ![]() nebo
nebo ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an výraz obsahující racionální exponent, můžete jej přepsat pomocí radikálu. Ve výše uvedené tabulce si všimněte, jak jmenovatel racionálního exponentu určuje index kořene. Takže, exponentem ![]() znamená odmocnina, mocnina
znamená odmocnina, mocnina ![]() překládá na pátou root nebo
překládá na pátou root nebo ![]()
![]() překládá na osmou root nebo
překládá na osmou root nebo ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
Přepsat výraz s frakční exponent jako radikální. Jmenovatel zlomku určuje kořen, v tomto případě kořen krychle. závorky v |
|
|
Odpovědět |
|
|
Pamatujte si, že exponenty týkají pouze množství, okamžitě po jejich levici, pokud seskupení symbol je používán. Níže uvedený příklad vypadá velmi podobně jako předchozí příklad s jedním důležitým rozdílem-neexistují žádné závorky! Podívej, co se stane.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Jmenovatel zlomku určuje kořen, v tomto případě kořen krychle. exponent odkazuje pouze na část výrazu bezprostředně vlevo od exponentu, v tomto případě x, ale ne 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. V tomto případě je index radikálu 3, takže racionální exponent bude protože 4 je mimo radikál, není zahrnut do symbolu seskupení a exponent se na něj nevztahuje. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
Odpovědět |
|
|
Racionální Exponenty s Čitatele Jiných než Jeden
Všechny čitatele za zlomkové exponenty v příkladech výše byly 1. K vyjádření kořenů můžete použít zlomkové exponenty, které mají jiné čitatele než 1, Jak je uvedeno níže. Všimněte si nějaké vzory v této tabulce?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
přepsat radikální pomocí frakční exponent, výkon, na který radicand je zvýšena stává čitatel a kořen se stává jmenovatel.
Psaní Zlomkové Exponenty
Žádné radikální v podobě ![]() může být zapsána pomocí frakční exponent ve tvaru
může být zapsána pomocí frakční exponent ve tvaru ![]() .
.
vztah mezi ![]()
![]() pracuje pro racionální exponenty, které mají čitatel 1 stejně. Například radikální
pracuje pro racionální exponenty, které mají čitatel 1 stejně. Například radikální ![]() můžeme také zapsat jako
můžeme také zapsat jako ![]() , protože každé číslo zůstává stejné hodnoty, pokud je zvednuté na první silou. Nyní můžete vidět, odkud čitatel 1 pochází v ekvivalentní formě
, protože každé číslo zůstává stejné hodnoty, pokud je zvednuté na první silou. Nyní můžete vidět, odkud čitatel 1 pochází v ekvivalentní formě ![]() .
.
Radikální Zjednodušení Výrazů Pomocí Racionální Exponenty a Zákony Exponenty
Pojďme prozkoumat některé radikální výrazy a uvidíte, jak je zjednodušit. Zde je radikální výraz, který potřebuje zjednodušit, ![]() .
.
jednou z metod zjednodušení tohoto výrazu je faktor a vytažení skupin a3, jak je uvedeno níže v tomto příkladu.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Odpovědět |
|
|
můžete také zjednodušit tento výraz přemýšlet o radikální jako výraz s racionálním exponentem a pomocí zásady, že žádné radikální v podobě ![]() může být zapsána pomocí frakční exponent ve tvaru
může být zapsána pomocí frakční exponent ve tvaru ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
obě metody zjednodušení daly stejný výsledek, a2. V závislosti na kontextu problému může být jednodušší použít jednu nebo druhou metodu, ale prozatím si všimnete, že jste tento výraz dokázali zjednodušit rychleji pomocí racionálních exponentů než při použití metody „vytahování“.
zkusme jiný příklad.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the racionální exponent zpět k radikální formě. |
|
|
Odpovědět |
|
|
Opět platí, že alternativní metoda je v práci na zjednodušení pod odmocninou pomocí faktoringu. Pro příklad, který jste právě vyřešili, vypadá to takto.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
zkusme složitější výraz, ![]() . Tento výraz má dvě proměnné, zlomek a radikál. Vezměme si to krok za krokem a uvidíme, jestli nám použití zlomkových exponentů pomůže zjednodušit.
. Tento výraz má dvě proměnné, zlomek a radikál. Vezměme si to krok za krokem a uvidíme, jestli nám použití zlomkových exponentů pomůže zjednodušit.
začněme zjednodušením jmenovatele, protože zde se nachází radikální znaménko.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Konvencí se výraz obvykle nepovažuje za zjednodušený, pokud má ve jmenovateli zlomkový exponent nebo radikál. |
||
|
Odpovědět |
|
||
No, chvíli to trvalo, ale udělal jsi to. Použili jste to, co víte o zlomkových exponentech, negativních exponentech a pravidlech exponentů, abyste zjednodušili výraz.
Shrnutí
radikální může být vyjádřena jako výraz s frakční exponent o následující úmluvy ![]() . Přepisování radikálů pomocí zlomkových exponentů může být užitečné při zjednodušení některých radikálních výrazů. Při práci s zlomkovými exponenty nezapomeňte, že zlomkové exponenty podléhají všem stejným pravidlům jako ostatní exponenty, když se objevují v algebraických výrazech.
. Přepisování radikálů pomocí zlomkových exponentů může být užitečné při zjednodušení některých radikálních výrazů. Při práci s zlomkovými exponenty nezapomeňte, že zlomkové exponenty podléhají všem stejným pravidlům jako ostatní exponenty, když se objevují v algebraických výrazech.
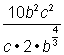
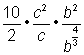
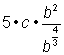
Leave a Reply