4-barevný problém je jedním z nejznámějších matematických problémů. Odolával důkazu více než sto let, než nakonec podlehl; nakonec existoval platný důkaz, ale ten, který se spoléhal na více než tisíc hodin počítačového času. Výzkum Jima Tilleyho naznačuje, že dramatické zjednodušení by nakonec mohlo být možné. Objevil se majetku, Kempe-zamykání, minimální protipříklad do 4-barevné věta musí vykazovat a formuloval domněnku, na základě rozsáhlé vyšetřování, že Birkhoff diamant je jediný zásadní Kempe-uzamčení konfigurace.

zbarvení grafu zahrnuje přiřazení štítků nebo barev vrcholům matematického objektu známého jako graf. 4-barevný problém poskytl jednu z původních motivací pro vývoj algebraické teorie grafů. Graf barvení se používá v mnoha real-svět problémy, jako je minimalizace konfliktů při plánování sportovních akcí, plánování vyšetření, řády a organizace sezení plány, i pro CCTV kamery umístění v budově s mnoha rohy, aby se minimalizovalo fotoaparát překrývají. Poskytuje také základ pro Sudoku.

4-colour problém
Francis Guthrie, student slavný Britský matematik a logik Augustus De Morgan, představuje 4-barevný problém v roce 1852. Byl formulován problém, pokud jde o mapy, které splňují určité podmínky, jako neobsahující žádné díry, a že každá oblast (např. země nebo stát) spojeny tak, že žádný region, existuje ve dvou nebo více nesouvislých částí. Guthrie tvrdí, že pro takové mapy, že by nikdy trvat více než čtyři barvy na obarvení mapy tak, aby žádné dva sousední regiony, byly stejné barvy.

v dnešní době je 4-barevný problém vyjádřen v grafech a místo vybarvení oblastí v Mapách jeden vybarví vrcholy v grafech. Všechny existující důkazy 4-barevné věty ukazují, že minimální protipříklad nemůže existovat. (Minimální protipříklad je nejmenší rovinný graf, který vyžaduje více než čtyři barvy pro správné zbarvení jeho vrcholů.) Pouze rovinné grafy, které jsou triangulace, je třeba zvážit, jako každý graf, který není triangulace může být otočen do jednoho vložením hrany. Pokud je výsledná triangulace 4barevná, pak je původní graf také 4barevný. Je velmi užitečné mít možnost omezit kontrolu na triangulace.

rané pokus na důkaz
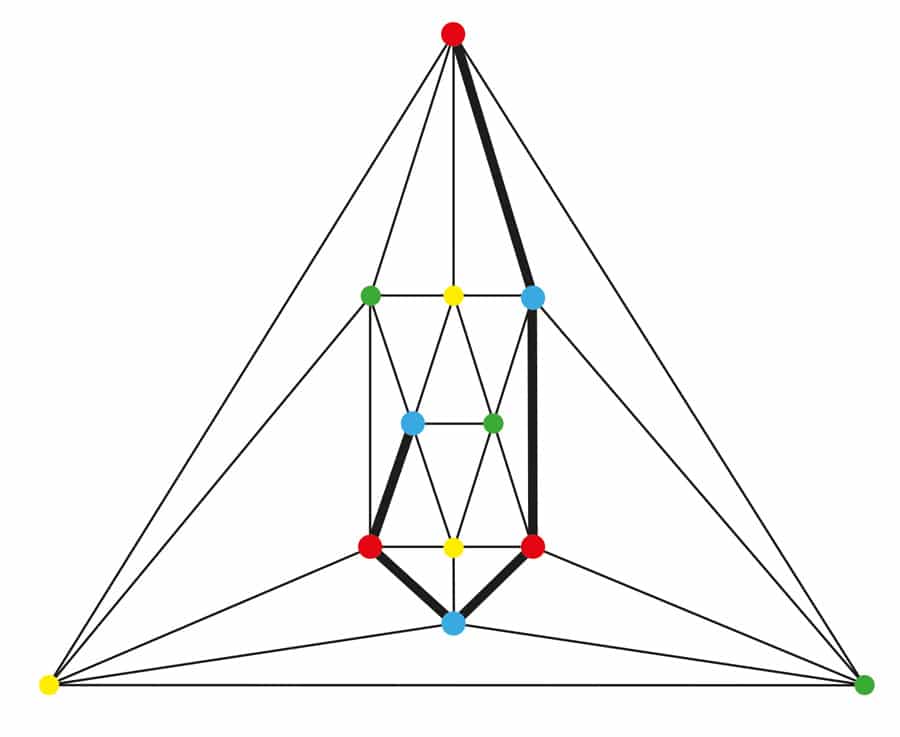
Z těch, kdo podává důkaz, Alfred Bray Kempe, anglický právník a amatérský matematik, byl člověk, jehož pověst byla nejvíce poznamenána jeho neúspěšném úsilí. Oznámil svůj úspěch v roce 1879 a jeho „důkaz“ byl publikován v American Journal of Mathematics. O jedenáct let později, nicméně, další anglický matematik, Percy Heawood, vytvořil mapu, že on 4-barevné až do konečného regionu takovým způsobem, že Kempe metoda selhala na to konečné regionu. Přes jeho selhání zanechal Kempe užitečný nástroj-řetězec Kempe. Je to maximální, propojený (každý vrchol dosažitelný z jakéhokoli jiného cestou podél okrajů) podgraf, ve kterém všechny vrcholy používají přesně dvě barvy. Řetězce Kempe se osvědčily při barvení a přebarvení grafů. Viz Obrázek 1.

bylo by ohromujícím zjednodušením
, kdyby samotný diamant Birkhoff byl klíčem k 4-colourrability.

důkaz konečně
První platný důkaz byl oznámen v roce 1976 Kennethem Appelem a Wolfgangem Hakenem. K ověření konkrétních aspektů jejich argumentace vyžadovalo přes tisíc hodin počítačového času. Tento pojem spoléhání se na počítačový kód, potenciálně obsahující chyby vyvolané člověkem (a jejich kód Ano!), spíše než „lidský“ důkaz, neuspokojil velkou část matematické komunity. Důkaz appela a Hakena byl elegantní ve své celkové struktuře, ale detaily byly ošklivé.

důkaz byl vylepšen v roce 1996 týmem čtyř matematiků: Robertson, Sanders, Seymour a Thomas, ale stále se spoléhali na počítačový kód, aby dokončili svůj důkaz. V roce 2010 Steinberger nabídl další variantu. Stále však neexistuje zcela uspokojivá odpověď, proč je 4-barevná věta pravdivá. (Jakmile byla domněnka prokázána, získala status ‚ věty.‘)

hledat alternativní důkaz
4-colour problém je tak snadné, formulovat a pochopit, že to přilákalo pozornost mnoha tisíců amatérských matematici, všichni věří, že mohou najít jednoduchý, klasický důkaz, a tak se stal slavným. Otec Jima Tilleyho, fyzik a ředitel kanadské Royal Military College v letech 1978-1984, byl jedním z takových snílků. Kdykoli cítil, že udělal průlom, požádal svého syna Jima, aby zkontroloval jeho práci. Jim vždycky našel chybu. Přesto, navzdory počáteční skepsi, že úsilí jeho otce někdy přinese ovoce, nakazil se nadšením pro 4-barevný problém a začal ho intenzivně studovat.

Kempe-locking
výzkum Jima Tilleyho vedl k jeho objevení nové vlastnosti, kterou musí vykazovat minimální protipříklad 4-barevné věty. Pojmenoval to Kempe-locking. Uvědomil si, že je pravděpodobně neslučitelná s jinou vlastností, kterou musí vykazovat minimální protipříklad-viz., jak je graf připojen (kolik vrcholů musí být z grafu odstraněno, než se rozpadne).

Tilley ‚ s Kempe-locking je vlastnost spojená s hranou v triangulaci. Pojem začíná odstraněním hrany xy mezi sousedními vrcholy x a y. Pokud pro každé 4-barvení výsledný graf, ve kterém barvy x a y jsou stejné, tam je žádné pořadí barev-uzlů na Kempe řetězy, které způsobí, že barva x se liší od barvy y, pak původní triangulace je řekl, aby byl Kempe-zamčené s ohledem na okraji xy. Tilley dokázal, že minimální protipříklad 4-barevné věty musí být Kempe uzamčen s ohledem na každý z jeho okrajů; každá hrana v minimálním protipříkladu musí mít tuto barvicí vlastnost.

Kempe-locking je obzvláště omezující podmínka, která se stává obtížnější splnit, jak se triangulace zvětšuje. Tilley se rozhodl zjistit, zda existuje něco společného s triangulacemi, které mají Kempe uzamčené hrany. Jeho nejstarší hledání Kempe-zamykání ho vedlo k Birkhoff diamantu.

Birkhoff diamond
V roce 1913, G. D. Birkhoff zjistil, že určité konfigurace deset zemí v mapě (hranice kruhu šesti zemí, které obklopuje sada čtyř zemí) má důležitou vlastnost. Pokud je tato konfigurace přítomna v mapě a pokud je podkapela s odstraněnou konfigurací 4-colourable, pak bude celá mapa 4-colourable. Minimální protipříklad tedy nemůže obsahovat tuto konkrétní konfiguraci. To přišlo být známý jako Birkhoff diamant. Tilley zjistil, že Kempe-locked edge xy zdá se, že vznikají pouze tehdy, když x a y jsou také koncové body grafové verze Birkhoff diamantu. Viz Obrázek 2.

domněnka je snadno uvedena, srozumitelná a zajímavá a nabízí přesvědčivé vysvětlení, proč jsou všechny rovinné grafy 4-barevné.

kteří se setkali s jakýmkoli Kempe-uzamčení konfigurace bez Birkhoff diamond, on se domníval, že Birkhoff diamant je pouze „základní“ Kempe-uzamčení konfigurace, která neobsahuje menší Kempe-uzamčení konfigurace jako podgraf. Tilley však zjistil, že nemůže prokázat své kritické domněnky. Bylo to frustrující, protože, pokud je to pravda, domněnka by přímo dokázala 4-barevnou větu. (Minimální protipříklad, triangulace by měl obsahovat Birkhoff diamond podgraf, ale pokud ano, to nemohl být minimální protipříklad.)

drtivá podpora případ
místo toho, aby prokázal své domněnky, Tilley udělal další nejlepší věc. On se rozhodl hrát roli experimentátor a vybudovat ohromující případě na podporu jeho dohad. On rozdělil všechny příslušné rovinné triangulace do dvou tříd: na ty, v nichž alespoň čtyři vrcholy musí být odstraněny před grafy rozpadne (4-connected) a ty, v nichž alespoň pět vrcholů, musí být odstraněny před grafy rozpadne (5-připojen). Viz Obrázek 3. Užitečné v Tilley rozsáhlé pátrání bylo, že musel zkoumat pouze jeden člen z každého izomorfismus třídy (grafů, které jsou strukturálně identické). Tilley zkoumal všechny 8,044 izomorfismus třídy 4-připojen planární triangulace až na 15 vrcholech a všechny 9,733 izomorfismus třídy 5-připojen planární triangulace až na 24 vrcholů. Našel jen tři Kempe-zamčené triangulace. Každý objevený Kempe uzamčený okraj představoval Birkhoffův diamant a každý se objevil ve 4-připojené triangulaci. Mezi 5-spojenými triangulacemi nebyly vůbec žádné.

Tilley rozšířil jeho hledání mezi 4-připojen triangulace tím, že zkoumá všechny 30,926 izomorfismus tříd na 16 vrcholů a všechny 158,428 izomorfismus tříd na 17 vrcholech. Výpočet-časová omezení znamenala omezení jeho vyhledávání na vzorky 100 000 náhodně generovaných neizomorfních triangulací pro třídy na 18,19 a 20 vrcholech. Rozšířené vyhledávání se obrátil až 45 další Kempe-zamčené triangulace, ale přesně stejné výsledky jako původní hledání: každý Kempe-zamčené hrany v triangulaci představoval spojené Birkhoff diamant.

odkud?
Tilleyho rozsáhlé vyhledávání snadno potvrdilo, že Birkhoffův diamant je základní konfigurací zamykání Kempe. Důkladně otestoval své domněnky, ale zůstává neprokázané. Pokud (nebo když) Tilleyho je domněnka se ukázala jako pravdivá, tzn., že Birkhoff diamond, sám je klíčem k 4-colourability, bylo by to úžasné zjednodušení problému: jednou konfigurací, která to vše vysvětluje – matematické elegance.

prokázání 4-barevné domněnky vyžadovalo úsilí mnoha významných matematiků. Tilleyho domněnka, že Birkhoffův diamant je jedinou základní konfigurací zamykání Kempe, může být ještě obtížnější prokázat. Experimentální důkazy jsou však silné. Teoretici by mohli říci: „proč se obtěžovat?’Tilley odpověď je, že neukojitelná zvědavost zvítězí: „Po tom všem, dohad je, jednoduše řečeno, je pochopitelné, a zajímavé, a nabízí přesvědčivé vysvětlení pro to, proč všechny rovinné grafy jsou 4-colourable.“