Matematika je spíš maraton než sprint — je to dlouhý, pomalý a stabilní mletí, s vzácné okamžiky průlom. Přesto, jednou za čas, dostaneme ty ceněné momenty „Eureka“, ty krátké řádky písmen a čísel, které navždy mění vědu. Zde jsou některé z nejznámějších rovnic, od starověkých Řeků po moderní fyziku.

Pythagora věta (530 PŘ.)

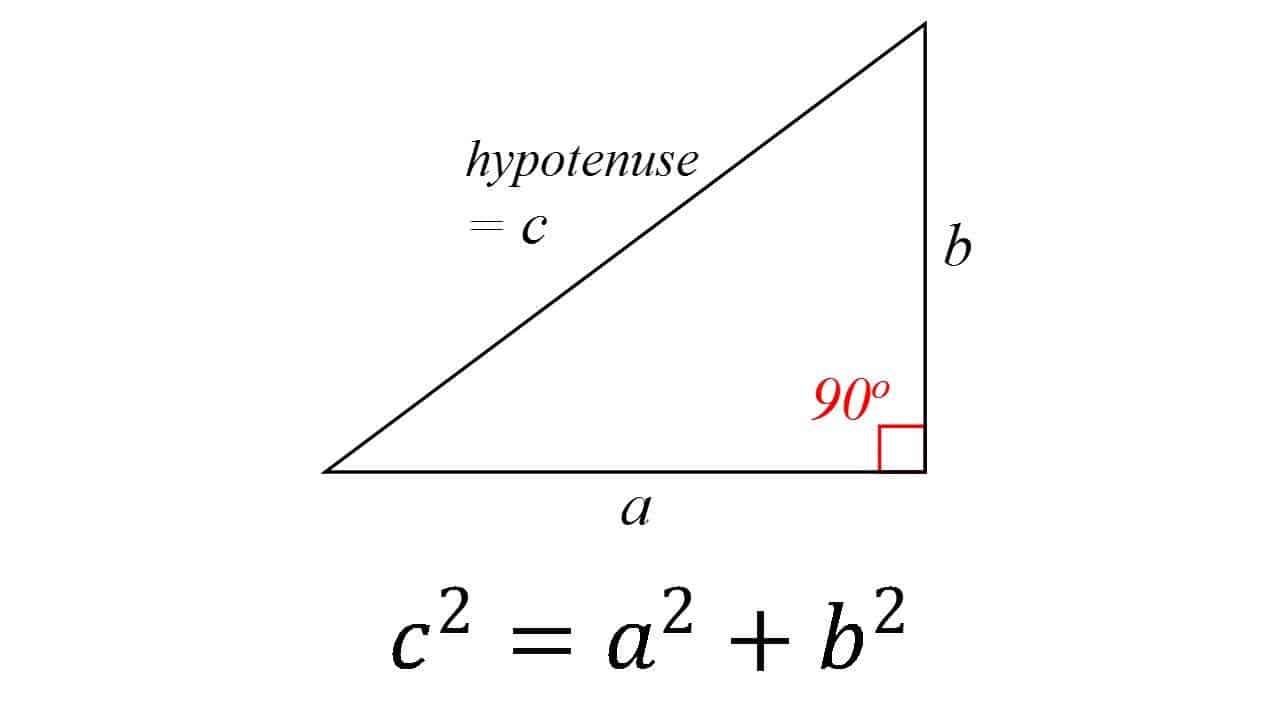
To je opravdu jeden z foundating pilířů všechny geometrie: v pravoúhlém trojúhelníku se čtverec přepony (strana opačná k pravému úhlu)rovná součtu čtverců ostatních dvou. Teorie je obecně připisována řeckému matematikovi Pythagorovi, ačkoli existují důkazy, že babylonští matematici pochopili vzorec. Je také velmi možné, že věta byla známa mnoha lidmi,ale on byl první, kdo to dokázal.

věta byla dána četnými důkazy-možná nejvíce pro jakoukoli matematickou větu. Jsou velmi rozmanité, včetně geometrických důkazů a algebraických důkazů, s některými chodit s někým zpět tisíce let.

Komplexní čísla

italský matematik Gerolamo Cardano je první známo, že mají zavedena komplexní čísla, volat je „fiktivní“ v té době. Nicméně, matematický vývoj „já“ jako imaginární číslo představující odmocnina z -1 je přičítán Leonhard Euler, jeden z nejvýznamnějších matematiků a vědců v historii lidstva.

komplexní čísla jsou v podstatě čísla, která ve skutečnosti neexistují, ale která jsou velmi užitečná pro řadu výpočtů. Skládají se z čísla s reálnou část (čísla všichni víme) a imaginární část (zastupoval jsem zde) a mají praktické aplikace v řadě oborů, včetně fyziky, chemie, biologie, ekonomie, elektrotechnika a statistiky.

logaritmu

Logaritmů jsou v podstatě inverzní funkce umocňování. Budete potřebovat číslo (N), base (a), a logaritmus N při základu a bude x, kde N se rovná síle x. To se může zdát jako jen jiný způsob, jak psát to samé (a v jistém smyslu je), ale logaritmy mají nesčetné množství praktických aplikací, se používá v psychologii, ekonomiku, a měření mnoha fyzikálních jevů (jako je pH nebo zemětřesení magnitudy).

logaritmy veřejně navrhl John Napier v roce 1614 v knize s názvem Mirifici Logarithmorum Canonis Descriptio (popis nádherného pravidla logaritmů) — vhodný název. Zvláštním případem logaritmu je přirozený logaritmus-e, kde e je iracionální a transcendentální číslo přibližně rovné 2,71828182845. Ve skutečnosti má e sama o sobě fascinující historii a působivý počet aplikací, ale to je příběh pro jinou dobu.

Počet

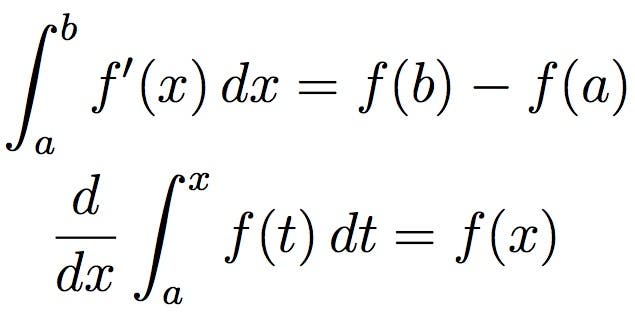
několik oblastí matematiky bylo stejně působivých jako počet. Vyvinutý v 17. století Isaacem Newtonem a Gottfriedem Wilhelmem Leibnizem, počet je široce používán ve vědě, inženýrství, a ekonomie. Počet se obvykle zaměřuje na řešení malých veličin, zejména nekonečně malých veličin. Prostřednictvím počtu lze s nimi zacházet jako s reálnými čísly, i když jsou technicky nekonečně malá.

pro jednodušší vizualizaci lze integraci znázorněnou výše považovat za měření plochy pod křivkou definovanou funkcí.

Zákon Gravitace

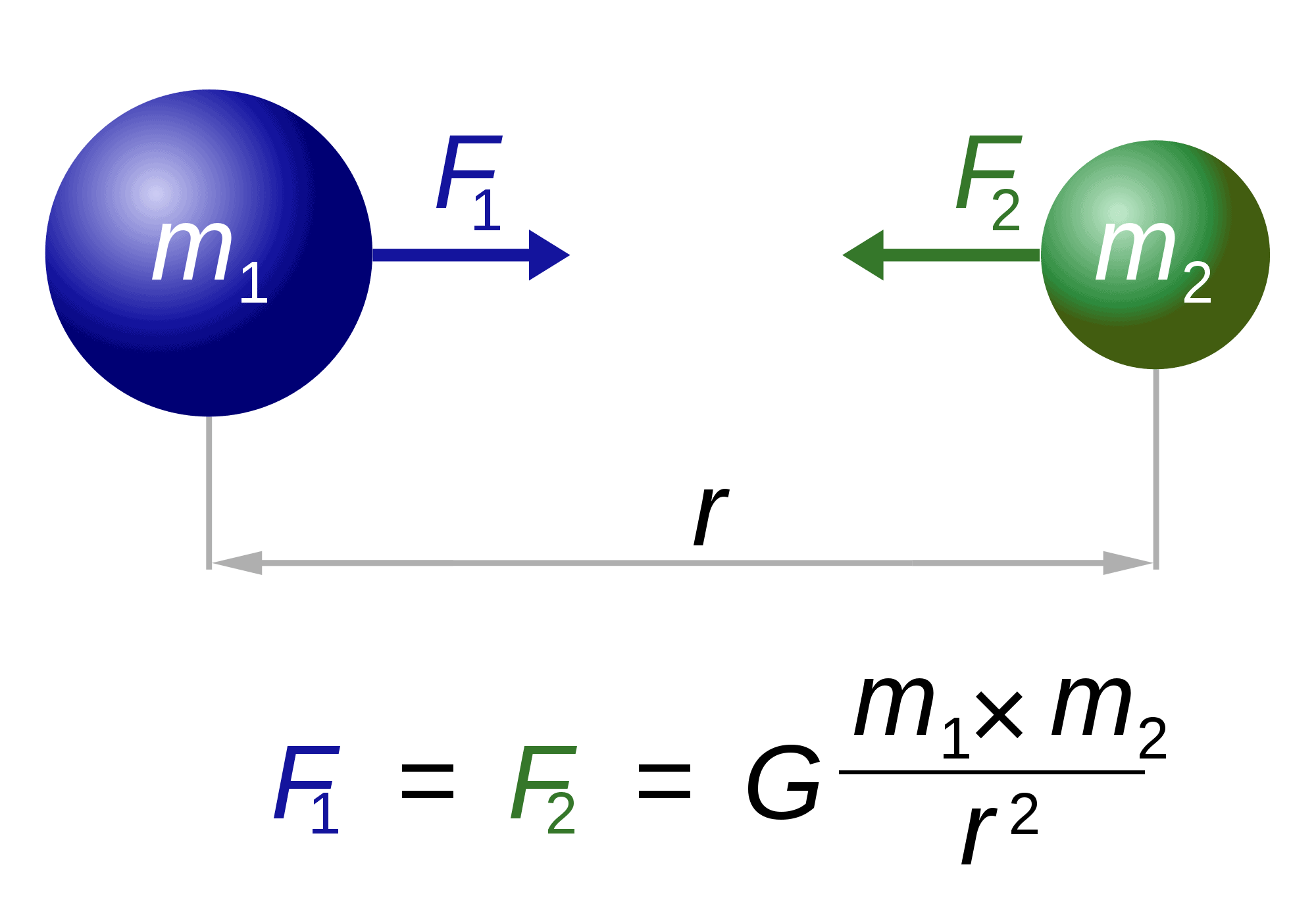
když už Mluvíme o Newtonech, je to také „zodpovědný“ za jeden z světa je nejvíce slavné a velkolepé rovnice: gravitační zákon.

zákon v podstatě popisuje, jak jsou k sobě přitahována jakákoli dvě tělesa M1 a m2. Síla (F1, F2) je nepřímo úměrná čtverci vzdálenosti mezi nimi (r). Jediným zbývajícím faktorem, G, je gravitační konstanta. Povaha této konstanty zůstává nepolapitelná.

obecná relativita

téměř 200 let Newtonův zákon definoval naši úroveň porozumění mechanice. Einsteinova práce ve 20. století vzali věci na další úroveň — tyto dva úspěchy věž na nejvyšší podstavce ve světě fyziky.

Obecné teorie relativity je v podstatě geometrická teorie gravitace, zobecnění Newtonova teorie poskytuje jednotný popis gravitace jako geometrické vlastnosti prostoru a času — nebo časoprostoru. Zejména, Einstein ukázal, nejen, že tam je takový věc jako „časoprostor“ sloučení tří rozměrů s 4. dimenze času, ale on také ukázal, že tento časoprostor může být zakřiven gravitací, s zakřivení je přímo úměrná energii a hybnost, co hmota a záření jsou přítomny.

Druhý zákon termodynamiky

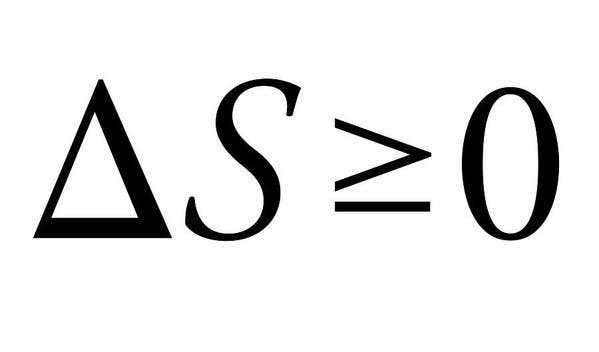
Druhý Zákon Termodynamiky je důvod, proč nemůžeme mít hezké věci ve Vesmíru. Vtipy stranou, čtyři zákony termodynamiky definovat základní fyzikální veličiny (teplota, energie a entropie), které charakterizují termodynamické systémy. Zejména druhá zde vyniká svou jednoduchostí, ale naprosto masivními důsledky.

zákon v podstatě říká, že součet entropií interagujících termodynamických systémů se musí vždy zvyšovat nebo nanejvýš zůstat konstantní. Když se energie mění z jedné formy na druhou nebo se hmota pohybuje kolem, entropie (nebo porucha) v uzavřeném systému se zvyšuje. Všechny rozdíly v teplotě, tlaku a hustotě mají tendenci naplno po chvíli

Maxwellovy Rovnice

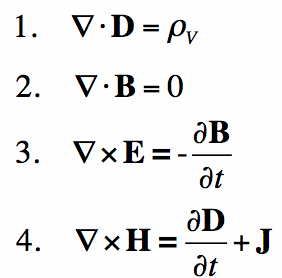
Jednoduše řečeno, Maxwell ‚ s rovnice pro elektromagnetismus, co Newtonova zákona je mechanika. Poskytují matematický základ pro klasický elektromagnetismus, klasickou optiku a elektrické obvody. Jsou široce používány v samotném zařízení, na kterém čtete — v podstatě všechna elektronická zařízení.

Maxwellovy zákony popisují, jak jsou elektrická a magnetická pole generována náboji, proudy a změnami polí. Významným průlomem byla demonstrace, že elektrické a magnetické pole se šíří rychlostí světla.

Eulerovu Identitu

a Konečně, a to je dost možná nejelegantnější rovnice, věc nejvyšší krásu, protože to zahrnuje všechny „základní“ čísla:

• 0, která je neutrální pro sčítání a odčítání;
• 1, které je neutrální k násobení a dělení;
• e, což je Eulerovo číslo (viz výše), základ přirozeného logaritmu;
• i je imaginární jednotka (viz výše); a
• π je pi, poměr obvodu kruhu k jeho průměru.

nalezení vztahu, který sjednotí všechna tato čísla, není nic dechberoucího a zdá se docela nepravděpodobné. Demonstrace není úplně jednoduchá, ale můžete ji vidět zde.

je To jen příznačné, že Stanford University profesor matematiky Keith Devlin popsané rovnice, říká, že „jako Shakespearovský sonet, který zachycuje podstatu lásky, nebo obraz, které přináší krásu lidské formě, která je daleko více než jen kůže, hluboké, Eulerova rovnice dosáhne dolů do hlubin existence“

To není často, že matematika a fyzika se redukuje na jednoduchá a elegantní rovnice, ale když oni dělají, je to docela radost pohledět.