síla může být myšlenka jako push orpull v určitém směru. Když je síla aplikována na objekt,výsledný pohyb objektu závisí na tom, kde je aplikována síla a jak je objekt omezen.Pokud je objekt nekonfinovaný a síla je aplikována prostřednictvímcentrum gravitace, objekt se pohybuje čistě, jak popisuje Newtonův pohyb.Pokud je objekt omezen (nebo připnut) na nějakém místě zvaném apivot, objekt je o otočném čepu, ale nepřekládá se.Síla je přenášena otočným čepema detaily otáčení závisí na vzdálenosti odpoužitá síla na čep.Pokud je objekt neomezený a síla je aplikována v některýchvzdálenost od těžiště, objekt se překládá a otáčí se kolem těžiště.Podrobnosti o rotaci závisí na vzdálenosti odaplikovaná síla do těžiště.Pohyb létajících objektů je popsán tímto třetím typem pohybu; kombinace překladu a rotace.

síla F je avektorová veličina, což znamená, že má jak velikost, tak směr s ním spojený. Asměr sílyje důležitý, protože výsledný pohyb objektuje ve stejném směru jako síla.Součin síly a kolmé vzdálenosti uprostřed gravitace pro volnou objekt,nebo otočný na uzavřeném objektu, je^Mcalled točivý moment nebo moment.Točivý moment je také vektorová veličina a vytváří rotacistejným způsobem, jakým síla vytváří překlad. Konkrétně, objekt atrest, nebo rotující při konstantní úhlové rychlosti, bude pokračovat takžedokud nepodléhá vnějšímu točivému momentu. Točivý moment vytváří změnuv úhlové rychlosti, která se nazývá Úhlové zrychlení.

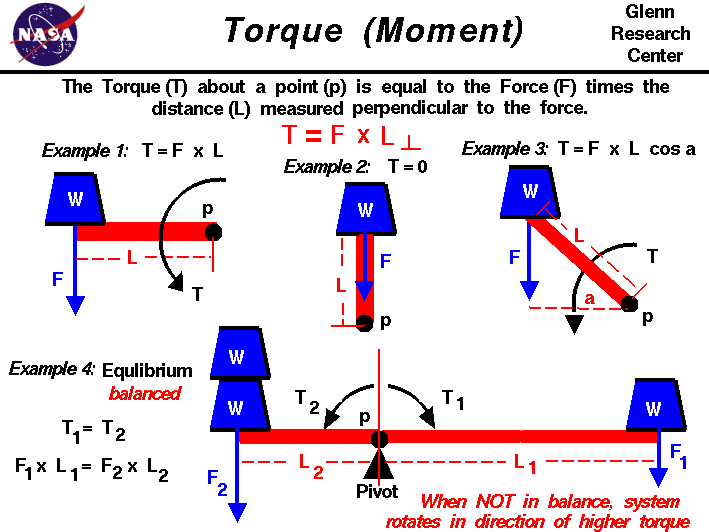
vzdálenost L použitá ke stanovení točivého momentu T je vzdálenost od p k síle, ale měřená kolmo k směru síly.Na obrázku, ukážeme čtyři příklady momenty pro ilustraci basicprinciples správní momenty.V každém příkladu modrá hmotnost W působí na červený pruh, který je calledan ruku.

v příkladu 1 je síla (hmotnost) aplikována kolmona rameno. V tomto případě je kolmá vzdálenost délkabar a točivý moment se rovná součinu délky a síly.

V Příkladu 2, stejná síla je aplikována do paže,ale síla nyní působí přímo přes thepivot. V tomto případě je vzdálenost od čepu kolmá k síleje nula. Takže v tomto případě je točivý moment také nulový.Myslete na sklopné dveře. Pokud zatlačíte na okraj dveří, směrem k pantu, dveře se nepohybujíprotože točivý moment je nulový.

příklad 3 je obecný případ, kdy je síla aplikována v určitém úhlu a na rameno. Kolmá vzdálenost je dántrigonometriejako délka ramene (L) krátkosin (cos)úhlu.Točivý moment je pak dán vztahem:

Příklady 1 a 2 může být odvozen z tohoto obecného vzorce,protože thecosine 0 stupňů 1.0 (Příklad 1), a cosinus 90 stupňů je 0.0 (Příklad 2).

v příkladu 4 byl otočný čep přesunut z konce lišty naumístění blízko středu lišty. Váhy se přidávají na obě strany pivot.To pravá jediná hmotnost W vytváří působící sílu F1 ve vzdálenosti L1 od čepu. Tím se vytvoří točivý moment T1 rovnající seprodukt síly a vzdálenosti.

vlevo od pivot dvě závaží W vytvářejí sílu F2 ve vzdálenosti L2.To vytváří točivý moment T2 ve směru opačném od T1, protože vzdálenost je v opačném směru.

Pokud byl systém v rovnováze,nebo vyvážený, momenty by být rovné a ne čistý točivý moment bude působit na systém.

Pokud systém není v rovnováze, nebo nevyvážené, bar rotatesabout otáčení ve směru vyšší točivý moment.Pokud F2 = 2 * F1, jaký je vztah mezi L1 a L2 pro vyvážení systému? Pokud F2 = 2 * F1 a L1 = L2, kterým směrem by se systém otáčel?

letečtí inženýři používají kroutící moment generovaný aerodynamickými plochami ke stabilizaci a řízení letadel.Na letadlech vytvářejí řídicí plochyaerodynamické síly.Tyto síly jsou aplikovány v určité vzdálenosti odletadla cg a protozpůsobit otáčení letadla. Theelevators produkují apitching moment, therudder produkují ayawing moment, and theailerons produkují arolling moment. Schopnost měnit množstvísíla a moment umožňuje pilotovi manévrovat nebo totrimovat Letadlo.Na modelových raketách se Finy používají k vytváření točivého momentu kolem rocketcenter of gravityto providestabilityduring powered flight.U draků jsou aerodynamické a hmotnostní silyvyrábějí točivý moment kolem bodu nevěsty.Vzdálenost od bodu uzdy a velikost sil má silný vliv navýkon draka.

aktivity:
Prohlídky

• Síly, Momenty a Pohybu:
• Základní Letadel Pohybu:
• Letadla Roll Pohybu:
• Letadla Hřiště Pohybu:
• Letadla Stáčení Pohybu:
• Křidélka:
• Spoilery:
• Výtahy:
• Stabilators:
• Kormidlo:
• Stability Modelu Rakety:

Navigace..

Začátečník Průvodce Domovskou Stránku