Purplemath

„mezikvartilové rozpětí“, zkráceně „IQR“, je jen šířka boxu v box-and-whisker plot. To znamená, že IQR = Q3 – Q1 . IQR lze použít jako měřítko toho, jak jsou hodnoty rozloženy.

Statistika předpokládá, že vaše hodnoty jsou seskupeny kolem nějaké centrální hodnoty. IQR říká, jak jsou rozloženy“ střední „hodnoty; lze jej také použít k určení, kdy jsou některé z dalších hodnot „příliš daleko“ od centrální hodnoty. Tyto“ příliš vzdálené „body se nazývají „odlehlé hodnoty“, protože“ leží mimo “ rozsah, ve kterém je očekáváme.

IQR je délka pole ve vašem grafu box-and-whisker. Odlehlá hodnota je jakákoli hodnota, která leží více než jeden a půlkrát větší než délka krabice z obou konců krabice.

Obsah Pokračuje Níže

MathHelp.com

to znamená, Že pokud datový bod je nižší než Q1 – 1.5×IQR nebo nad Q3 + 1.5×IQR, to je vnímána jako příliš daleko od střední hodnoty musí být přiměřené. Možná jste narazil na vážení měřítku, když jste dělali, že jedno měření, nebo možná, že váš partner je idiot a neměl jsi ho nechat sahat. Kdo ví? Ale bez ohledu na jejich příčinu, odlehlé hodnoty jsou ty body, které se nezdají „zapadnout“.

jakmile budete pohodlně najít IQR, můžete přejít k nalezení odlehlých hodnot, pokud existují.

• vyhledejte případné odlehlé hodnoty pro následující datovou sadu:

hodnoty pro Q1 – 1.5×IQR a Q3 + 1.5×IQR jsou „ploty“, které označují“ rozumné “ hodnoty od odlehlých hodnot. Odlehlé hodnoty leží mimo ploty.

Pokud máte za úkol zvážit nejen odlehlé hodnoty, ale také „extrémní hodnoty“, pak hodnoty pro Q1 – 1.5×IQR a Q3 + 1.5×IQR jsou“ vnitřní „ploty a hodnoty pro Q1 – 3×IQR a Q3 + 3×IQR jsou“ vnější “ ploty.

odlehlé hodnoty (označené hvězdičkami nebo otevřenými tečkami) jsou mezi vnitřním a vnějším plotem a extrémní hodnoty (označené podle toho, který symbol jste nepoužili pro odlehlé hodnoty) jsou mimo vnější ploty.

mimochodem, vaše kniha může odkazovat na hodnotu „1,5×IQR“ jako na „krok“. Pak odlehlé hodnoty budou čísla, která jsou mezi jedním a dvěma kroky z pantů, a extrémní hodnoty budou čísla, která jsou více než dva kroky z pantů.

při pohledu na předchozí příklad by vnější ploty byly 14,4-3×0,5 = 12,9 a 14,9 + 3×0,5 = 16,4. Protože 16.4 je přímo na horním vnějším plotu, bylo by to považováno pouze za odlehlou hodnotu, nikoli za extrémní hodnotu. Ale 10.2 je zcela pod spodním vnějším plotem, takže 10.2 by byla extrémní hodnota.

Vaše grafická kalkulačka, která může nebo nemusí indikovat, zda box-and-whisker plot obsahuje odlehlé hodnoty. Například výše uvedený problém zahrnuje body 10.2, 15.9 a 16.4 jako odlehlé hodnoty. Jedno nastavení na mém graphing calculator dává jednoduchý box-and-whisker plot, který využívá pouze pět-číslo shrnutí, tak nejdále odlehlé hodnoty jsou uvedeny jako koncové body vousy:

jiná nastavení kalkulačka dává box-and-whisker plot s odlehlých hodnot speciálně označena (v tomto případě, simulace otevřené tečka), a vousy jít jen tak daleko, jak nejvyšší a nejnižší hodnoty, které nejsou odlehlé hodnoty:

Moje kalkulačka nerozlišuje mezi odlehlých a extrémních hodnot. Tvoje taky nemusí. Před dalším testem si přečtěte příručku svého majitele.

Pokud používáte grafickou kalkulačku na pomoc s těmito pozemky, ujistěte se, že víte, které nastavení byste měli být pomocí a co výsledky znamenají, nebo kalkulačku, může vám dokonale správná, ale „špatné“ odpovědi.

• Najděte odlehlé hodnoty a extrémní hodnoty, pokud existují, pro následující datovou sadu a nakreslete graf box-and-whisker. Označte všechny odlehlé hodnoty hvězdičkou a jakékoli extrémní hodnoty otevřenou tečkou.

Reklama

K nalezení odlehlých a extrémních hodnot, jsem poprvé muset najít IQR. Protože tam jsou sedm v seznamu hodnoty, medián je čtvrtá hodnota, takže:

Q2 = 25,

první polovina seznamu je:

21, 23, 24,

…takže Q1 = 23, druhá polovina je:

29, 33, 49,

…tak Q3 = 33. Pak je IQR dán:

IQR = 33-23 = 10

odlehlé hodnoty budou mít níže uvedené hodnoty:

23 – 1.5×10 = 23 – 15 = 8

…nebo výše:

33 + 1.5×10 = 33 + 15 = 48

extrémní hodnoty budou ty níže:

23 – 3×10 = 23 – 30 = -7

…nebo výše:

33 + 3×10 = 33 + 30 = 63

takže mám odlehlé hodnoty na 49, ale žádné extrémní hodnoty. Nebudu mít na svém pozemku top whisker, protože Q3 je také nejvyšší odlehlá hodnota. Takže můj spiknutí vypadá takto:

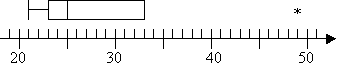
Je třeba poznamenat, že metody, podmínky a pravidla uvedená výše, jsou to, co jsem se naučil a to, co jsem nejčastěji viděl učil. Váš kurz však může mít různá specifická pravidla nebo vaše kalkulačka může provádět výpočty mírně odlišně. Možná budete muset být poněkud flexibilní při hledání odpovědí specifických pro vaše osnovy.