tutorial vysvětluje základy regresní analýzy a ukazuje několik různých způsobů, jak to udělat lineární regrese v aplikaci Excel.

Představte si toto: máte k dispozici spoustu různých údajů a jste požádáni, abyste předpovídali prodejní čísla pro vaši společnost v příštím roce. Objevili jste desítky, možná i stovky faktorů, které mohou ovlivnit čísla. Ale jak víte, které z nich jsou opravdu důležité? Spusťte regresní analýzu v aplikaci Excel. To vám dá odpověď na tuto a mnoho dalších otázek: Na kterých faktorech záleží a které lze ignorovat? Jak úzce spolu tyto faktory souvisejí? A jak si můžete být jisti předpovědí?

• Regresní analýzy v Excelu
• Lineární regrese v aplikaci Excel s Analytické nástroje
• Nakreslete lineární regrese grafu
• Regresní analýzy v Excelu se vzorci

Regresní analýzy v programu Excel – základy

Ve statistické modelování, regresní analýza se používá k odhadu vztahů mezi dvěma nebo více proměnnými:

závislá proměnná (aka proměnná kritéria) je hlavním faktorem, který se snažíte pochopit a předvídat.

nezávislé proměnné (aka vysvětlující proměnné nebo prediktory) jsou faktory, které mohou ovlivnit závislou proměnnou.

Regresní analýza vám pomůže pochopit, jak závislá proměnná se změní, když jedna z nezávislých proměnných se liší a umožňuje matematicky určit, která z těchto proměnných má opravdu vliv.

technicky je model regresní analýzy založen na součtu čtverců, což je matematický způsob, jak najít rozptyl datových bodů. Cílem modelu je získat co nejmenší součet čtverců a nakreslit čáru, která je nejblíže k datům.

ve statistikách rozlišují mezi jednoduchou a vícenásobnou lineární regresí. Jednoduché lineární regresní modely vztah mezi závislou proměnnou a jednou nezávislou proměnnou pomocí lineární funkce. Pokud k předpovědi závislé proměnné použijete dvě nebo více vysvětlujících proměnných, zabýváte se vícenásobnou lineární regresí. Pokud je závislá proměnná modelována jako nelineární funkce, protože datové vztahy nesledují přímku, použijte místo toho nelineární regresi. Tento kurz se zaměří na jednoduchou lineární regresi.

jako příklad si vezměme prodejní čísla deštníků za posledních 24 měsíců a zjistíme průměrné měsíční srážky za stejné období. Děj této informace na grafu a regresní přímky bude demonstrovat vztah mezi nezávislou proměnnou (srážky) a závislé proměnné (deštník prodeje):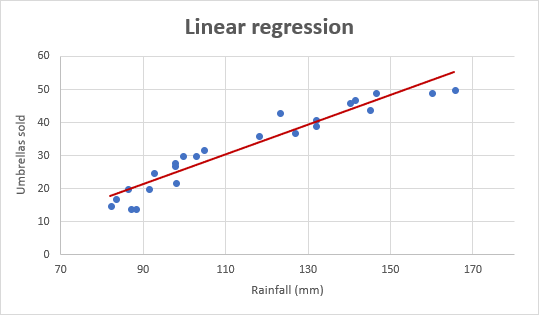

Lineární regresní rovnice

Matematicky lineární regrese je definován podle rovnice:

Kde:

• x je nezávislá proměnná.
• y je závislá proměnná.
• a je y-intercept, což je očekávaná střední hodnota y, když jsou všechny proměnné x rovny 0. Na regresním grafu je to bod, kde přímka protíná osu Y.
• b je sklon regresní přímky, což je rychlost změny pro y jako změny x.
• ε je náhodná chyba horizontu, což je rozdíl mezi skutečnou hodnotou závislé proměnné a její předpokládaná hodnota.

lineární regresní rovnice má vždy chybový termín, protože v reálném životě nejsou prediktory nikdy dokonale přesné. Některé programy, včetně Excelu, však provádějí výpočet chybového termínu v zákulisí. Tak, v aplikaci Excel, můžete udělat lineární regrese pomocí metody nejmenších čtverců a hledat koeficienty a a b tak, že:

Pro náš příklad, lineární regresní rovnice má následující tvar:

Umbrellas sold = b * rainfall + a

Existuje několik různých způsobů, jak najít a b. Tři hlavní způsoby provedení lineární regresní analýzy v Excelu, jsou:

• nástroj Regrese součástí Analytické nástroje
• Bodový graf s trendovou linií
• Lineární regrese vzorec,

Níže najdete podrobný návod na použití každé metody.

jak provést lineární regresi v Excelu pomocí analytického ToolPak

tento příklad ukazuje, jak spustit regresi v Excelu pomocí speciálního nástroje, který je součástí doplňku Analysis ToolPak.

povolit doplněk Analysis ToolPak

Analysis ToolPak je k dispozici ve všech verzích aplikace Excel 2019 až 2003, ale ve výchozím nastavení není povolen. Musíte jej tedy zapnout ručně. Zde je návod:

1. v aplikaci Excel klikněte na soubor > Možnosti.
2. v dialogovém okně Možnosti aplikace Excel vyberte Doplňky na levém postranním panelu, ujistěte se, že doplňky aplikace Excel jsou vybrány v okně Správa a klepněte na tlačítko Přejít.
   
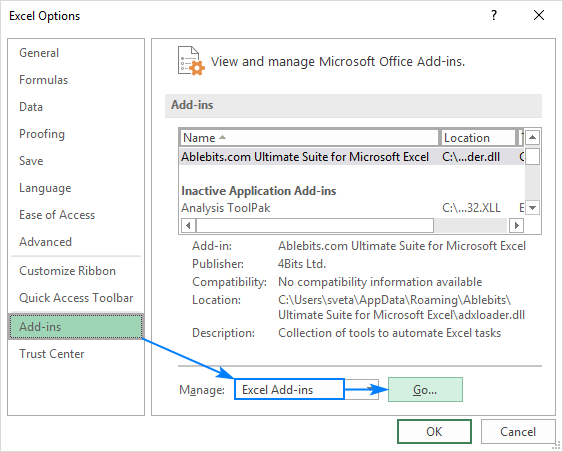
3. V doplňky dialogové okno, zaškrtněte políčko Analytické nástroje a klepněte na tlačítko OK:
   

Toto přidá nástrojů pro Analýzu Dat na kartě Data aplikace Excel stuhou.

spusťte regresní analýzu

v tomto příkladu provedeme jednoduchou lineární regresi v aplikaci Excel. To, co máme, je seznam průměrných měsíčních srážek za posledních 24 měsíců ve sloupci B, což je naše nezávisle proměnná (prediktor), a počet deštníky prodává ve sloupci C, což je závislá proměnná. Samozřejmě, existuje mnoho dalších faktorů, které mohou mít vliv na prodeje, ale pro teď jsme se zaměřit pouze na tyto dvě proměnné: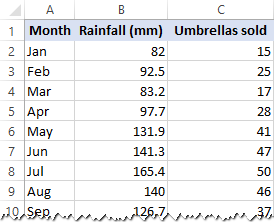

Analytické nástroje přidáno povoleno provádět tyto kroky k provedení regresní analýzy v Excelu:

1. Na kartě Data ve skupině Analýza, klepněte na Analýzu Dat tlačítko.
   
2. Vyberte regresi a klikněte na OK.
   
3. v dialogovém okně regrese nakonfigurujte následující nastavení:
   • Vyberte rozsah vstupu Y, což je závislá proměnná. V našem případě jde o prodej zastřešující (C1: C25).
   • Vyberte rozsah vstupního X, tj. vaši nezávislou proměnnou. V tomto příkladu se jedná o průměrné měsíční srážky (B1: B25).

   Pokud vytváříte vícenásobný regresní model, vyberte dva nebo více sousedních sloupců s různými nezávislými proměnnými.

   • zaškrtněte políčko Štítky, pokud jsou v horní části rozsahů X a Y záhlaví.
   • vyberte preferovanou možnost výstupu, v našem případě nový list.
   • volitelně zaškrtněte políčko Residuals, abyste zjistili rozdíl mezi předpokládanými a skutečnými hodnotami.
     
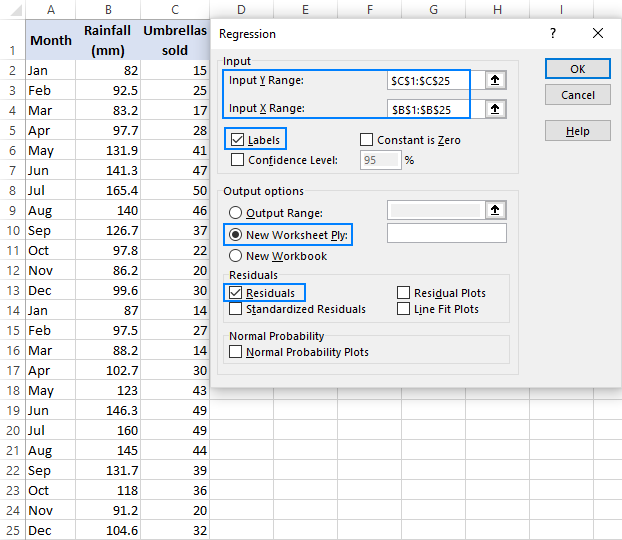
4. klikněte na OK a sledujte výstup regresní analýzy vytvořený aplikací Excel.

Interpretovat regresní analýzy výstup

Jak jste právě viděli, běh regrese v aplikaci Excel, je snadné, protože všechny výpočty jsou vytvarované automaticky. Interpretace výsledků je trochu složitější, protože potřebujete vědět, co je za každým číslem. Níže naleznete rozpis 4 hlavních částí výstupu regresní analýzy.

výstup regresní analýzy: souhrnný výstup

tato část vám řekne, jak dobře vypočítaná lineární regresní rovnice odpovídá vašim zdrojovým datům.

Tady je to, co každý kus informace znamená:

Více R je Korelační Koeficient, který měří sílu lineárního vztahu mezi dvěma proměnnými. Korelační koeficient může být libovolná hodnota mezi -1 a 1 a jeho absolutní hodnota označuje sílu vztahu. Čím větší je absolutní hodnota, tím silnější vztah:

• 1 znamená silný pozitivní vztah
• -1 znamená silný negativní vztah
• 0 znamená žádný vztah vůbec

R Square. Jedná se o koeficient určení, který se používá jako ukazatel dobré kondice. Ukazuje, kolik bodů spadá na regresní přímku. Hodnota R2 se vypočítá z celkového součtu čtverců, přesněji je to součet čtvercových odchylek původních dat od průměru.

v našem příkladu je R2 0,91 (zaokrouhleno na 2 číslice), což je víla dobrá. To znamená, že 91% našich hodnot odpovídá modelu regresní analýzy. Jinými slovy, 91% závislých proměnných (hodnoty y) je vysvětleno nezávislými proměnnými (hodnoty x). Obecně se R na druhou 95% nebo více považuje za vhodné.

upravený čtverec R. Jedná se o čtverec R upravený pro počet nezávislých proměnných v modelu. Tuto hodnotu budete chtít použít místo čtverce R pro vícenásobnou regresní analýzu.

standardní chyba. To je další goodness-of-fit opatření, které ukazuje na přesnost regresní analýzy – čím menší číslo, tím jistější si můžete být o regresní rovnici. Zatímco R2 představuje procento rozptylu závislé proměnné, která je vysvětlena pomocí modelu, Standardní Chyba je absolutní měřítko, které udává průměrnou vzdálenost, že datové body padají z regresní přímky.

pozorování. Je to prostě počet pozorování ve vašem modelu.

Regresní analýzy výstup: ANOVA

druhá část výstupu je Analýza Rozptylu (ANOVA):

v Podstatě, to se rozdělí na součet čtverců na jednotlivé komponenty, které poskytují informace o úrovni variability uvnitř vašeho regresní model:

• df je počet stupňů volnosti spojené s zdrojů rozptylu.
• SS je součet čtverců. Čím menší je zbytkový SS ve srovnání s celkovým SS, tím lépe se váš model hodí k datům.
• MS je střední čtverec.
• F je F statistika nebo F-test pro nulovou hypotézu. Používá se k testování celkového významu modelu.
• Význam F je P-hodnota F.

ANOVA část je zřídka používá pro jednoduchý lineární regresní analýzy v Excelu, ale rozhodně byste měli mít blíže podívat na poslední složkou. Hodnota význam F dává představu o tom, jak spolehlivé (statisticky významné) jsou vaše výsledky. Pokud je významnost F menší než 0,05 (5%), váš model je v pořádku. Pokud je větší než 0,05, pravděpodobně byste měli zvolit jinou nezávislou proměnnou.

Regresní analýzy výstup: koeficienty

Tato část poskytuje konkrétní informace o součásti své analýzy:

jeden z nejvíce užitečných komponent v této části je Koeficienty. To vám umožní vytvářet lineární regresní rovnice v aplikaci Excel:

Pro náš soubor dat, kde y je počet deštníky prodává a x je průměrné měsíční srážky, naše lineární regrese vzorec je následující:

Y = Rainfall Coefficient * x + Intercept

Vybaven s a b hodnoty jsou zaokrouhleny na tři desetinná místa, to se změní na:

Y=0.45*x-19.074

například, s průměrné měsíční srážky se rovná 82 mm, deštník prodeje by být přibližně 17.8:

0.45*82-19.074=17.8

V stejným způsobem, můžete zjistit, kolik deštníky se bude prodávat s jiným měsíční srážky (x proměnná) zadáte.

Regresní analýzy výstup: rezidua

v Případě porovnání předpokládané a skutečné číslo prodaných slunečníky odpovídající měsíční srážky 82 mm, uvidíte, že tato čísla jsou mírně odlišné:

• Odhadovaný: 17.8 (vypočteno výše)
• skutečné: 15 (řádek 2 zdrojových dat)

proč je rozdíl? Protože nezávislé proměnné nejsou nikdy dokonalými prediktory závislých proměnných. A reziduí může pomoci pochopit, jak daleko, skutečné hodnoty se od předpokládané hodnoty:

Jak si vyrobit lineární regrese grafu v aplikaci Excel

Pokud potřebujete rychle vizualizovat vztah mezi dvěma proměnnými, nakreslete lineární regrese grafu. To je velmi snadné! Zde je návod:

1. Vyberte dva sloupce s daty, včetně záhlaví.
2. Na Vložené kartě, v Chatech skupinu, klepněte na tlačítko Scatter chart icon, a vyberte Bodový miniatura (první):
   

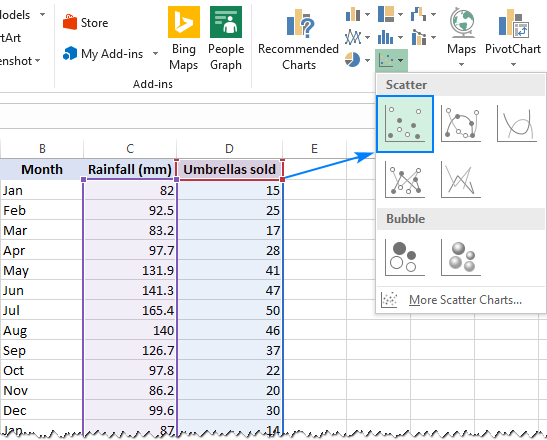
   Tento bude-li vložit bodový graf v listu, který se bude podobat tomuto:
   

3. potřebujeme k tomu nejmenších čtverců regresní přímky. Chcete-li to udělat, klikněte pravým tlačítkem na libovolný bod a v kontextové nabídce vyberte Přidat Trendline….
   
4. v pravém podokně, vyberte Lineární trendová linie tvaru a, volitelně, zaškrtněte Zobrazit Rovnici na Grafu, aby si vaše regresní vzorec:
   

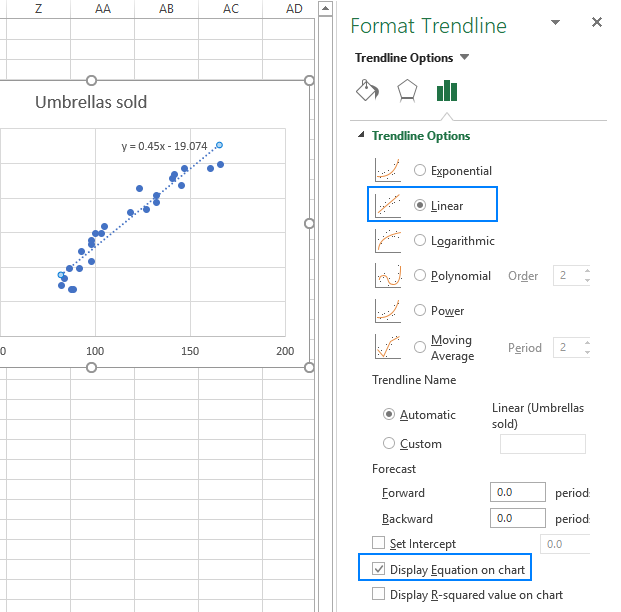
   Jak sis mohl všimnout, že regresní rovnice Excel vytvořila pro nás to je stejný jako lineární regrese vzorec, který jsme postavili na základě Koeficientů výstupu.

5. přepněte na výplň & řádek a přizpůsobte řádek podle svých představ. Například, můžete si vybrat jinou barvu čáry a používat pevnou linku místo přerušovaná čára (vyberte Pevné linky v Dash zadejte):
   

V tomto bodě, graf už vypadá jako slušný regresní graf:

Stále, možná budete chtít udělat pár vylepšení:

• Přetáhněte rovnice kdekoli uznáte za vhodné.
• přidat názvy os (tlačítko Elements grafu > názvy os).
• pokud vaše datové body začínají uprostřed vodorovné a / nebo svislé osy, jako v tomto příkladu, možná se budete chtít zbavit nadměrného prázdného místa. Následující tip vysvětluje, jak to provést: měřítko OS grafu zmenší bílé místo.

  A takto vypadá náš vylepšený regresní graf:
  

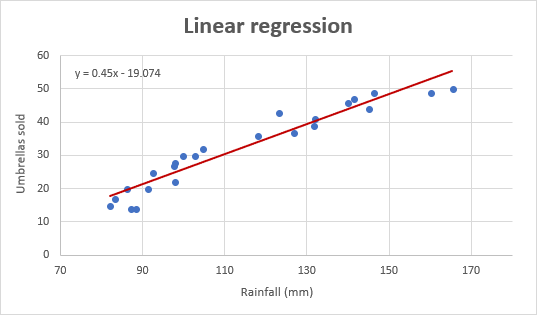  Důležitá poznámka! V regresním grafu by nezávislá proměnná měla být vždy na ose X a závislá proměnná na ose Y. Pokud je váš graf vykreslen v opačném pořadí, vyměňte sloupce v listu a nakreslete graf znovu. Pokud nemáte povoleno uspořádat zdrojová data, můžete přepínat osy X a Y přímo v grafu.

Jak na regresi v aplikaci Excel pomocí vzorců

aplikace Microsoft Excel má několik statistických funkcí, které vám mohou pomoci udělat lineární regresní analýzu, jako jsou funkce LINREGRESE, SKLON, INTERCPET, a funkce CORREL.

funkce LINEST používá regresní metodu nejmenších čtverců k výpočtu přímky, která nejlépe vysvětluje vztah mezi proměnnými a vrací pole popisující tuto přímku. Podrobné vysvětlení syntaxe funkce najdete v tomto tutoriálu. Pro teď, pojďme udělat vzorce pro náš ukázkový datový soubor:

=LINEST(C2:C25, B2:B25)

Protože tato funkce vrací matici hodnot, musí být zadán jako maticový vzorec. Vyberte dvě sousední buňky ve stejném řádku, E2:F2 v našem případě zadejte vzorec a dokončete jej stisknutím kláves Ctrl + Shift + Enter.

vrátí vzorec b koeficient (E1) a konstantní (F1) pro již známé lineární regresní rovnice:

y = bx + a

Pokud se můžete vyhnout pomocí maticové vzorce v listech, můžete vypočítat a a b jednotlivě s pravidelné vzorce:

Získat Y-intercept (a):

=INTERCEPT(C2:C25, B2:B25)

Získat svahu (b):

=SLOPE(C2:C25, B2:B25)

kromě toho, můžete najít korelační koeficient (Násobek R v regresní analýze souhrnný výstup), která udává, jak silně tyto dvě proměnné jsou spojeny k sobě navzájem:

=CORREL(B2:B25,C2:C25)

následující screenshot ukazuje, všechny tyto aplikace Excel regrese vzorce v akci:

takto provádíte lineární regresi v aplikaci Excel. To znamená, že mějte na paměti, že Microsoft Excel není statistický program. Pokud potřebujete provést regresní analýzu na profesionální úrovni, možná budete chtít použít cílený software, jako je XLSTAT, RegressIt atd.

dostupné stahování:

Chcete-li se blíže podívat na naše lineární regresní vzorce a další techniky popsané v tomto tutoriálu, můžete si stáhnout ukázkovou regresní analýzu v sešitu aplikace Excel.

• Jak používat Řešitele v Excelu s příklady
• Jak vypočítat složeného úroku v aplikaci Excel
• Jak vypočítat CAGR (compound annual growth rate) v aplikaci Excel