Komplexní Čísla: Úvod (strana 1 ze 3),

Oddílů: Úvod, Operace s komplexy, Kvadratický Vzorec,

až do teď, jste řekl, že nemůžete vzít druhou odmocninu ze záporného čísla. To proto, že jsem žádná čísla, které byly negativní po vás bych druhou (takže nemůžete „jít zpět“ tím, že odmocnina). Každé číslo bylo kladné poté, co jste ho na druhou. Takže jste nemohli moc dobře odmocnit negativní a očekávat, že přijdete s něčím rozumným.

nyní však můžete vzít druhou odmocninu záporného čísla, ale zahrnuje to použití nového čísla. Toto nové číslo bylo vynalezeno(objeveno?) v době reformace. V té době nikdo nevěřil, že jakýkoliv „skutečný svět“ využití by se našlo pro tuto novou řadu, jiné než uvolnění výpočty podílející se na řešení některých rovnic, takže nové číslo byl viděn jako předstírat, že počet vynalezl pro pohodlí zájmu.

(ale když se nad tím zamyslíte, nejsou všechna čísla vynálezy? Není to tak, že by čísla rostla na stromech! Žijí v našich hlavách. Všechny jsme si je vymysleli! Proč nevymýšlet nový, pokud to funguje v pořádku s tím, co již máme?)

:

Nyní, můžete si myslet, můžete to udělat:

Ale tohle nedává žádný smysl! Už máte dvě čísla, která čtverec na 1; jmenovitě -1 a + 1. A už jsem čtverečky na -1. Takže není rozumné, že bych také čtverec na 1. To poukazuje na důležitý detail: Při jednání s představy, získat něco (schopnost vypořádat se s negativy uvnitř odmocniny), ale také ztratit něco (některé z pružnosti a pohodlné pravidel, které jste zvyklí mít při jednání s odmocniny). Zejména musíte vždy udělat první část i!

• Zjednodušte sqrt (-9). Copyright © Elizabeth Stapel 2000-2011 Všechna Práva Vyhrazena

(Pozor: krok, který jde přes třetí „rovná se“ přihlásit se “ “ ne „„. I je mimo radikál.)

• Zjednodušte sqrt(-25).

• Zjednodušte sqrt(-18).

• Zjednodušte-sqrt(-6).

Ve své výpočty, budete řešit já, stejně jako byste s x, s výjimkou skutečnosti, že x2 je jen x2, ale i2 je -1.

• Zjednodušit 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Zjednodušit 16i – 5i.

16i – 5i = (16-5) i = 11i

• vynásobte a zjednodušte (3i) (4i).

(3i)(4i) = (3·4) (·i) = (12)(i2) = (12)(-1) = -12

• Násobit a zjednodušit (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

Poznámka: tento poslední problém. V něm můžete vidět, že , protože i2 = -1. Pokračování, dostaneme:

Tento vzor pravomocí, znamení, 1, a já je cyklus:

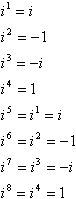
jinými slovy, pro výpočet jakékoli vysoký výkon i můžete ji převést na nižší výkon tím, že nejbližší násobek 4, který není větší než exponent a odečtením této více z exponentu. Například, společný chyták v testech je něco podél linek „Zjednodušit i99“, myšlenka je, že budete to zkusit vynásobit jsem devadesát devět krát a budete dojdou času, a učitelé budou mít dobrý smích na vaše náklady ve sborovně. Zde je, jak zkratka funguje:

i99 = i96+3 = i(4×24)+3 = i3 = –i,

To znamená, i99 = i3, protože můžete jen lop z i96. (Devadesát šest je násobek čtyř, takže i96 je jen 1, což můžete ignorovat.) Jinými slovy, můžete rozdělit exponent o 4 (pomocí dlouhého dělení), zahodit odpověď a použít pouze zbytek. To vám dá část exponentu, na které vám záleží. Zde je několik dalších příkladů:

• Zjednodušte i17.

i17 = i16 + 1 = i4 * 4 + 1 = i1 = i

• Zjednodušte i120.

i120 = i4 * 30 = i4 * 30 + 0 = i0= 1

• Zjednodušte i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>