Fibonacciho Posloupnost
Fibonacciho Posloupnost je řada čísel:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
další číslo je nalezena sečtením dvou čísel před ním:
- 2 je zjištěno, že přidáním dvou čísel před ním (1+1),
- 3 je zjištěno, že přidáním dvou čísel před ním (1+2),
- 5 (2+3),
- a tak dále!
příklad: další číslo ve výše uvedeném pořadí je 21+34 = 55
je to tak jednoduché!
zde je delší seznam:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
můžete zjistit několik dalších čísel?
Dělá Spirály
Když jsme se, aby čtverce s těmito šířky, dostaneme pěknou spirálu:
vidíte, jak čtverce vejde dohromady?
například 5 a 8 dělají 13, 8 a 13 dělají 21 a tak dále.

tato spirála se nachází v přírodě!
Viz: Fibonacci
pravidlo
Fibonacciho posloupnost může být zapsána jako „pravidlo“ (viz sekvence a řady).
nejprve jsou termíny číslovány od 0 takto:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
termín číslo 6 se nazývá x6 (což se rovná 8).
|
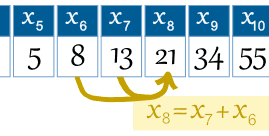
Příklad: 8 termín je x8 = x7 + x6 |
 |
Takže můžeme napsat, že pravidlo:
Pravidlo je xn = xn−1 + xn−2
kde:
- xn je termín číslo „n“
- xn−1 je předchozí člen (n−1)
- xn−2 je výraz, než že (n−2)
Příklad: termín 9 se vypočte takto:
Zlatý Poměr
A tady je překvapení. Když vezmeme dvě po sobě jdoucí (jedna po druhé) Fibonacciho čísla, jejich poměr je velmi blízký zlatému poměru „φ“, který je přibližně 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
nemusíme začít s 2 a 3, tady jsem náhodně vybral 192 a 16 (a dostal sekvence 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
získání dobrých hodnot trvá déle, ale ukazuje, že to dokáže nejen Fibonacciho sekvence!
Použití Zlatý Poměr pro Výpočet Fibonacciho Čísel.
A ještě více překvapující je, že můžeme vypočítat Fibonacciho Číslo pomocí Golden Ratio:
xn = φn − (1−φ)n√5
odpověď vyjde jako celé číslo, přesně rovna kromě předchozích dvou podmínek.
příklad: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
Když jsem na to použil kalkulačku (pouze zadáním zlatého poměru na 6 desetinných míst), dostal jsem odpověď 8.00000033, přesnější výpočet by byl blíže k 8.
zkuste n = 12 a uvidíte, co dostanete.
můžete Si také vypočítat Fibonacciho Čísla vynásobením předchozí Fibonacciho Číslo, Zlatý řez a pak zaokrouhlování (funguje pro čísla větší než 1):
Příklad: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (zaoblené)
některé zajímavé věci
zde je Fibonacciho posloupnost znovu:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Tam je zajímavý vzor,
- Podívejte se na číslo, x3 = 2. Každé 3. číslo je násobkem 2 (2, 8, 34, 144, 610, …)
- Podívejte se na číslo x4 = 3. Každé 4. číslo je násobkem 3 (3, 21, 144, …)
- Podívejte se na číslo x5 = 5. Každé 5. číslo je násobkem 5 (5, 55, 610, …)
a tak dále (každé n-tý číslo je násobkem xn).
1/89 = 0.011235955056179775…
Všimněte si, že prvních několik číslic (0,1,1,2,3,5) je Fibonacciho posloupnost?
V, jak jsou všichni, kromě několika čísel (13, 21, atd.) se překrývají, jako je tento:
… atd …
0.011235955056179775… = 1/89
Podmínky Pod Nulou
pořadí prací pod nulou také, jako je tento:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Dokázat, že každé číslo je nalezena sečtením dvou čísel před ním!)
ve skutečnosti má sekvence pod nulou stejná čísla jako sekvence nad nulou, kromě toho, že následují a+ -+ – … vzor. To lze zapsat takto:
x−n = (-1)n+1 xn
, Který říká, že termín „−n“ se rovná (-1)n+1 krát období „n“, a hodnotu (-1)n+1 úhledně dělá správnou +1, -1, +1, -1, … vzor.
historie
Fibonacci nebyl první, kdo věděl o sekvenci, to bylo známé v Indii stovky let předtím!

O Fibonacciho Muž
Jeho pravé jméno je Leonardo Pisano Bogollo, a on žil v letech 1170 až 1250 v Itálii.
„Fibonacci“ byla jeho přezdívka, což zhruba znamená „Syn Bonacciho“.
stejně Jako je známý pro Fibonacciho Posloupnost, pomohl šířit Hind-arabské Číslice (jako naše současná čísla 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) přes Evropu v místě Římské Číslice (I, II, III, IV, V, atd.). To nám všem ušetřilo spoustu problémů! Děkuji Leonardo.

Fibonacciho Den
Fibonacciho Den je 23. listopadu, jak to má číslice „1, 1, 2, 3“, který je součástí sekvence. Takže příští listopad 23 dejte všem vědět!


Leave a Reply