S kasovní úspěch filmu „Interstellar“, mnoho lidí jsou nadšeni vyhlídky červí díry jako prostředek pro mezihvězdné dopravy. I když v současné době neexistuje žádný důkaz, že tyto exotické objekty existují v přírodě, je možné, že by mohl být uměle vytvořen, snad od verze vyšší dimenzionální teorie strun a inženýrství základní časoprostorové pěny. Výzkum červích děr je dnes vzrušující téma s desítkami článků publikovaných v recenzovaných časopisech každý rok, ale stojí za to připomenout jeho původ — a to začíná od překvapivé místo.

v roce 1915 Albert Einstein publikoval svou obecnou teorii relativity, popis gravitace, který úhledně definuje, jak se objekty navzájem přitahují a ovlivňují prostor a čas kolem nich. O mnoho let později americký fyzik John Wheeler minul frázi „vesmír říká hmotě, jak se pohybovat, a hmota říká vesmíru, jak se zakřivit“. Einstein popsal gravitaci jako projev časoprostorového zakřivení. Obecná relativita je spojitá teorie pole na rozdíl od teorie částic hmoty, která vedla ke kvantové mechanice.

Einstein se také podílel na vývoji kvantové mechaniky, teorie, která popisuje subatomární částice. Nebyl však zcela spokojen s jeho vlastní nejistotou a pravděpodobnostním charakterem. Takže v roce 1935 pracoval s Nathanem Rosenem na vytvoření teorie pole pro elektrony pomocí obecné relativity. Jejich práce byla nazvána „problém částic v obecné teorii Relativity“. Einstein a Rosen byli vyšetřování možnosti rozdrobená teorie hmoty a elektrické energie, který, kromě nespojitosti (singularity) v poli, z použít žádné jiné proměnné jiného, než popis (metrické) obecné relativity a Maxwellovy elektromagnetické teorie. Jedním z důsledků bylo, že bylo zjištěno, že nejzákladnější nabitá částice má nulovou hmotnost.

nakonec to, co vyrobili, bylo něco zcela originálního. Začali s rovnice pro sféricky symetrické rozložení hmotnosti, již používá pro černé díry, a je známo jako Schwarzschildův řešení,

$$ds^2 = -\dfrac{1}{1-2m/r}dr^2 – r^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)dt^2$$

, kde \(ds^2\) je metrický a \(m=GM/c^2\) s sférické souřadnice \((r,\theta,\phi)\) a \(t\).

provedena transformace souřadnic odstranit oblasti obsahující zakřivení singularity, diskontinuitu v prostoru zakřivení předpokládané černé díry a podobné jevy. Singularity na \(r=2m\) byla odstraněna transformace souřadnic \(u^2 = r – 2m\), což v konečném řešení,

$$ds^2 = -4(u^2 + 2m)du^2 – (u^2 + 2m)^2 d\Omega^2 + \dfrac{u^2}{u^2 + 2m} dt^2$$

, kde \(d\Omega^2 = d\theta^2 + \sin^2\theta d\phi^2\).

toto řešení bylo matematické znázornění fyzického prostoru prostorem dvou asymptoticky plochých listů Spojených mostem nebo Schwarzschildovou červí dírou s „hrdlem“. To spojuje dva listy a analogicky dvě oddělené části skutečného, trojrozměrného vesmíru. Obrázek 1 ukazuje prostor kolem červí díry, přičemž prostor nad a pod se při oddálení do nekonečna stává plochým na „okrajích“.

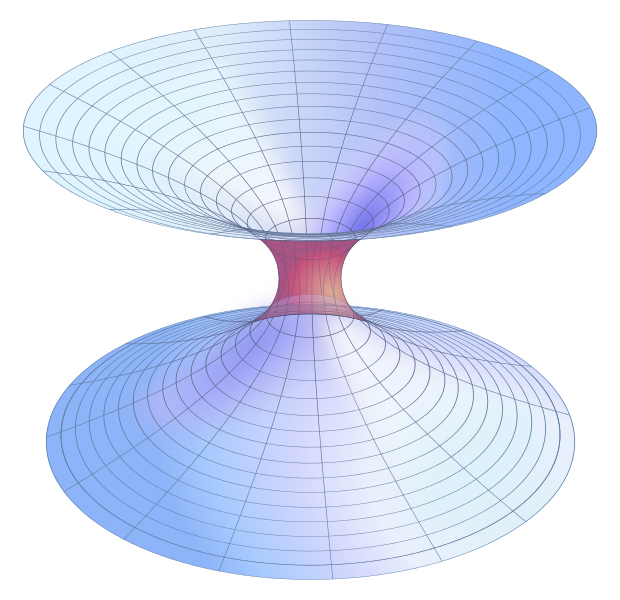
Teď to není červí díry, pro které jsme museli vyčkat na příjezd fyzikové John Wheeler v roce 1950 a Kip Thorne v roce 1980. V roce 1987, s podporou Carl Sagan pro jeho román „Kontakt“ (později celovečerní film), Thorne a jeho kolega Michael Morris byli schopni vytvořit matematický popis, metrické, popsat sféricky symetrické a statické červí dírou s real, konečný, obvod. To mělo souřadnici snižující se od záporného nekonečna-v minimálně zakřiveném prostoru-na minimální hodnotu, kde bylo umístěno hrdlo, a poté se zvyšující od hrdla k pozitivnímu nekonečnu-v jiném minimálně zakřiveném prostoru. Toto řešení má charakteristickou vlastnost, že nemá žádný horizont událostí-na rozdíl od černé díry. Kniha Thorne a Morris byla nazvána „červí díry v časoprostoru a jejich použití pro mezihvězdné cestování: Nástroj pro výuku obecné Relativity“. Tento článek pomohl založit výzkum červích děr jako novou oblast akademického šetření.

Od té doby, mnoho dokumentů byla zveřejněna, a skutečně astronomické průzkumy byly provedeny, zkoumá nejvzdálenější hvězdy a galaxie při hledání přirozené červí díry. Žádný nebyl identifikován, ale pamatujte, původ této oblasti výzkumu — Einstein-Rosenův Most nebyl červí díry, a to ani nebyl autorův záměr vyrábět, ale oni vytvořili první matematický popis červí díru. Měli by si je pamatovat. Vědecký výzkum často produkuje něco zcela neočekávaného s důsledky, které sahají daleko za původní záměry vědců.

Kelvin F. Dlouho

co tento článek byl publikován, náš časopis, Principium, vydal dvě otázky (otázky 9 & 10), kde jsme diskutovali o červích dírách a Einstein-Rosenův Most podrobněji. Tyto otázky také podrobně jeden den sympozia na „Mezihvězdné červí Díry: Fyzika a Praktické Realizaci“ pořádá Iniciativa pro Mezihvězdné Studií ve spolupráci s British Interplanetary Society.