Definitivní integrály
možná si nejprve přečtete Úvod do integrace!
Integrace
|
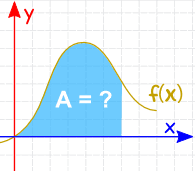
Integrace může být použit k nalezení plochy, objemy, centrál bodů a mnoho užitečných věcí. Ale to je často používáno k najít oblast pod grafem funkce, jako je tento: |
 |
|
|
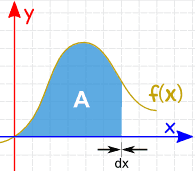
oblast lze nalézt přidáním plátky, které blížit k nule, v šířka: A tam jsou Pravidla Integrace, které nám pomohou dostat odpověď. |
 |
Zápis
symbol „Integral“ je stylové „S“ (pro „Součet“, myšlenka sčítání plátky):
Poté, co Nedílnou Symbol klademe funkce chceme najít integrál (nazývá Integrand).
a pak dokončete DX, což znamená, že řezy jdou ve směru x (a blíží se k nule na šířku).
určitý integrál
určitý integrál má počáteční a koncové hodnoty: jinými slovy existuje interval .
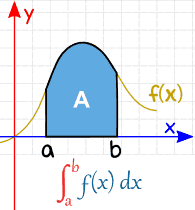
a A b (nazývané limity, hranice nebo hranice) jsou umístěny v dolní a horní části „S“, takto:
 |
 |
|
| Definite Integral (from a to b) |
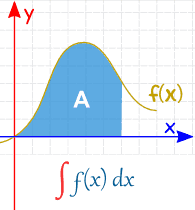
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
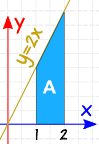
Příklad: kolik je 2 ∫ 1 2x dx
Jsme žádáni pro Určitý Integrál od 1 do 2 2x dx.
Nejprve musíme najít Neurčitý Integrál.
Pomocí Pravidla Integrace zjistíme, že ∫2x dx = x2 + C,
Nyní spočítat, že na 1 a 2:
- x=1: ∫2x dx = 12 + C
- x=2: ∫2x dx = 22 + C
Odečíst:
a „C „se zruší… takže s Integrálů můžeme ignorovat. C.
Výsledek:

Zkontrolujte, zda: s takový jednoduchý tvar, pojďme také zkusit výpočtu oblasti geometrie:
= 2+42 × 1 = 3
Ano, to má oblast 3.
(Hurá!)
notace: Můžeme ukázat neurčitý integrál (bez +C) uvnitř hranatých závorek, s limity a a b po, jako je tento:
Příklad (pokračování)
dobrý způsob, jak ukázat vaši odpověď:
=
zkusme další příklad:
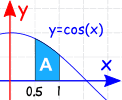
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
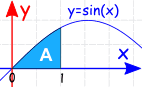
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
Neurčitý Integrál: ∫sin(x) dx = −cos(x) + C
Když jdeme z 0, můžeme vypočítat integrál v x=1?
−p> – cos (1) = -0.540…
Co? Je to negativní? Ale v grafu to vypadá pozitivně.
dobře … udělali jsme chybu!
protože musíme odečíst integrál na x=0. Neměli bychom předpokládat, že je nula.
udělejme to tedy správně, odečteme jedno od druhého:
=
to je lepší!
Ale můžeme mít negativní regionů, kdy křivka je pod osou:
Příklad:
Určitý Integrál od 1 do 3, cos(x) dx:
Všimněte si, že některé jsou pozitivní a některé negativní.
určitý integrál bude pracovat na čisté hodnotě.
Udělejme výpočty:
=
skok je více negativní než pozitivní s čistým výsledkem -0,700….
takže si musíme pamatovat tuto důležitou věc:
Zkuste integrace cos(x) s různou počáteční a koncové hodnoty vidět pro sebe, jak klady a zápory práce.
Pozitivní Oblasti
Ale někdy chceme, aby všechny ošetřené plochy jako pozitivní (bez části pod osou je odečtena).
V tom případě musíme vypočítat oblastech odděleně, jako v tomto příkladu:

Příklad: Jaká je celková plocha mezi y = cos (x) a osou x, od x = 1 do x = 3?
je to jako příklad, který jsme právě udělali, ale nyní očekáváme, že celá oblast je pozitivní (představte si, že jsme ji museli malovat).
Takže teď musíme udělat, díly samostatně:
- pro oblasti nad osou x
- Jeden pro oblast pod osou x
křivka protíná osu x v bodě x = π/2 takže máme:
Od 1 do π/2:
= sin(π/2) − sin(1)
Z π/2 na 3:
= sin(3) − sin(π/2)
poslední jeden vyjde negativní, ale chceme, aby to bylo pozitivní, takže:
Celková plocha = 0.159… + 0.859… = 1.018…
To se velmi liší od odpovědi v předchozím příkladu.
Kontinuální
ano, funkce jsme integraci musí být Souvislý mezi a a b: ne otvory, skoky nebo vertikální asymptoty (kde funkce hlavy nahoru/dolů směrem k nekonečnu).
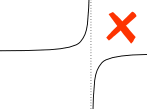
Příklad:
vertikální asymptotu mezi a a b ovlivňuje určitý integrál.
Vlastnosti
Oblast nad − oblast pod
nedílnou přidá oblasti nad osou, ale odečte plocha, níže, pro „čistou hodnotu“:
Přidání Funkce
integrál z f+g se rovná integrál z f plus integrál g:
Couvací interval
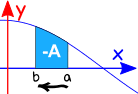
Obrácení směru interval dává negativní původního směru.
![]()


Leave a Reply