beanz Časopis
Mapa o Merian-Erben (1652) na Wikipedii
Tento měsíc je matematika puzzle se datuje k roku 1735, kdy byl poprvé vyřešil Leonhard Euler, Švýcarský matematik a fyzik.
hádanka se nazývá sedm mostů Königsbergu. Je založen na skutečném městě, pak v Prusku, nyní Kaliningrad v Rusku. Město je rozděleno řekou se dvěma ostrovy mezi nimi a, dále po proudu, řeka znovu rozděluje město.
problém je zdánlivě jednoduchý: existuje (nebo bylo v Eulerově době) sedm mostů, které spojují dva ostrovy a navazující části města. Euler přemýšlel, jestli by člověk mohl projít každý ze sedmi mostů jednou a jen jednou, aby se dotkl každé části města. Start a konec na stejném místě nebyl podmínkou.
Tady je mapa, můžete použít, aby se pokusila vyřešit tento problém pro sebe:
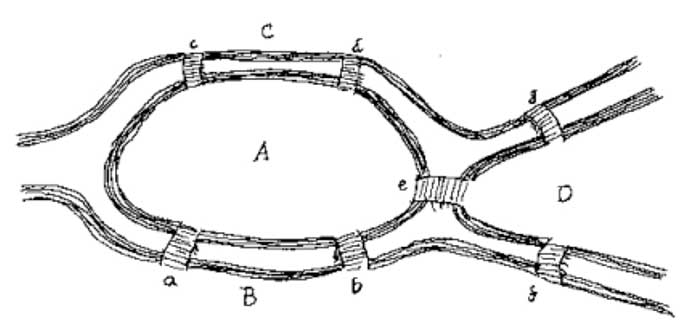
, Které si myslíte, že je důležitější, aby tento problém vyřešit: počet mostů nebo umístění každého mostu?
odpověď: počet mostů.
Euler dokázal, počet mostů musí být sudé číslo, například, šest mostů namísto sedmi, pokud chcete projít přes každý most jednou a cestování do každé části Königsberg. Řešení vidí každý Most jako koncový bod, vrchol z matematického hlediska a spojení mezi každým mostem (vrcholem). Euler si uvědomil, že pouze sudý počet mostů přinesl správný výsledek toho, že se mohl dotknout každé části města, aniž by dvakrát překročil most.
Euler použil matematiku, aby dokázal, že není možné překročit všech sedm mostů pouze jednou a navštívit každou část Königsbergu. Tím uvedl do pohybu řadu objevů a poznatků o tom, jak lze definovat prostor a protínající se prostory, jakož i jejich vlastnosti. Podrobný popis Eulerova řešení v odkazu na Wikipedii pod tímto článkem.
Pokud jste někdy viděli například pás mobius, viděli jste příklad topologie, matematický obor se vyvinul z Eulerova řešení tohoto problému. Topologie se zabývá prostorem a tím, jak se věci navzájem propojují, stejně jako kontinuita a hranice prostoru. Topologie také studuje, jak se vlastnosti prostoru mění a nemění se, když je prostor rozšířen nebo zkrácen.
ve výpočetní technice je topologie užitečná pro pochopení sítí (cest), které mohou proudit v jakémkoli systému, a také pro to, jak se soubory dat mohou navzájem vztahovat. Sedm Mostů města Královce je také podobné na další společné výpočetní problém zvaný někdy Problém obchodního Cestujícího, kde se pokusíte najít nejefektivnější trasu vzhledem k tomu, sadu omezení, jako je sedm mostů v Euler je problém.
nematematici (pravděpodobně vy, určitě já) zažívají problém s cestujícím prodavačem kdykoli nastoupíme do vlaku nebo autobusu. Problém cestující prodavač je přijít na nejefektivnější způsob, jak cestovat mezi dvojicemi měst stanovených vzdáleností. Správu omezených zdrojů (vlaky, autobusy), které cestují po konečnou trasy je to ideální řešení pro výpočetní řešit, protože počítače jsou rychlejší a efektivnější. Nejprve však potřebujeme Eulera a další, aby uvedli problém a definovali řešení pomocí matematiky. Pak jsme naprogramovat naše počítače dělat matematiku.
topologie se také zabývá teorií množin, jak lze skupiny věcí třídit do množin pro identifikaci společných prvků s jinými skupinami i jedinečných prvků. Vennův diagram je skvělým příkladem sady. A programování někdy musí třídit data různými způsoby. Která metoda třídění funguje nejlépe pro situaci, lze určit teorií množin.
a co se stalo se sedmi mosty z Eulerovy doby? Dva nepřežily druhou světovou válku. dva mosty byly zbořeny a nahrazeny jedinou dálnicí. Ze tří zbývajících mostů byl jeden přestavěn v roce 1935, zatímco další dva zůstávají nedotčeny, jak je Euler znal. A samozřejmě, Königsberg, Prusko změnilo svůj název na Kaliningrad, Rusko.
Leave a Reply