graf lineární nerovnosti v jedné proměnné je číselná čára. Použijte otevřený kruh pro < a > a uzavřený kruh pro ≤ a ≥.

graf pro x > -3

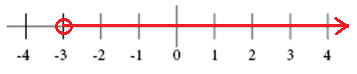
graf pro x ≥ 2

Nerovností, které mají stejné řešení, se nazývají ekvivalentní. Existují vlastnosti nerovností, stejně jako vlastnosti rovnosti. Všechny níže uvedené vlastnosti platí také pro nerovnosti zahrnující ≥ a ≤.

kromě majetku nerovnost říká, že přidání stejného množství do každé straně nerovnosti vytváří ekvivalentní nerovnosti

$$Pokud \: x>y,\: pak\: x+z>y+z$$

$$Pokud\: x<y,\: pak\: x+z<y+z$$

odčítání majetku nerovnost nám říká, že se odečte stejný počet z obou stran nerovnosti dává ekvivalentní nerovnosti.

$$Pokud \: x>y,\: pak\: x-az>y-z$$

$$Pokud\: x<y,\: pak\: x-z<y-z$$

znásobení majetku nerovnost nám říká, že násobení obou stran nerovnice kladným číslem produkuje ekvivalentní nerovnosti.

$ $ If \: x> y \: a\: z>0,\: pak\: xz>yz$$

$$Pokud\: x<y\: a\: z>0,\: pak\: xz<yz$$

Násobení v každé straně nerovnice záporné číslo na druhou stranu nepřináší ekvivalentní nerovnost, pokud bychom se také obrátit směr nerovnosti symbol

$$Pokud \: x>y \: a\: z<0,\: pak\: xz<yz$$

$$Pokud\: x<y\: a\: z<0,\: pak\: xz>yz$$

totéž platí i pro rozdělení majetku nerovnosti.

rozdělení obou stran nerovnosti s kladným číslem vytváří ekvivalentní nerovnost.

$$Pokud \: x>y \: a\: z>0,\: pak\: \frac{x}{z}>\frac{y}{z}$$

$$Pokud\: x<y\: a\: z>0,\: pak\: \frac{x}{z}<\frac{y}{z}$$

A dělení na obě strany nerovnice záporné číslo produkuje ekvivalentní nerovnost, pokud nerovnost symbol je obrácené.

$$Pokud \: x>y \: a\: z<0,\: pak\: \frac{x}{z}<\frac{y}{z}$$

$$Pokud\: x<y\: a\: z<0,\: pak\: \frac{x}{z}>\frac{y}{z}$$

Chcete-li vyřešit multi-krok nerovnost děláte, jak jste při řešení multi-step rovnice. Vezměte jednu věc v té době, nejlépe počínaje izolací proměnné od konstant. Při řešení vícestupňových nerovností je důležité nezapomenout zvrátit znaménko nerovnosti při násobení nebo dělení zápornými čísly.

Příklad:

Vyřešit nerovnost,

$$-2\left ( x+3 \right )<10$$