Jason McCormick
docent, Občanské & Environmentální Inženýrství, University of Michigan, Ann Arbor, MI, spojené státy

Chvíli připojení vyrobeny z obdélníkové a čtvercové duté konstrukční profily (HSS) obdržel menší pozornost ve srovnání s HSS–HSS připojení tvořen osově zatížené členy (T-, Y-, cross-a K-připojení). Většina statických studií zaměřených na tato připojení považovala systémy vazníků Vierendeel. Tyto systémy jsou často tvořeny čtvercový nebo obdélníkový horní a dolní akordy, které jsou spojeny s čtvercový nebo obdélníkový vertikální internetu (pobočka) členové (Obrázek 1). Jako výsledek této konfigurace, akord-na-web spojení prochází významnými ohýbání spolu s smyku a axiální zatížení a není považován za připnul připojení, jak se běžně provádí v typické truss systémy. Původně koncipován v roce 1896 Arthur Vierendeel, to nebylo až HSS byly vyvinuty, že potenciál pro Vierendeel vazníky začal být realizován (Korol et al. 1977), ale jejich použití vyžadovalo pochopení toho, jak přenášet moment mezi HSS-to-HSS T-spojení.

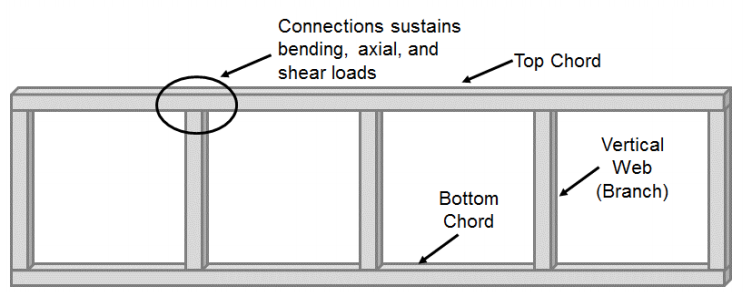
Mnoho z časných studií z těchto spojení se zaměřil na možnost spojení plně rozvinout chvíli kapacita pobočka členem. Jubb a Redwood (1966) ukázali, že když měl úsek větve stejnou šířku jako úsek akordu (β=1), bylo možné dosáhnout plné momentové kapacity člena HSS bez vyztužení. Tato studie však nezohlednila potenciální ztrátu momentové kapacity v důsledku přítomnosti axiálního zatížení. Na druhé straně Korol et al. (1977) ukázal, že spojení s menší pobočky šířka než akord nemohl vyvinout plnou chvíli kapacita pobočky, aniž by posílení prostřednictvím řady 29 různé testy připojení zvažuje, 5 různých konfigurací (nevyztužené, pobočka příruby výztužné desky, akord příruby, výztuhy, náběhy, a komolého jehlanu). Obecně se pevnost a tuhost nevyztužených spojení typu Vierendeel snižuje se zvýšením poměru štíhlosti akordu (B / t) a snížením poměru šířky větve k akordu (β). Jako výsledek, nevytuženém Vierendeel krovu typ spojení může být považována za rigidní (tj. podstoupit minimální relativní rotace mezi akord a pobočky), kdy pobočka-akord je poměr šířky 1.0 a akord štíhlostní poměr je nízká nebo je spojení zesílené (Packer 1993).

Protože maximální momenty v těchto kloubech se může objevit při příliš velké deformace, podobný přístup se používá pro osově zatížené čtvercové a obdélníkové HSS kloubů je přijala, kde o maximální nosnosti nebo deformace nebo rotace limit se používá k charakterizaci design moment (Wardenier 1982). AISC 360-10 (Kapitola K3) se domnívá, tři mezní stavy pro čtvercové a obdélníkové HSS T-spoje podle statické v-rovina ohybu: akord zdi plastifikační, bočnice místní výtěžkem, a místní výtěžkem pobočky vzhledem k nerovnoměrnému rozložení zatížení. Akord zdi plastifikační dochází v důsledku šířka větev člen je menší než šířka akord (β ≤ 0.85), které vyžadují napětí a komprese zatížení produkován ohybový moment, které mají být převedeny přes relativně flexibilní tvář akord, spíše než přímo na tužší bočnice. Mezní stav rovnice (AISC 360-10 Rovnice K3-6), mohou být odvozeny z výnosové linie teorie (viz Obrázek 2):

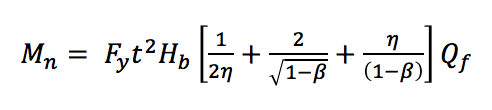
Mn je nominální moment kapacita připojení, Fy je uvedeno minimální mez kluzu akord, Hb je celková výška větev, h je zatížení, parametr délka se rovná výšce pobočky rozděleny podle šířky akord (za předpokladu, že 90o úhel mezi akord a pobočky členských jak je typické pro Vierendeel vazníky)a Qf je parametr snížit kapacitu kloubu v přítomnosti axiální komprese v akordu.

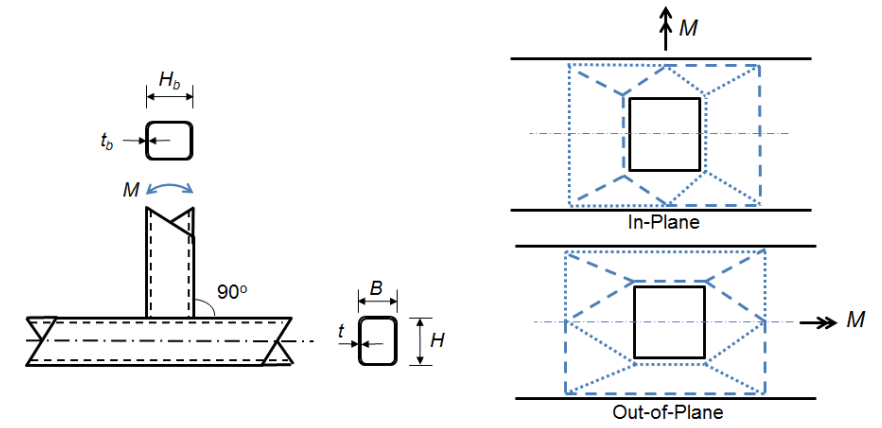
další dva mezní stavy jsou spojeny s připojení, kde šířka pobočka člena se rovná nebo téměř rovná šířce akord (β > 0.85) což znamená, že napětí a komprese zatížení vyvinut v přírubách pobočky členský jsou převedeny téměř přímo do tužší bočnice akordu. Mezní stav pro bočnice místní výtěžkem (AISC 360-10 Rovnice K3-7) T-spojení pak může být odvozena z webu místní výtěžkem rovnice pro koncentrované síly působící na vzdálenosti od konce členských větší než jeho hloubka (AISC 360-10 Rovnice J10-2):

Mn = 0.5Fyt(Hb + 5t)2
Rovnice 2,

Pro místní výtěžkem pobočky vzhledem k nerovnoměrnému rozložení zatížení (AISC 360-10 Rovnice K3-8) v T-spojení, efektivní šířka přístup se používá ke snížení kapacity osvěžující členské získat nominální moment používaná ortéza:

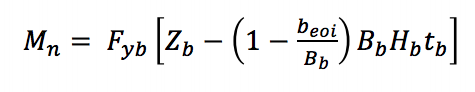
Fyb je uvedeno minimální mez kluzu pobočky, Zb je plastický průřezový modul pobočky v ose ohybu, beoi je efektivní šířka větev, Bb je celková šířka větev, a tb je design tloušťka stěny pobočky.

Protože tam je omezený experimentální důkazy na podporu konkrétních design, modely pro Vierendeel krovu připojení (T-spoje) v rámci out-of-plane ohýbání, podobně jako mezní stavy jako ty, v rovině ohýbání se používají (Packer et al. 2010). Jeden další mezní stav poruchy zkreslení akordu se vyvíjí z točivého momentu aplikovaného na akord členem větve v důsledku okamžiku mimo rovinu. Tento točivý moment může vést k kosočtverečnému zkreslení akordu. Rovnice jmenovitého momentu pro ohýbání mimo rovinu lze nalézt v rovnicích AISC 360-10 K3-9, K3-10, K3-11 a K3-12. Rovnice pro ohýbání T-spojení v rovině i mimo rovinu jsou podobné těm, které byly přijaty na mezinárodní úrovni (Packer et al. 2010).

výše uvedené konstrukční rovnice byly odvozeny s ohledem na Vierendeelovy příhradové systémy při statickém zatížení. Nedávná studie (Fadden et al. 2015), podporovala tuto práci za chování čtvercové a obdélníkové HSS–HSS okamžik spojení v rámci velké cyklické zatížení, pro použití v tubě-na základě seismické chvíli rámových systémů (střední a speciální moment, rámy). Takový systém se snaží využít vynikajících axiálních, ohybových a torzních vlastností, vysokého poměru pevnosti k hmotnosti a architektonicky příjemné povahy čtvercového a obdélníkového HSS. Vysoká torzní odolnost může vést ke snížení bočního vyztužení paprsku, zatímco vysoký poměr pevnosti k hmotnosti má za následek nižší seismickou hmotnost. Nicméně, tyto spoje musí být schopen podstoupit stabilní plastové závěsné paprsku členské kde 80% plastové kapacity paprsek člen je udržována buď 0.2 rad. (MMF) nebo 0,4 rad. (SMF) mezipodlažního driftu (AISC 341-10). Vzhledem k tomu, že aktuální seismické design okamžik rámových systémů vyžaduje většina nepružné chování se vyskytují v paprsku člen, paprsek člen také musí dosáhnout svého plného plastu kapacita před prochází lokální zborcení. Fadden a McCormick (2014a) oba považovány za experimentální a finite element modelů pro stanovení omezující šířku-tloušťka a hloubka-tloušťka požadavky pro HSS v ohybu, protože uvedené v aktuální AISC Seismické Ustanovení (AISC 341-10) byly z velké části vyvinut na základě zkoušek cyklických osově zatížené HSS členů.

určit vhodné konfigurace a podrobně požadavky pro splnění této pevnost a tažnost poptávky, čtyř různých konfigurací připojení byly experimentálně testovány: dva přímo svařované nevyztužené připojení (bezkonkurenční a uzavřeno) a dva zesílené spojení (přes desku a vnější membránový talíř). Všechna připojení využívala sloupec HSS 10x10x5/8. Přímo svařované spoje využívaly předkvalifikované svary CJP, jak je uvedeno v AWS D1. 1 (2010). Pro bezkonkurenční spojení byl paprsek HSS 12x8x3/8 (β = 0.8) což naznačuje, že plastifikace plochy kolony může být problémem. Pro odpovídající spojení byl nosník HSS 12x10x3/8 (β = 1,0) umožňující přenos zatížení přímo do boční stěny. K načtení spojení byl použit protokol načítání AISC pro předkvalifikaci připojení seismických momentů (AISC 341-10). Chování spoje byl, jak se očekávalo, s bezkonkurenční spojení vykazuje deformace ve sloupci tvář, zatímco připojení bylo uzavřeno schopen přenést zatížení na sloupek bočnic. Obě spojení však selhala v důsledku zlomeniny základního kovu sloupce na špičce rohu svaru (obrázek 3). Toto křehké selhání při rotacích 0,4 rad. a 0,5 rad., respektive potvrdilo, že přímo svařované spoje neposkytují vhodné chování pro seismické aplikace.

obrázek 3. Fotografie roztříštěné (obrázek vlevo) bezkonkurenční a (obrázek vpravo) uzavřeno nevyztužené připojení sloupec zobrazen horizontální a paprsek ukázaly, vertikální

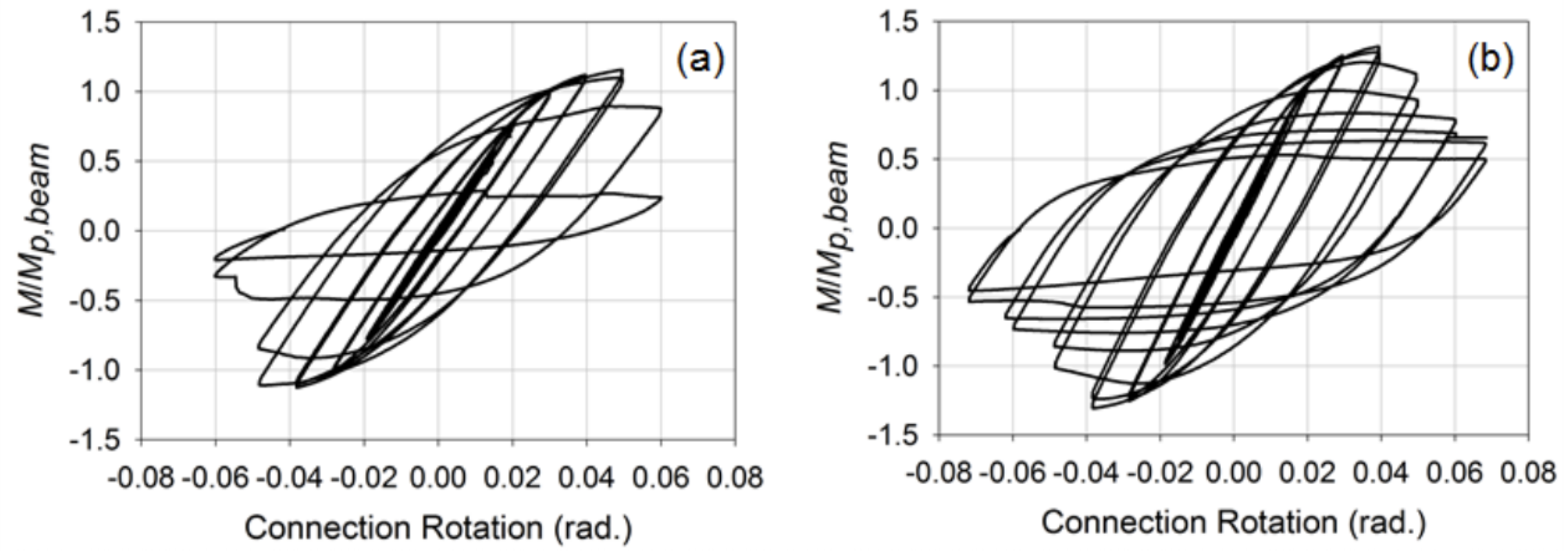
zesílené spoje pak byly vyvinuty s ohledem na skrz desku a vnější membrány desky, které jsou často používány v široké pásnice nosníku-k-HSS sloupci připojení s cílem poskytnout lepší mechanismus pro přenos napětí a kompresní síly na bočnici sloupec a minimalizovat stres koncentrace umístěny na svary. Pro tato spojení byly nosníky členy HSS 12x8x3/8 (β = 0,8). Informace o konkrétním postupu použitém k návrhu a detailu těchto spojení lze nalézt v Fadden and McCormick (2014b)a Fadden et al. (2015). Pod stejné zatížení jako nevyztužené připojení, připojení ukázala stabilnější chování s plastovým závěsem dochází daleko od kolony tvář na konci prostřednictvím nebo vnější membránový talíř (Obrázek 4). Oba spoje také dokázaly dosáhnout 0,4 rad. otáčení před podstoupením lokálního vzpěru, což mělo za následek degradaci momentové kapacity. Zlomenina se však iniciovala v rohu paprsku HSS v důsledku cyklování při velkých úrovních rotace 0,7 rad. Srovnání normalizovaných křivek momentové rotace pro sladěné a vnější membránové deskové spoje je vidět na obrázku 5. Celkově, zesílená spojení ukázala příslib pro použití systémů seismických momentů HSS-to-HSS, ale je třeba více práce, aby se tato spojení posunula k případné předkvalifikaci.

AISC. (2010). „Seismická ustanovení pro konstrukční ocelové budovy“. ANSI / AISC 341-10. Americký institut ocelové konstrukce, Chicago, IL.

AISC. (2010). „Specifikace pro konstrukční ocelové budovy“. ANSI / AISC 360-10. Americký institut ocelové konstrukce, Chicago, IL.

AWS. (2010). „Strukturální Svařovací Kód“. ANSI / AWS D1. 1, American Welding Society, Miami, FL.

Fadden, F. a McCormick, J. (2014a). „Model konečných prvků cyklického ohybového chování dutých konstrukčních částí“. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. and McCormick, J. (2014b). „HSS-to-HSS seismic Moment Connection Performance and Design“. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., and McCormick, J. (2015). „Cyklické testování svařovaných HSS-to-HSS momentových spojení pro seismické aplikace“. Asce Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J. E. M. a Redwood, R. G. (1966). „Návrh spojů do boxových sekcí“. Instituce stavebních Inženýrů, Konferenci na Průmyslové Budovy a stavební Inženýr, Ústav stavební Inženýři, Londýn.

Korol, R. M., El-Zanaty, M., a Brady, F. J. (1977). „Nerovnoměrné šířky spojů čtvercových dutých profilů ve Vierendeelových Vaznících“. Canadian Journal of Civil Engineering, 4, 190-201.

Packer, J. a. (1993). „Momentové spojení mezi pravoúhlými dutými úseky“. Journal of Constructional Steel Research, 25, 63-81.

Packer, J. a., Wardenier, J., Zhao, X-L, van der Vegte, G. J. a Kurobane, y. (2010). Design Guide 3: pro pravoúhlé duté sekce (RHS) spoje pod převážně statickým zatížením 2.vydání. CIDECT, Kanada.

Wardenier, J. (1982). „Duté Průřezové Spoje“. Delft University Press, Delft, Nizozemsko.

září 2016

Stáhnout PDF